比特排序算法

在本文中，我们将讨论比特排序算法。比特排序是一种并行排序算法，需要进行 O(n²log n) 次比较。尽管与其他任何流行排序算法相比，比较次数更多，但它在并行实现方面表现更好，因为元素的比较是按照预定义的序列进行的，该序列不依赖于被排序的数据。预定义的序列称为比特序列。

要理解比特排序，我们首先需要理解比特序列。

在比特序列中，元素首先按升序排列，然后在某个特定索引之后，它们开始下降。

如果存在一个索引 i，使得 -，则称数组 A[0…i…n-1] 为比特数组。

其中，0 ≤ i ≤ n-1。

在直接转向比特排序算法之前，请先理解如何将任何随机序列转换为比特序列。

如何将随机序列转换为比特序列？

考虑一个包含 n 个元素的序列 A[ 0 ... n-1]。首先，使用序列中的 4 个元素开始构建比特序列。将前 2 个元素按升序排序，将后 2 个元素按降序排序，然后将这对元素连接起来形成一个 4 个元素的比特序列。重复此过程，直到处理完所有元素对，直到我们得到一个比特序列。

让我们通过一个例子来理解将随机序列转换为比特序列的过程。

假设数组的元素是 - {30, 70, 40, 80, 60, 20, 10, 50}

转换后，我们将得到的比特序列是 -

30, 40, 70, 80, 60, 50, 20, 10

现在，让我们来看执行比特排序的步骤。

执行比特排序的步骤

执行比特排序的步骤如下所示 -

1. 第一步，我们必须从给定的随机序列创建比特序列，就像我们上面所做的那样。这被认为是过程的第一步。完成此步骤后，我们将得到一个序列，其中前半部分的元素按升序排列，而后半部分的元素按降序排列。
2. 现在，在第二步中，我们必须将前半部分与前半部分中的第一个元素进行比较，将前半部分与前半部分中的第二个元素进行比较，依此类推。在这里，如果我们发现后半部分的任何元素小于前半部分的对应元素，我们就需要交换它们。
3. 在执行上述步骤后，我们得到前半部分的所有元素都小于后半部分的所有元素。比较和交换的结果是两个长度为 n/2 的序列。对每个序列递归地重复第二步中执行的过程，直到我们得到一个长度为 n 的单个排序序列。

现在，让我们通过一个例子来看比特排序的整个过程。通过一个例子更容易理解比特排序，因为它使解释更清晰、更容易。

在下面的例子中，我们使用了上面从随机序列创建的比特序列。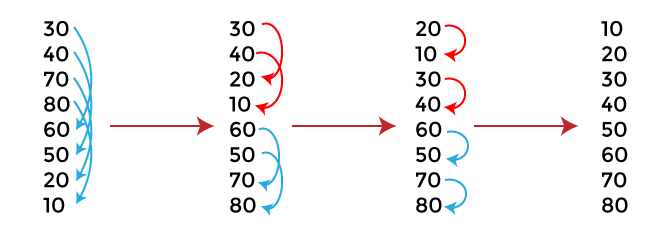

现在，给定的数组已完全排序。

比特排序复杂度

现在，让我们看看比特排序在最佳情况、平均情况和最坏情况下的时间复杂度。我们还将查看比特排序的空间复杂度。

1. 时间复杂度

比特排序的时间复杂度在所有三种情况下都是O(log² n)。

2. 空间复杂度

• 比特排序的空间复杂度是O(n log²n)。

比特排序的实现

现在，让我们看看不同编程语言中比特排序的程序。

程序：编写一个 C 语言程序来实现比特排序。

输出

执行上述代码后，输出将是 -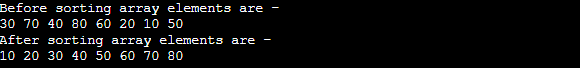

说明

在上面的代码中，我们创建了一个名为 exchange() 的函数。该函数接受 4 个参数。借助此函数，我们可以根据提供的位置交换元素。之后，我们创建了另一个名为 merge() 的函数。该函数也接受 4 个参数。借助此数组，我们可以合并两个子数组。在内部，此函数调用 exchange()。之后，我们创建了 bitonicSort()。借助此函数，我们实现了比特排序算法。此函数在内部调用 merge()。然后，我们创建了 sort()，它作为包装函数调用 bitonicSort() 来排序给定的数组。然后，我们创建了 print() 来打印排序后的数组。整个逻辑是用 C 语言编写的。

程序：编写一个 C++ 程序来实现比特排序。

输出

执行上述代码后，输出将是 -

说明

提供的 C++ 代码提供了一组用于实现比特排序算法的函数。首先，`exchange()` 函数方便地根据指定位置交换元素。接下来，`merge()` 函数用于合并两个子数组，内部使用 `exchange()` 函数。`bitonicSort()` 函数执行比特排序算法，并利用 `merge()` 函数。最后，`sort()` 函数通过调用 `bitonicSort()` 来排序给定的数组。最后，`print()` 函数负责清晰地显示排序后的数组。这些函数协同工作，以高效地在 C++ 中实现比特排序算法。

程序：编写一个 C# 程序来实现比特排序。

输出

执行上述代码后，输出将是 -

说明

提供的 C# 代码提供了一个比特排序算法的全面实现。它包含几个函数

`exchange()` 函数方便地根据提供的位置交换元素。`merge()` 函数合并两个子数组，并在内部使用 `exchange()` 函数。核心算法封装在 `bitonicSort()` 函数中，该函数递归地调用 `merge()` 函数。包含一个包装函数 `sort()` 来启动排序过程。最后，`print()` 函数负责整齐地显示排序后的数组。

这种有组织的结构有助于在 C# 中创建清晰有效的比特排序算法实现。

程序：编写一个 Java 程序来实现比特排序。

输出

执行上述代码后，输出将是 -

说明

提供的 Java 代码提供了一个比特排序算法的结构化实现。它首先定义了一个名为 `exchange()` 的函数，该函数根据给定位置方便地交换元素。接下来，引入了 `merge()` 函数，该函数接受四个参数来合并两个子数组，并在内部调用 `exchange()` 函数。算法的核心在于 `bitonicSort()` 函数，该函数递归地调用 `merge()`。然后创建了一个包装函数 `sort()`，通过在给定数组上调用 `bitonicSort()` 来启动排序过程。最后，创建了 `print()` 函数以整洁的方式显示排序后的数组。这种有组织的结构确保了在 Java 中实现比特排序算法的清晰度和效率。

比特排序算法的优点

使用比特排序有一些好处。它们如下。

1. 这种排序技术非常适合并行机器。
2. 比特排序算法简单易懂且易于实现。
3. 它的时间复杂度为 OO(nlogn)，与合并排序和其他高效排序算法相似。

比特排序算法的缺点

但是，了解比特排序的局限性很重要。它们如下。

1. 比特排序不是稳定的排序算法，这意味着它不能保证在排序数组中相似元素的顺序会得到保留。
2. 比特排序不是就地排序算法，这意味着需要额外的空间来对数据进行排序。
3. 它不像快速排序和合并排序等其他排序算法那样被广泛使用，因为它在顺序机器上的效率较低。

所以，这就是关于本文的全部内容。希望本文能对您有所帮助并提供信息。