选择排序算法（附带Python/Java/C/C++程序）

在选择排序中，在每次遍历中都会从未排序的数组元素中选择最小值，并将其插入到数组的适当位置。它也是最简单的算法。它是一种原地比较排序算法。

在此算法中，数组分为两部分；第一部分是已排序部分，另一部分是未排序部分。最初，数组的已排序部分为空，未排序部分是给定的数组。已排序部分放在左侧，未排序部分放在右侧。

选择排序通常在以下情况使用：

• 要排序的数组很小
• 交换成本不重要
• 必须检查所有元素

现在，让我们看看选择排序的算法。

算法

选择排序算法的步骤

步骤 1：找到最小元素并将其与输入数组的第一个元素交换。如果第一个元素是最小的，则无需交换。

步骤 2：从剩余元素中找到最小元素（第二个最小元素）并将其与第二个元素交换。同样，如果第二个最小元素是数组的第二个元素，则此处也无需交换。

步骤 3：对输入数组的剩余元素重复此过程，直到所有元素都达到正确位置。

选择排序算法的工作原理

现在，让我们看看选择排序算法的工作原理。

为了理解选择排序算法的工作原理，我们取一个未排序的数组。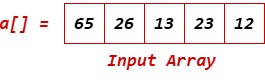

从左到右遍历数组。因此，我们遇到 65 作为当前元素。现在，从数组中找到最小的元素。我们看到 12 是最小的元素。

现在，将最小元素与当前元素交换。因此，最小元素在已排序数组中找到当前位置。

再次，找到下一个当前元素，即 26。同时，在数组的剩余元素中寻找最小的元素（总体而言第二个最小的元素）。我们看到最小的元素是 13。将 26 与 13 交换。

此时，数组的两个最小元素已放置在正确位置。现在，我们再次执行相同的过程，即从剩余元素中找到最小元素并与当前元素交换。我们发现最小元素是 23，当前元素是 26。因此，交换后，我们得到以下结果。

再次，重复相同的过程。此时，我们发现最小元素和当前元素相同。因此，无需交换。因此，我们已经排序了数组的四个元素。现在，我们移动到下一个元素。

在这里，我们也看到最小元素和当前元素相同。因此，无需交换。因此，我们已排序数组的所有元素。

选择排序在Python/Java/C/C++/C#中的实现

• Python
• Java
• C
• C++
• C#

输出

Before sorting array elements are: 
65 26 13 23 12 
After sorting array elements are: 
12 13 23 26 65 

复杂度分析

现在，让我们看看选择排序在最好情况、平均情况和最坏情况下的时间复杂度。我们还将看到选择排序的空间复杂度。

时间复杂度

最好情况复杂度：当不需要排序时发生，即数组已经排序。选择排序的最好情况时间复杂度是 O(n²)。

平均情况复杂度：当数组元素以混乱的顺序排列时发生，既不是完全升序也不是完全降序。选择排序的平均情况时间复杂度是 O(n²)。

最坏情况复杂度：当需要按逆序排序数组元素时发生。这意味着我们必须按升序排序数组元素，但其元素是降序排列的。选择排序的最坏情况时间复杂度是 O(n²)。

空间复杂度

选择排序的空间复杂度是 O(1)。这是因为在选择排序中，交换需要一个额外的变量。

选择排序算法的应用

1. 借助这种排序算法，我们可以对小班级学生的成绩或姓名进行排序。
2. 我们还可以按创建日期或大小在目录中组织文件。
3. 此外，借助此算法，我们可以按升序或降序排列一副扑克牌。
4. 我们还可以按价格在小型电子商务商店中排列商品列表。

选择排序算法的优点

使用选择排序有一些好处。它们如下所示。

1. 这种排序技术非常简单，易于理解和实现。
2. 它对小型数据集或几乎排序的数据集也高效。
3. 在元素排序期间不需要额外的空间。

选择排序算法的缺点

使用选择排序也有一些限制。它们如下所示。

1. 这种排序技术对于大型数据集效率低下，最坏情况时间复杂度为 O(n^2)。
2. 选择排序有大量比较，这会使其在现代计算机上变慢。
3. 这是一种不稳定的排序算法。这里，不稳定性意味着它可能不会在输入数组中保持相等元素的相对顺序。

结论

选择排序的平均和最坏情况复杂度是 O(n²)，其中 n 是项目数。因此，它不适用于大型数据集。它是一种不稳定的算法。选择排序易于实现。