数据结构中的优先队列

优先队列是一种抽象数据类型，其行为类似于普通队列，但每个元素都有一定的优先级，即优先级最高的元素将首先出现在优先队列中。优先队列中元素的优先级将决定元素从优先队列中移除的顺序。

优先队列仅支持可比较的元素，这意味着元素按升序或降序排列。

例如，假设我们有一些值，如 1、3、4、8、14、22 插入到优先队列中，值的排序是从小到大。因此，数字 1 将具有最高优先级，而 22 将具有最低优先级。

优先队列的特点

优先队列是队列的扩展，具有以下特点

• 优先队列中的每个元素都与某个优先级相关联。
• 优先级较高的元素将在优先级较低的元素之前被删除。
• 如果优先队列中的两个元素具有相同的优先级，它们将使用 FIFO 原则进行排列。

让我们通过一个例子来理解优先队列。

我们有一个包含以下值的优先队列

1, 3, 4, 8, 14, 22

所有值都按升序排列。现在，我们将观察执行以下操作后优先队列会是什么样子

• poll(): 此函数将从优先队列中移除优先级最高的元素。在上面的优先队列中，元素 '1' 具有最高优先级，因此它将从优先队列中移除。
• add(2): 此函数将在优先队列中插入元素 '2'。由于 2 是所有数字中最小的元素，因此它将获得最高优先级。
• poll(): 它将从优先队列中移除元素 '2'，因为它具有最高优先级。
• add(5): 它将在 4 之后插入元素 5，因为 5 大于 4 且小于 8，所以它将在优先队列中获得第三高优先级。

优先队列的类型

优先队列有两种类型

• 升序优先队列： 在升序优先队列中，较低的优先级数字被赋予较高的优先级。例如，我们取 1 到 5 的数字，按升序排列为 1,2,3,4,5；因此，最小的数字，即 1，在优先队列中被赋予最高优先级。
  
• 降序优先队列： 在降序优先队列中，较高的优先级数字被赋予较高的优先级。例如，我们取 1 到 5 的数字，按降序排列为 5,4,3,2,1；因此，最大的数字，即 5，在优先队列中被赋予最高优先级。
  

优先队列的表示

现在，我们将看看如何通过单向列表来表示优先队列。

我们将使用下表创建优先队列，其中 INFO 列表包含数据元素，PRN 列表包含 INFO 列表中每个数据元素的优先级数字，而 LINK 基本包含下一个节点的地址。

让我们一步一步地创建优先队列。

在优先队列中，较低的优先级数字被认为是较高的优先级，即，较低的优先级数字 = 较高的优先级。

步骤 1： 在列表中，较低的优先级数字是 1，其数据值为 333，因此它将插入到列表中，如下图所示

步骤 2： 插入 333 后，优先级数字 2 具有更高的优先级，与此优先级关联的数据值是 222 和 111。因此，这些数据将根据 FIFO 原则插入；因此 222 将首先添加，然后是 111。

步骤 3： 插入优先级 2 的元素后，下一个更高的优先级数字是 4，与优先级 4 关联的数据元素是 444、555、777。在这种情况下，元素将根据 FIFO 原则插入；因此，444 将首先添加，然后是 555，然后是 777。

步骤 4： 插入优先级 4 的元素后，下一个更高的优先级数字是 5，与优先级 5 关联的值是 666，因此它将插入到队列的末尾。

优先队列的实现

优先队列可以通过四种方式实现，包括数组、链表、堆数据结构和二叉搜索树。堆数据结构是实现优先队列最有效的方式，因此我们将在本主题中使用堆数据结构实现优先队列。现在，我们首先了解为什么堆在所有其他数据结构中是最有效的方式。

使用不同实现进行复杂度分析

什么是堆？

堆是一种基于树的数据结构，它形成一个完全二叉树，并满足堆属性。如果 A 是 B 的父节点，那么对于堆中的所有节点 A 和 B，A 相对于节点 B 是有序的。这意味着父节点的值可以大于或等于子节点的值，或者父节点的值可以小于或等于子节点的值。因此，我们可以说有两种类型的堆

• 最大堆： 最大堆是一种堆，其中父节点的值大于子节点的值。
  
• 最小堆： 最小堆是一种堆，其中父节点的值小于子节点的值。
  

两种堆都是二叉堆，因为它们都正好有两个子节点。

优先队列操作

我们可以在优先队列上执行的常见操作是插入、删除和窥视。让我们看看如何维护堆数据结构。

• 在优先队列中插入元素（最大堆）

如果我们在优先队列中插入一个元素，它将通过从上到下、从左到右查找来移动到空槽。

如果元素不在正确的位置，则将其与父节点进行比较；如果发现乱序，则交换元素。此过程继续进行，直到元素放置在正确的位置。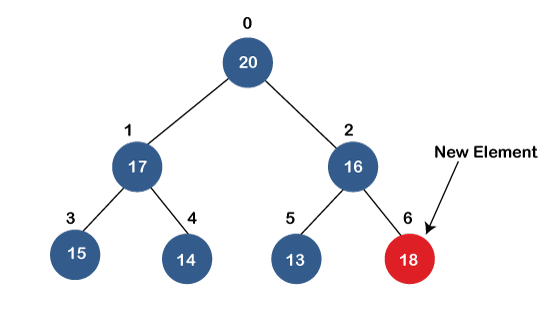

• 从优先队列中移除最小元素

正如我们所知，在最大堆中，最大元素是根节点。当我们移除根节点时，它会创建一个空槽。最后插入的元素将添加到此空槽中。然后，将此元素与子节点（即左子节点和右子节点）进行比较，并与两者中较小的一个进行交换。它不断向下移动树，直到堆属性恢复。

优先队列的应用

以下是优先队列的应用

• 它用于 Dijkstra 的最短路径算法。
• 它用于 Prim 算法
• 它用于数据压缩技术，如霍夫曼编码。
• 它用于堆排序。
• 它也用于操作系统，如优先级调度、负载均衡和中断处理。

使用二叉最大堆创建优先队列的程序。

在上面的程序中，我们创建了以下函数

• int parent(int i)： 此函数返回子节点（即 i）的父节点的索引。
• int left_child(int i)： 此函数返回给定索引（即 i）的左子节点的索引。
• int right_child(int i)： 此函数返回给定索引（即 i）的右子节点的索引。
• void moveUp(int i)： 此函数将使节点向上移动树，直到堆属性恢复。
• void moveDown(int i)： 此函数将使节点向下移动树，直到堆属性恢复。
• void removeMax()： 此函数移除优先级最高的元素。
• void insert(int p)： 它在优先队列中插入作为函数参数传递的元素。
• void delete(int i)： 它从给定索引的优先队列中删除元素。
• int get_Max()： 它返回优先级最高的元素，我们知道在最大堆中，根节点包含具有最大值和最高优先级的元素。
• int get_Min()： 它返回优先级最低的元素，我们知道在最大堆中，最后一个节点包含具有最小值和最低优先级的元素。

输出