后序遍历

在本文中，我们将讨论数据结构中的后序遍历。

线性数据结构，如栈、数组、队列等，只有一种遍历数据的方式。但在分层数据结构，如树中，有多种遍历数据的方式。因此，这里我们将讨论另一种遍历树数据结构的方式，即后序遍历。后序遍历是用于访问树中节点的遍历技术之一。它遵循左右根 (LRN) 原则。后序遍历用于获取树的后缀表达式。

执行后序遍历的步骤如下

• 通过递归调用后序函数遍历左子树。
• 通过递归调用后序函数遍历右子树。
• 访问当前节点的数据部分。

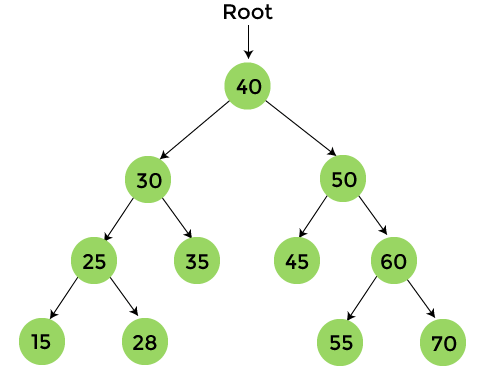
后序遍历技术遵循左右根策略。这里，左右根意味着首先遍历根节点的左子树，然后是右子树，最后遍历根节点。在这里，“后序”这个名称本身就表明树的根节点将在最后遍历。

算法

现在，让我们看看后序遍历的算法。

后序遍历示例

现在，让我们看一个后序遍历的例子。通过一个例子来理解后序遍历的过程会更容易。

黄色节点尚未访问。现在，我们将使用后序遍历来遍历上面树的节点。

• 这里，40 是根节点。我们首先访问 40 的左子树，即 30。节点 30 也将进行后序遍历。25 是 30 的左子树，因此也进行后序遍历。然后 15 是 25 的左子树。但 15 没有子树，所以打印 15 并转向 25 的右子树。
  
• 28 是 25 的右子树，它没有子节点。所以，打印 28。
  
• 现在，打印 25，25 的后序遍历完成。
  
• 接下来，转向 30 的右子树。35 是 30 的右子树，它没有子节点。所以，打印 35。
  
• 之后，打印 30，30 的后序遍历完成。至此，给定二叉树的左子树遍历完成。
  
• 现在，转向 40 的右子树，即 50，它也将进行后序遍历。45 是 50 的左子树，它没有子节点。所以，打印 45 并转向 50 的右子树。
  
• 60 是 50 的右子树，它也将进行后序遍历。55 是 60 的左子树，它没有子节点。所以，打印 55。
  
• 现在，打印 70，它是 60 的右子树。
  
• 现在，打印 60，60 的后序遍历完成。
  
• 现在，打印 50，50 的后序遍历完成。
  
• 最后，打印 40，它是给定二叉树的根节点，节点 40 的后序遍历完成。
  

后序遍历后我们将得到的最终输出是 -

{15, 28, 25, 35, 30, 45, 55, 70, 60, 50, 40}

后序遍历的复杂度

后序遍历的时间复杂度是 O(n)，其中 'n' 是二叉树的大小。

而如果我们在不考虑函数调用栈大小的情况下，后序遍历的空间复杂度是 O(1)。否则，后序遍历的空间复杂度是 O(h)，其中 'h' 是树的高度。

后序遍历的实现

现在，让我们看看后序遍历在不同编程语言中的实现。

程序： 编写一个程序以 C 语言实现后序遍历。

输出

程序： 编写一个程序以 C++ 实现后序遍历。

输出

程序： 编写一个程序以 C# 实现后序遍历。

输出

执行上述代码后，输出将是 -

程序： 编写一个程序以 Java 实现后序遍历。

输出

执行上述代码后，输出将是 -

所以，这就是关于本文的全部内容。希望本文能对您有所帮助并提供信息。