数据结构中的最优二叉搜索树

引言

在数据结构领域，搜索操作的效率至关重要。最优二叉搜索树（OBST）是一个满足这一需求的基本概念。OBST 是一种二叉搜索树，它能减少给定键集的典型搜索时间。这种树是使用复杂的算法和动态规划技术构建的，这些技术优化了结构以实现快速访问。

认识到树的结构可能会极大地影响搜索操作的性能，这导致了对最优二叉搜索树的需求。当某些键比其他键使用更频繁时，必须对其进行排列，以使平均搜索时间尽可能短。理想的二叉搜索树旨在通过将常用键放置在离根更近的位置来利用访问概率，从而缩短平均搜索时间。

二叉搜索树（BST）——OBST 的基础

在深入了解 OBST 的细节之前，让我们回顾一下二叉搜索树的基础知识。二叉搜索树中的每个节点最多可以有两个子节点，通常称为右子节点和左子节点。BST 的主要特征是其左子树中的每个元素都小于其右子树中的每个元素，反之亦然。

BST 因其固有的排序特性而适用于有效的搜索操作。然而，节点在树内的精确配置将影响整体性能。在最坏的情况下，倾斜的树将导致退化树，其搜索时间与节点数成正比。

动态规划方法

OBST 是使用动态规划策略构建的。基本概念是将问题分解为更小的部分，解决每个部分，然后整合解决方案以创建最佳解决方案。

子问题识别

• 通过考虑所有潜在的子树来定义子问题。
• 将每个键视为给定键集的根，然后将剩余的键分为左子树和右子树。

递推关系

• 创建递归关系，其中最佳二叉搜索树的成本以其每个子树的成本表示。
• 成本包括左右子树的成本以及与键相关的概率总和。

自底向上解决方案构建

• 使用动态规划表来跟踪中间结果。
• 通过从小子树逐步构建，可以获得理想的二叉搜索树。
• 使用递归关系填充表，直到找到精确的解决方案。

算法复杂度

使用动态规划创建 OBST 的时间复杂度为 O(n³)，其中“n”是键的总数。这是因为需要考虑所有潜在的子树并评估每个子树的所有潜在根。尽管这可能看起来计算成本很高，但搜索操作中获得的生产力验证了构建理想树的努力。

代码

输出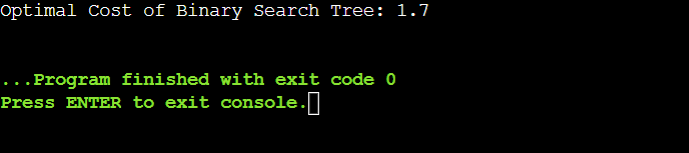

结论

一种简化动态数据集搜索过程的有效方法是使用最优二叉搜索树。OBST 通过根据访问概率智能地组织常用键，确保它们离根更近，从而减少平均搜索时间。动态规划方法系统地创建了一个理想的二叉搜索树，将问题分解为更小、更易于管理的问题，并逐步构建到理想的答案。尽管算法复杂度可能看起来令人生畏，但提高的搜索效率证明了计算开销是合理的。

对于寻求创建高性能系统的计算机科学家和软件工程师来说，理解和使用最优二叉搜索树至关重要。随着技术的发展，高效的算法和数据结构对于软件开发至关重要，因此 OBST 的研究是计算机科学领域一项有益的努力。