稀疏矩阵 (数据结构)

2025 年 4 月 21 日 | 阅读 7 分钟

在本文中，我们将讨论稀疏矩阵。

首先，让我们简要介绍一下矩阵。

什么是矩阵？

矩阵可以定义为具有 'm' 行和 'n' 列的二维数组。一个有 m 行 n 列的矩阵称为 m × n 矩阵。它是一组按水平或垂直排列的条目（数字）。

例如 -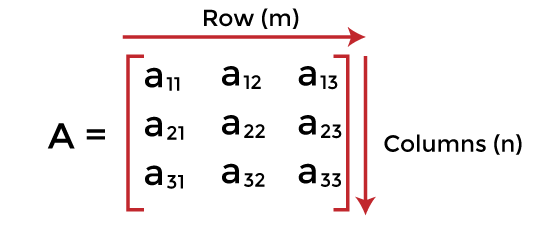

什么是稀疏矩阵？

稀疏矩阵是其大部分元素都为零的矩阵。换句话说，稀疏矩阵可以定义为零元素数量多于非零元素数量的矩阵。

现在，问题来了：我们也可以使用普通矩阵来存储元素，那么为什么还需要稀疏矩阵呢？

如果我们能用普通矩阵存储元素，为什么还需要稀疏矩阵？

使用稀疏矩阵有以下好处：

存储 - 我们知道稀疏矩阵中的零元素多于非零元素，因此可以节省内存来存储元素。它只计算非零元素。

计算时间：在稀疏矩阵中搜索时，我们只需要遍历非零元素，而不是遍历整个稀疏矩阵。通过逻辑设计数据结构来遍历非零元素，可以节省计算时间。

稀疏矩阵的表示

现在，让我们看看稀疏矩阵的表示。稀疏矩阵中的非零元素可以使用三元组（行、列和值）来存储。稀疏矩阵有两种表示方法，列出如下：

数组表示
链表表示

稀疏矩阵的数组表示

使用二维数组表示稀疏矩阵会导致大量内存浪费。这是因为矩阵中的零没有用处，所以将零与非零元素一起存储是浪费内存。为了避免这种浪费，我们可以只存储非零元素。如果只存储非零元素，则可以减少遍历时间和存储空间。

在稀疏矩阵的二维数组表示中，使用了三个字段，分别命名为：

行 - 指示矩阵中非零元素所在行的索引。
列 - 指示矩阵中非零元素所在列的索引。
值 - 指示位于 (行, 列) 索引处的非零元素的值。

示例 -

让我们通过下面的例子来理解稀疏矩阵的数组表示：

考虑稀疏矩阵 -

在上图中，我们可以观察到一个 5x4 的稀疏矩阵，包含 7 个非零元素和 13 个零元素。上述矩阵占用 5x4 = 20 个内存空间。增加矩阵的大小会增加浪费的空间。

上述矩阵的表格表示如下：

在上述结构中，第一列代表行，第二列代表列，第三列代表非零值。表格的第一行代表三元组。第一个三元组表示值 4 存储在第 0 行和第 1 列。类似地，第二个三元组表示值 5 存储在第 0 行和第 3 列。以此类推，所有三元组都表示矩阵中非零元素的存储位置。

表格的大小取决于给定稀疏矩阵中非零元素的总数。上面的表格占用了 8x3 = 24 个内存空间，这比稀疏矩阵占用的空间还要多。那么，使用稀疏矩阵的好处是什么？考虑一个 8*8 的矩阵，其中只有 8 个非零元素，那么稀疏矩阵占用的空间将是 8*8 = 64，而使用三元组表示的表格占用的空间将是 8*3 = 24。

稀疏矩阵数组表示的实现

现在，让我们看看 C 语言中稀疏矩阵数组表示的实现。

在下面的程序中，我们将展示存储在数组中的稀疏矩阵非零元素的表格表示。

示例

#include <stdio.h>
int main()
{
    // Sparse matrix having size 4*5
    int sparse_matrix[4][5] =
    {
        {0 , 0 , 6 , 0 , 9 },
        {0 , 0 , 4 , 6 , 0 },
        {0 , 0 , 0 , 0 , 0 },
        {0 , 1 , 2 , 0 , 0 }
    };
   // size of matrix
    int size = 0;
    for(int i=0; i<4; i++)
    {
        for(int j=0; j<5; j++)
        {
            if(sparse_matrix[i][j]!=0)
            {
                size++;
            }
        }
    }
   // Defining final matrix
    int matrix[3][size]; 
     int k=0;
   // Computing final matrix
    for(int i=0; i<4; i++)
    {
        for(int j=0; j<5; j++)
        {
            if(sparse_matrix[i][j]!=0)
            {
                matrix[0][k] = i;
                matrix[1][k] = j;
                matrix[2][k] = sparse_matrix[i][j];
                k++;
            }
      }
    }
   // Displaying the final matrix
    for(int i=0 ;i<3; i++)
    {
        for(int j=0; j<size; j++)
        {
            printf("%d ", matrix[i][j]);
            printf("\t");
        }
        printf("\n");
    }
    return 0;
}

编译并运行

输出

在输出中，表格的第一行表示值的行位置，第二行表示值的列位置，第三行表示值本身。

在下面的截图中，第一列的值为 0、2 和 6，表示值 6 存储在第 0 行和第 2 列。

稀疏矩阵的链表表示

在链表表示中，链表数据结构用于表示稀疏矩阵。使用链表表示稀疏矩阵的优点是，在链表中插入或删除节点的复杂度比数组小。

与数组表示不同，链表表示中的节点包含四个字段。链表的四个字段如下：

行 - 指示非零元素所在行的索引。
列 - 指示非零元素所在列的索引。
值 - 指示位于 (行, 列) 索引处的非零元素的值。
下一个节点 - 存储下一个节点的地址。

稀疏矩阵链表表示的节点结构如下图所示：

示例 -

让我们通过下面的例子来理解稀疏矩阵的链表表示：

考虑稀疏矩阵 -

在上图中，我们可以观察到一个 4x4 的稀疏矩阵，包含 5 个非零元素和 11 个零元素。上述矩阵占用 4x4 = 16 个内存空间。增加矩阵的大小会增加浪费的空间。

上述矩阵的链表表示如下：

在上图中，稀疏矩阵以链表的形式表示。在节点中，第一个字段表示行的索引，第二个字段表示列的索引，第三个字段表示值，第四个字段包含下一个节点的地址。

在上图中，链表第一个节点的第一个字段包含 0，表示第 0 行；第二个字段包含 2，表示第 2 列；第三个字段包含 1，即非零元素。因此，第一个节点表示元素 1 存储在给定稀疏矩阵的第 0 行第 2 列。以此类推，所有节点都表示稀疏矩阵的非零元素。

稀疏矩阵链表表示的实现

现在，让我们看看 Java 中稀疏矩阵链表表示的实现。

示例

class Node {
int row;
int col;
int value;
Node next;
Node(int r, int c, int val) 
{ row = r; col = c; this.value = val; }
}
public class Sparse{
public static void main(String[] args)
{
/*Assume a 4x4 sparse matrix */
int sparseMatrix[][] = {
{0, 0, 1, 2},
{3, 0, 0, 0},
{0, 4, 5, 0},
{0, 6, 0, 0}
};
Node start = null; /*Start with the empty list*/
Node tail = null;
int k = 0;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
{
if (sparseMatrix[i][j] != 0) /*Pass only non-zero values*/
{
Node temp = new Node(i, j, sparseMatrix[i][j]);
temp.next = null;
if(start == null){
start = temp;
tail=temp;
}
else{
tail.next = temp;
tail = tail.next;
}
}
}
Node itr = start;
while(start != null){
System.out.println(start.row  + " " + start.col + " " + start.value);
start = start.next;
}
}
}

编译并运行

输出

输出中的每一行代表链表的一个节点。在下面截屏的每一行中，第一个元素表示非零元素的行索引位置，第二个元素表示非零元素的列索引位置，第三个元素表示非零元素本身。