大分区的数量

2025年2月7日 | 阅读 12 分钟

问题陈述

在此问题陈述中，我们给定一个包含正整数的数组 nums 和一个整数 k。将数组划分为两个有序组，使得每个元素恰好属于一个组。如果每组元素的和都大于或等于 k，则称该划分是“great”的。返回不同“great”划分的数量。由于答案可能非常大，请对 10^9 + 7 取模返回。如果两个划分中某个元素 nums[i] 所在的组不同，则这两个划分被视为不同。

示例 1

输入： nums = [1,2,3,4], k = 4

输出 6

说明

划分 1：组 1 = [1, 2, 3]，组 2 = [4]。 (两组元素的和 = 6 > 4)

划分 2：组 1 = [1, 3]，组 2 = [2, 4]。 (两组元素的和 = 4 = 4)

划分 3：组 1 = [1, 4]，组 2 = [2, 3]。 (两组元素的和 = 5 > 4)

划分 4：组 1 = [2, 3]，组 2 = [1, 4]。 (两组元素的和 = 5 > 4)

划分 5：组 1 = [2, 4]，组 2 = [1, 3]。 (两组元素的和 = 6 > 4)

划分 6：组 1 = [4]，组 2 = [1, 2, 3]。 (两组元素的和 = 7 > 4)

共有 6 种划分，其中每组元素的和都大于或等于 4。因此，此示例的输出是 6。

示例 2

输入： nums = [3,3,3], k = 4

输出 0

说明

划分 1：组 1 = [3, 3]，组 2 = [3]。 (两组元素的和 = 6 > 4)

划分 2：组 1 = [3]，组 2 = [3, 3]。 (两组元素的和 = 6 > 4)

这些划分都满足每组元素总和大于或等于 4 的要求。但由于它们包含相同的组件，因此划分不是唯一的。因此，在此情况下，输出为 0。

使用背包问题的 Java 方法

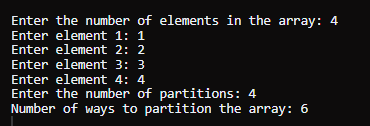
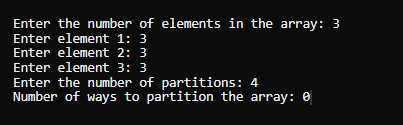import java. util.Scanner; 
public class Solution {
    // Function to count partitions
    public int countPartitions(int[] A, int k) {
        long mod = (long)1e9 + 7, total = 0, res = 1;
        long[] dp = new long[k];
        dp[0] = 1; // Base case
        // Traverse through the array elements
        for (int a: A) {
            // Update the dp array using dynamic programming
for (int i = k - 1 - a; i >= 0; --i) {
dp[i + a] = (dp[i + a] + dp[i]) % mod;
            }
            // Update the result
res = res * 2 % mod;
            // Calculate the total sum of elements
total += a;
        }
        // Update the result based on total sum and dp array
        for (int i = 0; i < k; ++i) {
res -= total - i < k ? dp[i] : dp[i] * 2;
        }
        // Return  final result
        return (int)((res % mod + mod) % mod);
    }
    public static void main(String[] args) {
Scanner scanner = new Scanner(System.in); 
System.out.print("Enter the number of elements in the array: ");
        int n = scanner.nextInt(); 
        int[] A = new int[n];
        for (int i = 0; i < n; i++) {
System.out.print("Enter element " + (i + 1) + ": ");
A[i] = scanner.nextInt(); 
        }
System.out.print("Enter the number of partitions: ");
        int k = scanner.nextInt();
scanner.close();
Solution solution = new Solution();
        int result = solution.countPartitions(A, k); 
System.out.println("Number of ways to partition the array: " + result);
    }
}

输出

代码解释

初始化

指定 10^9 + 7 作为模值初始化。
初始化 total 以存储数组中元素的总和。
将 res 初始化为 1 以保存结果。
建立一个大小为 k 的 DP 数组 dp，用于存储达到每个和的方法数。

动态规划

遍历数组 A 中的每个元素 a。
对于每个元素 a，使用动态规划更新 DP 数组，以计算从 0 到 k - 1 的每个和的方法数。
通过从 k - 1 - a 到 0 向后更新 DP 数组的值来实现。对于每个索引 i，通过将 dp[i] 添加到 dp[i + a] 来更新 dp[i + a]。
确保所有计算都按模 mod 执行。

更新结果

在为每个元素实现 DP 数组后，将 res 变量乘以 2，然后取模 mod。
通过对每个元素求和来获取数组中元素的总和。

最终结果计算

逐一遍历 DP 数组的索引 i。
根据 DP 数组的值和总和调整 res。如果 total - i 小于 k，则从 res 中减去 dp[i]。否则，减去 dp[i] * 2。

返回结果

取模 mod 后返回最终结果。

时间复杂度

时间复杂度为 O(nk) 的算法将实现，其中 n 和 k 分别是输入数组 A 的长度和划分数。因此，当有超过 O(A) 个元素时，由于其中存在 O(n) 和 O(k) 次迭代的嵌套循环，以及一个扫描 A 的第 i 个元素的 dp 数组，时间复杂度为 O(n*k)。

空间复杂度

空间复杂度为 O(k)，因为算法使用大小为 k 的动态数组作为处理空间来存储每个可能和的划分数。此外，还存在一些常规的空间变量。

使用递归+记忆化的 Java 方法

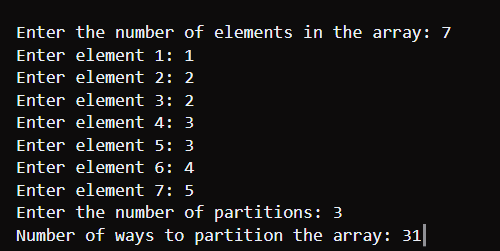
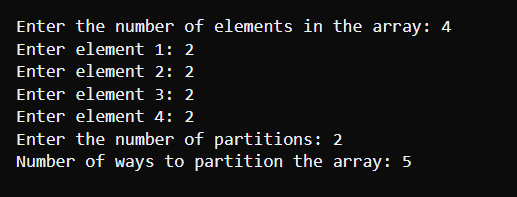import java. util.Arrays;
import java. util.Scanner; 
public class Solution {
    int mod = (int)1e9 + 7; 
    public int countPartitions(int[] nums, int k) {
        long sum = 0; 
for(int num : nums) sum += num; 
        // If  sum is less than twice the number of partitions, return 0
        if(sum < 2 * k) return 0; 
        int n = nums.length; 
        // set a memoization array.
int[][] memo = new int[n + 1][k + 1]; 
for(int[] row : memo) Arrays.fill(row, -1); 
        int notGreatPartitions = countPar(n, k, nums, memo); 
        int total = (int)(Math.pow(2, n) % mod); 
        return total - notGreatPartitions + (total < notGreatPartitions ? mod : 0);
    }
    private int countPar(int index, int k, int[] nums, int[][] memo) {
        // below is the base case
if(index == 0) return 2; 
        // If the result is already computed, return it from memoization array
if(memo[index][k] != -1) return memo[index][k]; 
        int pick = k > nums[index - 1] ? countPar(index - 1, k - nums[index - 1], nums, memo) : 0;
        int notPick = countPar(index - 1, k, nums, memo); 
        // Store the result in the memoization array and return
        return memo[index][k] = (pick + notPick) % mod;
    }
    public static void main(String[] args) {
        // We are creating a scanner class  for the input
Scanner scanner = new Scanner(System.in);
System.out.print("Enter the number of elements in the array: ");
        int n = scanner.nextInt(); 
        int[] A = new int[n];
        for (int i = 0; i < n; i++) {
System.out.print("Enter element " + (i + 1) + ": ");
A[i] = scanner.nextInt(); 
        }
System.out.print("Enter the number of partitions: ");
        int k = scanner.nextInt(); 
scanner.close();
Solution solution = new Solution();
        int result = solution.countPartitions(A, k); 
System.out.println("Number of ways to partition the array: " + result);
    }
}

输出

代码解释

初始化：

为常量 mod 指定模运算。
变量 sum 用于存储数组 nums 中所有元素的总和。
由于如果 total (sum) 小于 2 倍的划分数 (2 * k)，则不可能生成具有非零和的 k 个划分，因此相关函数返回 0。

记忆化数组

初始化大小为 (n + 1) x (k + 1) 的数组 memory 来存储每个子问题的结果。
所有数组元素都初始化为 -1，每个元素都表示该子问题的结果尚未计算。

递归函数 countPar

此特定函数以递归方式计算划分数。
它同时考虑两种情况：notPick（排除当前数字在划分中）和 selecting（包含它）。
如果当前数字等于剩余和（k > nums[index - 1]），则以减小的和递归执行 countPar。

主函数 countPartitions

算法从这个函数开始。
它使用递归函数 countPar 来获得划分的总数。
接下来，它使用公式 (Math.pow(2, n) % mod) 来确定可以生成的划分总数，即 2^n。
最后，它返回“非 great”划分的总数与所有可行划分的总数之间的差值，如果需要，则加上 mod 以确保结果为非负。

时间复杂度

算法的时间复杂度可以通过计算记忆空间分配的维度来获得，即 (n+1)*(k+1)，其中 n 是数组中的项目数，k 是差值。

空间复杂度

空间复杂度也是 O(n*k)，因为记忆化数组中的分配是输入大小，并且需要保留算法计数器。

使用制表的 Java 方法

import java. util.Scanner; 
public class Solution {
    public static void main(String[] args) {
Scanner scanner = new Scanner(System.in); 
System.out.print("Enter the number of elements in the array: ");
        int n = scanner.nextInt(); // Number of elements in the array
        int[] nums = new int[n];
        for (int i = 0; i < n; i++) {
System.out.print("Enter element " + (i + 1) + ": ");
nums[i] = scanner.nextInt(); 
        }
System.out.print("Enter the number of partitions: ");
        int k = scanner.nextInt(); 
scanner.close();
        int result = countPartitions(nums, k); 
System.out.println("Number of ways to partition the array: " + result); 
    }
        public static int countPartitions(int[] nums, int k) {
        int mod = (int) 1e9 + 7;
        long sum = 0;
        for (int num : nums) {
sum += num;
        }
        if (sum < 2 * k) {
return 0;
        }
        int n = nums.length; 
int[][] dp = new int[n + 1][k + 1]; 
        // Initialize the base case
        for (int target = 1; target <= k; target++) {
dp[0][target] = 2;
        }
        //We have to fill the dp table
        for (int index = 1; index <= n; index++) {
for (int target = 1; target <= k; target++) {
int pick = target > nums[index - 1] ? dp[index - 1][target - nums[index - 1]] : 0;
                int notPick = dp[index - 1][target]; 
dp[index][target] = (pick + notPick) % mod;
            }
        }
        int notGreatPartitions = dp[n][k];
        int total = (int) (Math.pow(2, n) % mod);
        return total - notGreatPartitions + (total < notGreatPartitions ? mod : 0);
    }
}

输出

代码解释

初始化

为了执行模运算，算法将 mod 变量的初始值设置为 10^9 + 7。
它计算并存储变量 sum，即数组 nums 中所有元素的总和。

基本情况检查

如果元素总和 (sum) 小于划分数 (2 * k) 的两倍，则不可能创建具有非零和的 k 个划分。在这种情况下，函数返回 0。

动态规划方法

使用大小为 (n + 1) x (k + 1) 的二维数组 dp 来存储子问题的中间结果。
dp[i][j] 表示将数组的前 i 个元素划分成恰好 j 个分区的数量。

基本情况初始化

对于每个目标分区 (target)，基本情况初始化为 2，表示两种可能性：当前分区为空或包含单个元素。

填充 DP 表

算法遍历数组中的每个元素和每个潜在的目标分区。
它考虑两种情况：a：选择（将当前元素包含在当前分区中）和不选择（notPick）。
基于这些实例，修改 dp[index][target] 的值。

计算总分区数

不符合“great”条件的划分数量（即不满足其和大于 0 的条件）存储在变量 notGreatPartitions 中。
使用公式 (2^n) % mod，变量 total 确定可能的分区总数。
最后，算法返回“非 great”划分的数量与潜在划分总数之间的差值。

时间复杂度

该解法的时间复杂度估计为 O(n * k)，其中 n 是输入数组的长度，k 是查询的数量。由于两个 for 循环分别遍历数组元素和所有可能的和，因此上述条件成立。

空间复杂度

空间复杂度也为 O(n*k)，这一点也很重要。原因之一可能是评估方法是二维的，并且该数组用于显示每个索引和目标和的组合。此外，还为数组元素的总和等值和其他类似详细信息进行了空间预留。

使用制表法的 Java 方法 - 空间优化

import java. util.Scanner; 
public class Main {
    public static void main(String[] args) {
        // Create a Scanner object to read input from the console
        Scanner scanner = new Scanner(System.in); 
        // Prompt user for input
System.out.print("Enter the number of elements in the array: ");
        int n = scanner.nextInt(); // Number of elements in the array
        int[] nums = new int[n];
        for (int i = 0; i < n; i++) {
System.out.print("Enter element " + (i + 1) + ": ");  
nums[i] = scanner.nextInt(); // Input array elements
        }
System. out.print("Enter the number of partitions: ");
        int k = scanner.nextInt(); // Number of partitions
        // Close the scanner object
scanner.close();
        // Create an instance of the Solution class
Solution solution = new Solution();
        // Call the countPartitions method and print the result
        int result = solution.countPartitions(nums, k); 
System.out.println("Number of ways to partition the array: " + result);
    }
}
class Solution {
    // Function to count partitions
    public int countPartitions(int[] nums, int k) {
        int mod = (int) 1e9 + 7;
        long sum = 0;
        // Calculate the sum of the array elements
        for (int num: nums) 
sum += num;
        // If the total sum is less than 2 times k, return 0
        if (sum < 2 * k) 
return 0;
        int n = nums.length;
        // Initialize the previous array with 2 for all target sums
        int[] prev = new int[k + 1];
        for (int target = 1; target <= k; target++)
            prev[target] = 2;
        // Iterate over the array elements
        for (int index = 1; index <= n; index++) {
            // Initialize the current array
int[] curr = new int[k + 1]; 
for (int target = 1; target <= k; target++) {
// Calculate the number of partitions with and without picking the current element
int pick = target > nums[index - 1] ? prev[target - nums[index - 1]] : 0; 
int notPick = prev[target]; 
// Update the current array with the sum of partitions
curr[target] = (pick + notPick) % mod;
            }
            // Update the previous array with the current array
prev = curr;
        }
        // Get the number of partitions without great partitions
        int notGreatPartitions = prev[k];
        // Calculate the total number of partitions
        int total = (int) (Math.pow(2, n) % mod);
        // Calculate the final result
        return total - notGreatPartitions + (total < notGreatPartitions ? mod : 0);
    }
}

输出

代码解释

初始化

为了处理模运算，算法将 mod 变量初始化为 10^9 + 7。它计算并存储变量 sum，即数组 nums 中所有元素的总和。
基本情况验证：算法确定 sum（所有元素总和）是否小于 2 * k。
如果是这样，则无法创建具有非零和的 k 个分区。在这种情况下，函数返回 0。

动态规划方法

该算法使用动态规划来找到解决该问题更有效的方法。
它维护两个数组：curr 和 prev。curr[target] 基于 prev 数组更新，prev[target] 表示使用直到前一个索引的元素形成和为 target 的分区数。

基本情况初始化

对于每个目标分区 (target)，基本情况初始化为 2，表示两种可能性：当前分区为空或包含单个元素。

填充 DP 表

算法遍历数组中的每个元素以及每个可能的 target 分区。
在每一步，它考虑两种情况：
- 包含当前元素 (pick)：它还使用 prev 数组计算具有和 target - nums[index - 1] 的分区数。
- 不包含当前元素 (notPick)：它从 prev 数组中检索具有和 target 的分区数。
curr[target] 的值通过 pick 和 notPick 的和（取模 mod）进行更新。

计算总分区数

该算法使用公式 (2^n)% mod 来确定总分区数 (total)。

通过获得 prev[k] 的值，它确定了“非 great”分区的数量 (notGreatPartitions)。

该过程最后返回 total 和 notGreatPartitions 之间的差值（取模 mod）。

时间复杂度

上述代码的时间复杂度为 O(n * k)，其中 n 是 nums 的长度，k 是给定的 targetSum。由于为了查找所需和而对数组元素进行嵌套循环，因此存在这种复杂度。

空间复杂度

空间复杂度为 O(k)，其中 k 是和。首先，我们有一个长度为 k 的额外数组，用于存储每个目标和的划分索引，这比存储大小为 n*k 的整个 dp 数组要节省得多。

下一主题精准 k 步到达位置的方法数

大分区的数量

问题陈述

示例 1

说明

示例 2

说明

使用背包问题的 Java 方法

代码解释

时间复杂度

空间复杂度

使用递归+记忆化的 Java 方法

代码解释

时间复杂度

空间复杂度

使用制表的 Java 方法

代码解释

时间复杂度

空间复杂度

使用制表法的 Java 方法 - 空间优化

代码解释

时间复杂度

空间复杂度

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

大分区的数量

问题陈述

示例 1

说明

示例 2

说明

使用背包问题的 Java 方法

代码解释

时间复杂度

空间复杂度

使用递归+记忆化的 Java 方法

代码解释

时间复杂度

空间复杂度

使用制表的 Java 方法

代码解释

时间复杂度

空间复杂度

使用制表法的 Java 方法 - 空间优化

代码解释

时间复杂度

空间复杂度

相关帖子

不相交集数据结构

构建堆的时间复杂度

数据结构中的老鼠进迷宫问题

二叉搜索树前序遍历的叶节点

以垂直顺序打印二叉树

AVL 树的平衡因子是什么

N 元树的序列化和反序列化

二进制链表的十进制等价物

查找两棵二叉树右视图和之间的绝对差值

动态规划 (DP) 在网格上

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器