二叉搜索树

在本文中，我们将讨论二叉搜索树。对于有技术背景的学生来说，本文将非常有用和信息丰富，因为它是他们课程中的一个重要主题。

在直接进入二叉搜索树之前，让我们先简要介绍一下树。

什么是树？

树是一种数据结构，用于以分层形式表示数据。它可以定义为一组称为节点的对象或实体，这些节点相互链接以模拟分层结构。树是一种非线性数据结构，因为树中的数据不是以线性或顺序方式存储的。

现在，让我们开始讨论二叉搜索树这个主题。

什么是二叉搜索树？

二叉搜索树遵循一定的顺序来组织元素。在二叉搜索树中，左子节点的值必须小于父节点，右子节点的值必须大于父节点。此规则递归地应用于根的左子树和右子树。

让我们通过一个例子来理解二叉搜索树的概念。

在上面的图中，我们可以看到根节点是40，左子树的所有节点都小于根节点，而右子树的所有节点都大于根节点。

同样，我们可以看到根节点的左子节点大于其左子节点，小于其右子节点。因此，它也满足二叉搜索树的属性。因此，我们可以说上图中的树是一棵二叉搜索树。

假设我们将上图中的节点35的值更改为55，请检查该树是否仍为二叉搜索树。

在上图中，根节点的值为40，它大于其左子节点30，但小于30的右子节点，即55。因此，上图不满足二叉搜索树的属性。因此，上图不是二叉搜索树。

二叉搜索树的优点

• 在二叉搜索树中搜索元素很容易，因为我们总能知道哪个子树包含所需元素。
• 与数组和链表相比，二叉搜索树中的插入和删除操作速度更快。

创建二叉搜索树的示例

现在，让我们通过一个例子来了解如何创建二叉搜索树。

假设数据元素是- 45, 15, 79, 90, 10, 55, 12, 20, 50

• 首先，我们将45插入树中作为根节点。
• 然后，读取下一个元素；如果它小于根节点，则将其插入为左子树的根，然后移动到下一个元素。
• 否则，如果元素大于根节点，则将其插入为右子树的根。

现在，让我们通过给定的数据元素来查看创建二叉搜索树的过程。创建BST的过程如下所示 -

步骤 1 - 插入 45。

步骤 2 - 插入 15。

由于15小于45，因此将其插入为左子树的根节点。

步骤 3 - 插入 79。

由于79大于45，因此将其插入为右子树的根节点。

步骤 4 - 插入 90。

90大于45和79，因此它将被插入为79的右子树。

步骤 5 - 插入 10。

10小于45和15，因此它将被插入为15的左子树。

步骤 6 - 插入 55。

55大于45且小于79，因此它将被插入为79的左子树。

步骤 7 - 插入 12。

12小于45和15，但大于10，因此它将被插入为10的右子树。

步骤 8 - 插入 20。

20小于45但大于15，因此它将被插入为15的右子树。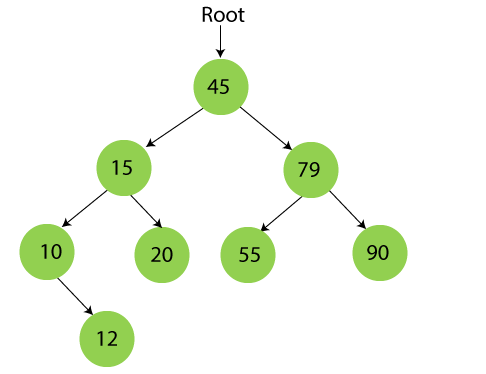

步骤 9 - 插入 50。

50大于45但小于79和55。因此，它将被插入为55的左子树。

现在，二叉搜索树的创建已完成。之后，让我们继续讨论可以在二叉搜索树上执行的操作。

我们可以在二叉搜索树上执行插入、删除和搜索操作。

让我们了解如何在二叉搜索树中执行搜索。

在二叉搜索树中搜索

搜索是指在数据结构中查找或定位特定元素或节点。在二叉搜索树中，搜索节点很容易，因为二叉搜索树中的元素是按特定顺序存储的。在二叉搜索树中搜索节点的步骤如下 -

1. 首先，将要搜索的元素与树的根元素进行比较。
2. 如果根与目标元素匹配，则返回节点的位置。
3. 如果不匹配，则检查该项是否小于根元素，如果小于根元素，则移动到左子树。
4. 如果大于根元素，则移动到右子树。
5. 递归地重复上述过程，直到找到匹配项。
6. 如果找不到元素或该元素不存在于树中，则返回 NULL。

现在，让我们通过一个例子来理解二叉树中的搜索。我们使用上面形成的二叉搜索树。假设我们要在下面的树中查找节点20。

步骤 1

步骤 2

步骤 3

现在，让我们看一下在二叉搜索树中搜索元素的算法。

在二叉搜索树中搜索元素的算法

现在，让我们了解如何在二叉搜索树中执行删除。我们还将通过一个例子来删除给定树中的一个元素。

在二叉搜索树中删除

在二叉搜索树中，我们必须在删除节点时牢记BST属性不被违反。要从BST中删除节点，有三种可能的情况 -

• 要删除的节点是叶节点，或者，
• 要删除的节点只有一个子节点，并且，
• 要删除的节点有两个子节点

我们将详细了解上面列出的情况。

当要删除的节点是叶节点时

这是BST中最简单的删除节点的情况。在这里，我们将叶节点替换为NULL，并简单地释放分配的内存。

我们可以从下面的图像中看到从BST删除叶节点的过程。在下面的图像中，假设我们要删除节点90。由于要删除的节点是叶节点，因此它将被替换为NULL，并且分配的内存将被释放。

当要删除的节点只有一个子节点时

在这种情况下，我们将目标节点替换为其子节点，然后删除子节点。这意味着在将目标节点替换为其子节点后，子节点将包含要删除的值。因此，我们只需将子节点替换为NULL并释放分配的内存。

我们可以在下面的图像中看到从BST删除只有一个子节点的节点的过​​程。在下面的图像中，假设我们要删除节点79。由于要删除的节点只有一个子节点，因此它将被其子节点55替换。

因此，替换后的节点79现在将成为叶节点，可以轻松删除。

当要删除的节点有两个子节点时

在BST中删除节点这种情况比其他两种情况要复杂一些。在这种情况下，要遵循的步骤如下 -

• 首先，找到要删除节点的后序（inorder）后继节点。
• 之后，将该节点替换为后序后继节点，直到目标节点位于树的叶子位置。
• 最后，将节点替换为NULL并释放分配的内存。

当右子节点不为空时，需要后序后继节点。我们可以通过找到节点右子树中的最小元素来获得后序后继。

我们可以从下面的图像中看到从BST删除有两个子节点的节点的过​​程。在下面的图像中，假设我们要删除根节点45。由于要删除的节点有两个子节点，因此它将被其后序后继节点替换。现在，节点45将位于树的叶子位置，以便可以轻松删除。

现在，让我们了解如何在二叉搜索树中执行插入。

在二叉搜索树中插入

BST中的新键始终在叶节点处插入。要将元素插入BST，我们必须从根节点开始搜索；如果要在插入的节点小于根节点，则在左子树中搜索空位置。否则，在右子树中搜索空位置并插入数据。BST中的插入类似于搜索，因为我们必须始终维护左子树小于根，右子树大于根的规则。

现在，让我们通过一个例子来了解将节点插入BST的过程。

二叉搜索树的复杂度

让我们看看二叉搜索树的时间和空间复杂度。我们将看到最佳情况、平均情况和最坏情况下的插入、删除和搜索操作的时间复杂度。

1. 时间复杂度

其中“n”是给定树中的节点数。

2. 空间复杂度

• 二叉搜索树所有操作的空间复杂度为 O(n)。

二叉搜索树的实现

现在，让我们看看实现二叉搜索树操作的程序。

程序：编写一个C++程序来实现二叉搜索树的操作。

在此程序中，我们将看到二叉搜索树操作的实现。在这里，我们将看到树的创建、中序遍历、插入和删除操作。

在这里，我们将看到树的中序遍历，以检查树的节点是否在其正确位置。我们知道中序遍历始终以升序给出数据。因此，在执行插入和删除操作后，我们进行中序遍历，遍历后，如果我们获得升序数据，那么就清楚节点在其正确位置。

输出

执行上述代码后，输出将是 -

所以，这就是关于本文的全部内容。希望本文能对您有所帮助并提供信息。