使用堆的时间复杂度

堆是一种特殊的基于树的数据结构，它符合堆属性。堆在编程和计算机科学应用中包括排序算法和优先级队列。主要有两种堆：

• 最大堆：最大堆是一组节点，其中每个节点 i 的值都大于或等于其所有子节点的值。这意味着最大元素位于堆的根部。优先级队列通常使用最大堆实现，其中优先级最高的元素始终位于最前面。
• 最小堆：在最小堆中，每个给定节点 i 的值都小于或等于其所有子节点的值。这意味着最小元素位于堆的根部。除其他用途外，优先级队列也可以与最小堆一起使用。

通常，堆被实现为二叉树。在 O(log n) 时间内，其中 'n' 是堆中元素的数量，二叉堆可以有效地处理插入、删除和确定最小或最大元素。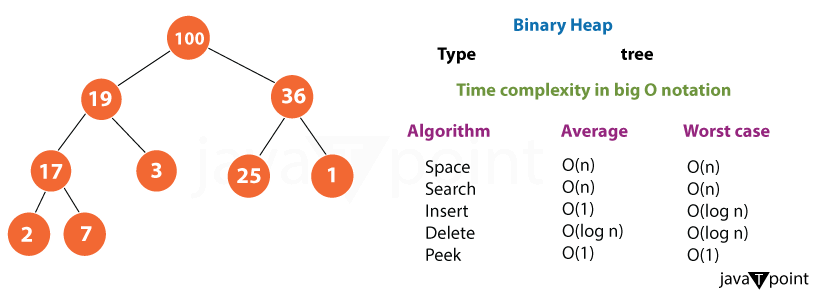

堆的常见用例包括：

• 优先级队列：优先级队列通常使用堆实现，其中优先级较高的项在优先级较低的元素之前出队。
• 堆排序：堆排序是一种基于比较的排序算法，它使用二叉堆将元素按升序或降序排列。
• Dijkstra 算法：为了确定加权图中的最短路径，Dijkstra 算法等图算法使用堆。
• 基于堆的数据结构：基于堆的二叉搜索树是可以使用堆作为基础构建的众多数据结构之一。
• 内存分配：为了有效地处理内存分配和释放，一些内存分配器使用堆数据结构。

使用堆的时间复杂度

根据所执行的特定操作，堆数据结构的时间复杂度各不相同。以下是典型的堆操作及其时间复杂度：

1. 插入（向上堆化）：在将新元素插入堆的过程中，它从底部开始“冒泡”或“向上渗透”通过树，直到恢复堆属性。此过程称为“向上堆化”。在大多数情况下，插入时间复杂度为 O(log n)，其中“n”是堆的元素计数。这是因为堆的高度与元素的数量呈对数关系。
2. 删除（向下堆化）：当删除根元素（例如最大堆中的最大元素或最小堆中的最小元素）时，堆中的最后一个元素将转移到根部，并通过树“向下冒泡”或“向下渗透”到其正确位置。删除的时间复杂度也是 O(log n)。
3. 查找最小值/最大值：因为最小值或最大值总是存储在堆的根部，所以确定最小堆中的最小元素或最大堆中的最大元素是一个 O(1) 操作。
4. 堆化（构建堆）：可以使用 O(n) 时间复杂度从组件数组创建堆。通常采用自下而上的策略来实现这一点，从叶子开始并逐渐“堆化”子树。
5. 堆排序：O(n log n) 排序算法“堆排序”基于重复提取表示最小（对于最小堆）或最大（对于最大堆）的元素并重建堆。
6. 更改键（更新键）：更改特定堆元素的值需要“向上堆化”或“向下堆化”操作，其时间复杂度为 O(log n)。

重要的是要记住，这些时间复杂度取决于堆结构保持平衡。如果堆变得不平衡，操作在时间方面可能会变得不那么复杂。此外，堆类型的选择可能会影响代码的实际性能，因为不同的堆类型（例如，二叉堆、斐波那契堆）对于特定操作可能具有略微不同的时间复杂度。

结论

总而言之，堆数据结构对于许多计算机科学和编程应用至关重要，因为它们提供了有效组织和处理具有特定特征数据的方法。最大堆和最小堆各自符合其堆特性，为插入、删除和识别极端元素等操作奠定了基础，所有这些都具有明确的时间复杂度。

在设计算法和为给定任务选择最佳数据结构时，理解堆操作所涉及的时间复杂性至关重要。尽管堆是有效的工具，但选择正确的堆变体（例如二叉堆或斐波那契堆）也可以提高代码的效率。

总而言之，堆在计算机科学和编程领域中是很有用的工具，因为它们是适应性强、有效的数据结构，具有广泛的用途。