访问数组位置以最大化分数

2025年2月7日 | 10分钟阅读

问题陈述

给定一个 0 索引的整数数组 nums 和一个正整数 x。我们最初在数组的位置 0，并且可以根据以下规则访问其他位置：

如果我们当前在位置 i，那么你可以移动到任何位置 j，其中 i < j。
对于你访问的每个位置 i，你将获得 nums[i] 的分数。
如果你从位置 i 移动到位置 j，并且 nums[i] 和 nums[j] 的奇偶校验不同，你将失去 x 分。

返回你能获得的最大总分数。

请注意，最初，你拥有 nums[0] 点。

示例 1

输入： nums = [2,3,6,1,9,2], x = 5

输出 13

说明

最初，你以 nums[0] = 2 的分数开始。
我们移动到位置 2（从 0 到 2），因为它是下一个有效位置。你的总分数变为 2 + nums[2] = 2 + 6 = 8。
现在，我们移动到位置 3（从 2 到 3）。这些位置的数字具有不同的奇偶校验（6 是偶数，1 是奇数），因此你将失去 x = 5 分。你的总分数变为 8 + nums[3] - x = 8 + 1 - 5 = 4。
最后，我们移动到位置 4（从 3 到 4）。你的总分数变为 4 + nums[4] = 4 + 9 = 13。
因此，通过遵循给定规则并选择要访问的最佳位置，你可以获得的最大总分数是 13。

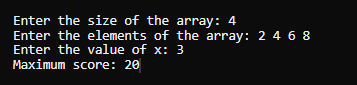
示例 2

输入： nums = [2,4,6,8], x = 3

输出 20

说明

最初，你以 nums[0] = 2 的分数开始。
我们移动到位置 1（从 0 到 1），因为它是下一个有效位置。你的总分数变为 2 + nums[1] = 2 + 4 = 6。
现在，我们移动到位置 2（从 1 到 2）。这些位置的数字具有相同的奇偶校验（4 是偶数，6 是偶数），因此你不会失去任何分数。你的总分数变为 6 + nums[2] = 6 + 6 = 12。
然后，我们移动到位置 3（从 2 到 3）。这些位置的数字具有相同的奇偶校验（6 是偶数，8 是偶数），因此你不会失去任何分数。你的总分数变为 12 + nums[3] = 12 + 8 = 20。
因此，通过遵循给定规则并选择要访问的最佳位置，你可以获得的最大总分数是 20。

示例 3

输入： nums = [3, 4, 1, 2, 8, 5], x = 3

输出 16

说明

最初，你以 nums[0] = 3 的分数开始。
我们移动到位置 1（从 0 到 1），因为它是下一个有效位置。你的总分数变为 3 + nums[1] = 3 + 4 = 7。
现在，我们移动到位置 2（从 1 到 2）。这些位置的数字具有不同的奇偶校验（4 是偶数，1 是奇数），因此你将失去 x = 3 分。你的总分数变为 7 - x = 7 - 3 = 4。
然后，我们移动到位置 3（从 2 到 3）。这些位置的数字具有相同的奇偶校验（1 是奇数，2 是偶数），因此你不会失去任何分数。你的总分数变为 4 + nums[3] = 4 + 2 = 6。
接下来，我们移动到位置 4（从 3 到 4）。这些位置的数字具有相同的奇偶校验（2 是偶数，8 是偶数），因此你不会失去任何分数。你的总分数变为 6 + nums[4] = 6 + 8 = 14。
最后，我们移动到位置 5（从 4 到 5）。这些位置的数字具有不同的奇偶校验（8 是偶数，5 是奇数），因此你将失去 x = 3 分。你的总分数变为 14 + nums[5] - x = 14 + 5 - 3 = 16。
因此，在这个例子中，你可以获得的最大总分数是 16。

Java 暴力解法

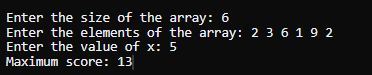
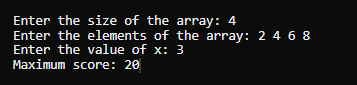import java. util.Scanner; 
public class Solution {
    public static void main(String[] args) {
Scanner scanner = new Scanner(System.in); 
System.out.println("Enter the size of the array:");
        int size = scanner.nextInt();
        int[] nums = new int[size]; 
        // Prompt the user to enter the elements of the array
System.out.println("Enter the elements of the array:");
        for (int i = 0; i < size; i++) {
nums[i] = scanner.nextInt();
        }
        // Prompt the user to enter the value of x
System.out.println("Enter the value of x:");
        int x = scanner.nextInt();
        // Create an instance of the Solution class
Solution solution = new Solution();
        // Calculate and print the maximum score
System.out.println("Maximum score: " + solution.maxScore(nums, x)); 
        // Close the scanner to prevent resource leak
scanner.close();
    }
    // Function to calculate the maximum score
    public long maxScore(int[] nums, int x) {
        // Initialize variables to store scores for starting with odd and even indices
        long startingWithOdd = 0l, startingWithEven = 0l; 
        // Adjust initial scores based on the parity of the first element
        if (nums[0] % 2 == 0) {
startingWithOdd = -x;
        }
        if (nums[0] % 2 != 0) {
startingWithEven = -x;
        }
        // Iterate through the array to update scores
        for (int n: nums) {
            // Update scores based on parity of current element
            if (n % 2 == 1) {
startingWithOdd = Math.max(startingWithOdd + n, startingWithEven + (n - x));
            } else {
startingWithEven = Math.max(startingWithEven + n, startingWithOdd + (n - x));
            }
        }
        // Return the maximum score among the two possibilities
        return Math.max(startingWithOdd, startingWithEven);
    }
}

输出

代码解释

初始化变量

初始化两个变量 startingWithOdd 和 startingWithEven，分别存储以奇数和偶数索引开始的分数。

调整初始分数

根据数组第一个元素 (nums[0]) 的奇偶校验来调整初始分数。
如果第一个元素是偶数，则将 startingWithOdd 设置为 -x。
如果第一个元素是奇数，则将 startingWithEven 设置为 -x。

遍历数组

遍历数组 nums 中的每个元素 n。

根据奇偶校验更新分数

根据当前元素 n 的奇偶校验更新分数。
如果 n 是奇数，则通过选择 (startingWithOdd + n) 和 (startingWithEven + (n - x)) 之间的最大值来更新 startingWithOdd。
如果 n 是偶数，则通过选择 (startingWithEven + n) 和 (startingWithOdd + (n - x)) 之间的最大值来更新 startingWithEven。

返回最大分数

返回两种可能性中的最大分数，即 Math.max(startingWithOdd, startingWithEven)。

时间复杂度

该算法的时间复杂度为 O(N)，其中 N 是输入数组中的元素数量。这是因为在算法识别最大分数时，数组中的每个元素都会被遍历一次。

空间复杂度

空间复杂度为 O(1)，因为算法使用的额外空间是恒定的，取决于输入的大小。只需要另外两个变量来存储分数。数组在原地修改，不使用任何额外的数据结构。因此，空间复杂度将是常数。

Java 动态规划方法

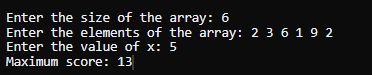
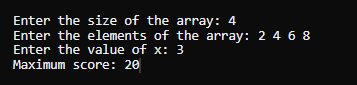import java. util.Arrays;
import java. util.Scanner; 
public class Solution {
    // Function to calculate the maximum total score for the subsequence
    public long maxTotalScore(int[] nums, int x, int i, int lastParity, long[][] dp) {
        // Base case: If we reach the end of the array, return 0
        if (i + 1 == nums.length) {
            return 0;
        }
        // If the result is already computed, return it
        if (dp[i][lastParity] != -1) return dp[i][lastParity]; 
        // Recursive cases
        long notPick = maxTotalScore(nums, x, i + 1, lastParity, dp);
        long pick = Integer.MIN_VALUE;
        if (lastParity == nums[i + 1] % 2) {
pick = nums[i + 1] + maxTotalScore(nums, x, i + 1, lastParity, dp);
        } else {
pick = maxTotalScore(nums, x, i + 1, nums[i + 1] % 2, dp) - x + nums[i + 1];
        }
        // Store the result in the dp table and return
        return dp[i][lastParity] = Math.max(pick, notPick);
    }
    // Function to calculate the maximum score
    public long maxScore(int[] nums, int x) {
        // Initialize the dp table with -1
long[][] dp = new long[nums.length][2];
        for (int i = 0; i < dp.length; i++) {
Arrays.fill(dp[i], -1);
        }
        // Calculate the maximum total score for the subsequence
        return nums[0] + maxTotalScore(nums, x, 0, nums[0] % 2, dp);
    }
    public static void main(String[] args) {
Scanner scanner = new Scanner(System.in); 
System.out.println("Enter the size of the array:");
        int size = scanner.nextInt();
        int[] nums = new int[size]; 
        // Prompt the user to enter the elements of the array
System.out.println("Enter the elements of the array:");
        for (int i = 0; i < size; i++) {
nums[i] = scanner.nextInt();
        }
        // Prompt the user to enter the value of x
System.out.println("Enter the value of x:");
        int x = scanner.nextInt();
        // Create an instance of the Solution class
Solution solution = new Solution();
        // Calculate and print the maximum score
System.out.println("Maximum score: " + solution.maxScore(nums, x)); 
        // Close the scanner to prevent resource leak
scanner.close();
    }
}

输出

代码解释

计算最大分数函数 (maxScore)

初始化 DP 表

初始化一个维度为 (nums.length) x (2) 的二维数组 dp 来存储计算结果。
将 dp 的所有元素初始化为 -1，表示结果尚未计算。

计算子序列的最大总分数 (maxTotalScore)

调用 maxTotalScore 方法，参数为：nums、x、0（初始索引）、nums[0] % 2（第一个元素的奇偶校验）和 dp。
maxTotalScore 是一个递归函数，用于计算子序列的最大总分数。

计算子序列的最大总分数函数 (maxTotalScore)

基本情况

如果索引 i 到达数组末尾，则返回 0。

记忆化

如果当前状态的结果已计算，则从记忆化数组 (dp) 中返回它。

递归情况

计算不选择当前元素（notPick）时的最大总分数。
计算选择当前元素（pick）时的最大总分数，同时考虑奇偶校验约束和 x 的值。
在选择和不选择当前元素之间选择最大分数。

将结果存储在 DP 表中

将结果记忆化存储在记忆化数组 (dp) 中。
返回最大分数。

输出最大分数

打印最大分数
打印计算出的最大分数。

时间复杂度

所提出的解决方案的时间复杂度为 O(N)，其中 N 是数组的大小。这种情况之所以可能，是因为该解决方案结合了动态规划和记忆化，其中每个子问题至少被解决一次。

空间复杂度

此方法的空间复杂度也为 O(N)，N 为输入数组的元素数量。这是因为实现了一个二维记忆化表来保存子问题的结果，该表需要大致与输入数组成比例的空间。此外，其余的辅助变量都是常数空间复杂度，这意味着它们不会对整体空间复杂度产生显著影响。

Java 记忆化方法

im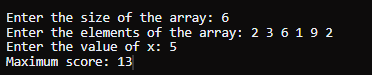port java. util.Arrays;
import java. util.Scanner; 
public class Solution {
    static int n;
    static long dp[][];
    public static void main(String[] args) {
Scanner scanner = new Scanner(System.in); 
System.out.println("Enter the size of the array:");
        int size = scanner.nextInt();
        int[] nums = new int[size]; 
        // Prompt the user to enter the elements of the array
System.out.println("Enter the elements of the array:");
        for (int i = 0; i < size; i++) {
nums[i] = scanner.nextInt();
        }
        // Prompt the user to enter the value of x
System.out.println("Enter the value of x:");
        int x = scanner.nextInt();
        // Create an instance of the Solution class
Solution solution = new Solution();
        // Calculate and print the maximum score
System.out.println("Maximum score: " + solution.maxScore(nums, x)); 
        // Close the scanner to prevent resource leak
scanner.close();    
    // Function to find the maximum score
    public long maxScore(int[] arr, int x) {
        n = arr. length;
        dp = new long[n + 1][2]; 
        // Base case: Initialize the last row of dp with 0
        for (int i = n - 1; i >= 0; i--) {
for (int flag = 0; flag <= 1; flag++) {  
int check = arr[i] % 2;   
long take = 0;   
if (check == flag) {                   
take = arr[i] + dp[i + 1][check];               
} else {                   
take = (arr[i] - x) + dp[i + 1][check];  
}  
long nt = dp[i + 1][flag]; 
// Update dp[i][flag] with the maximum of nt and take    
dp[i][flag] = Math.max(nt, take); }
        }
        // Return the maximum score
        return dp[0][arr[0] % 2];
    }
    // Function to solve recursively (not used in final solution)
    long solve(int i, int flag, int arr[], int x) {
        if (i == n) return 0; 
        if (dp[i][flag] != -1) return dp[i][flag]; 
        int check = arr[i] % 2;
        long take = 0;
        if (check == flag) {
take = arr[i] + solve(i + 1, check, arr, x);
        } else {
take = (arr[i] - x) + solve(i + 1, check, arr, x);
        }
        long nt = solve(i + 1, flag, arr, x); 
        return dp[i][flag] = Math.max(nt, take);
    }
}

输出

代码解释

初始化

初始化一个大小为 (n + 1) x 2 的二维 DP 数组 dp[][]，其中 n 是数组 nums 的长度。
将 dp 的最后一行初始化为零，因为它表示从最后一个元素开始可获得的最大分数。

自底向上 DP 方法

从右到左遍历数组 nums。
在每个索引 i 处，遍历奇偶校验（偶数和奇数）。
对于每种奇偶校验，计算可以通过包含当前元素或跳过当前元素来获得的最大分数。
- 如果当前元素的奇偶校验与前一个元素的奇偶校验匹配
- 通过将当前元素的值添加到迄今为止获得的分数 (dp[i + 1][parity]) 来计算分数。
- 如果当前元素的奇偶校验与前一个元素的奇偶校验不匹配
- 通过将当前元素的值减去 x，然后将其添加到来自下一个具有相反奇偶校验的元素的分数 (dp[i + 1][opposite_parity]) 来计算分数。
使用两个选项中获得的最大分数更新 dp[i][parity]。

返回最大分数

可获得的最大分数将存储在 dp[0][parity] 中，其中 parity 是数组第一个元素的奇偶校验。

输出

打印获得的最大分数。

时间复杂度

该解决方案的时间复杂度为 O(n)，其中 n 是包含要排序的数字的数组的大小。这是因为该算法遍历了数组的每个元素，并在一次迭代中计算了最大元素。每次迭代只需要恒定时间的操作。

空间复杂度

该算法的空间复杂度为 O(n)，这是线性的，因为 n 是输入数组的大小值。由于使用了大小为 (n + 1) * 2 的二维数组 'dp' 来计算每个元素及其石头的奇偶校验的分数，因此该实现可能看起来难以理解。此外，由于 dp 数组与它的重要性相比甚至更小，因此实现的其他常量并不多。

下一主题什么是对数时间复杂度

访问数组位置以最大化分数

问题陈述

示例 1

示例 2

示例 3

Java 暴力解法

代码解释

Java 动态规划方法

代码解释

Java 记忆化方法

代码解释

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

访问数组位置以最大化分数

问题陈述

示例 1

示例 2

示例 3

Java 暴力解法

代码解释

Java 动态规划方法

代码解释

Java 记忆化方法

代码解释

相关帖子

严格二叉树

2-3 树 (搜索、插入和删除)

二叉树的性质

压缩线段树并在 O(N*logN) 中合并集合

检查二维矩阵中是否存在可能的路径

第 k1 小和第 k2 小元素之间的所有元素之和

什么是 K 连通图

螺旋形式打印给定矩阵

何时应使用 List vs LinkedList

Python 中数组轮换的块交换算法

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器