数据结构中的栈2025年4月21日 | 阅读 10 分钟 栈是一种线性数据结构,遵循 后进先出 (LIFO) 原则。栈只有一个端点,而队列有两个端点(前端和后端)。它只有一个指针 栈顶指针,指向栈顶元素。每当一个元素被添加到栈中时,它都会被添加到栈顶,并且只能从栈顶删除元素。换句话说,栈可以定义为一个容器,其中插入和删除只能从一个称为栈顶的端点进行。 与栈相关的一些要点- 它被称为栈,因为它像现实生活中的栈一样工作,例如书本堆叠等。
- 栈是一种抽象数据类型,具有预定义的容量,这意味着它可以存储有限大小的元素。
- 它是一种数据结构,它遵循一定的顺序来插入和删除元素,该顺序可以是 LIFO 或 FILO。
- 栈中的元素遵循垂直线性排列
- 可视化一个物理对象堆栈有助于理解概念
- 虽然具有定义的容量,但堆栈大小限制是灵活的
- 栈的应用超出了基本数据结构的范畴
- 适用于算法设计、语言处理、时间顺序
- 非常适合回溯、表达式转换、嵌套操作
- 系统化的排序有助于模拟现实世界的顺序场景
栈的工作原理栈遵循 LIFO 模式。正如我们在下面的图中观察到的,栈中有五个内存块;因此,栈的大小是 5。 假设我们要将元素存储在栈中,并且假设栈是空的。我们已经创建了一个大小为 5 的栈,如下所示,我们将一个接一个地压入元素,直到栈满。 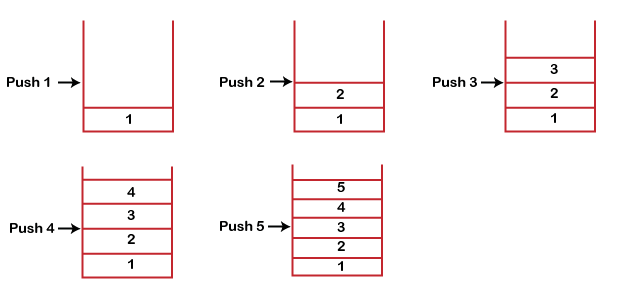 由于我们的栈已满(栈大小为 5)。在上面的情况中,我们可以观察到,当我们向栈中输入新元素时,它是从顶部到底部的。栈是从底部到顶部填充的。 当我们对栈执行删除操作时,只有一个输入和输出的方式,因为另一端是封闭的。它遵循 LIFO 模式,这意味着先输入的值将最后被删除。在上面的情况下,值 5 是第一个输入的,因此只有在删除所有其他元素后才能删除它。 - 栈严格遵守后进先出 (LIFO) 原则来进行元素的插入和删除。
- 设想一个垂直堆栈,顶部是用于添加和删除的活动端。
- 最初,当创建一个栈时,它被标记为空,栈顶指针设置为一个哨兵值,例如 -1。
- 在插入(push 操作)期间,元素被放置在当前栈顶位置,然后栈顶指针递增。
- 此 push 过程将继续,直到达到栈的预定容量,之后将无法进行插入。
- 对于删除(pop 操作),会检索并返回当前栈顶的元素。
- 同时,栈顶指针递减,从而从栈中移除该顶部元素。
- 尝试在空栈上执行 pop 操作会触发下溢条件,表明这是一个错误的操作。
- 栈在 push 时向上增长,在 pop 时向下收缩,保持 LIFO 顺序。
- 这种在单个端点上进行的有组织的添加和删除是栈在其所有操作中的基本属性。
栈的算法- 可以使用数组或链表数据结构来实现栈
- 对于数组实现,我们需要在初始时为栈定义一个固定大小
- 我们维护一个“top”变量,它跟踪栈中顶部元素的位置索引
- 最初,“top”设置为 -1,表示栈为空
- 可以在栈上执行以下操作
- 推送操作
- 检查栈是否已满 (top == size - 1)
- 如果已满,则返回错误(栈溢出)
- 如果未满,则递增“top”,并将新元素插入到新的“top”索引处
- Pop(出栈)操作
- 检查栈是否为空 (top == -1)
- 如果为空,则返回错误(栈下溢)
- 如果不为空,则检索“top”索引处的元素
- 将“top”递减 1,以移除顶部元素
- Peek 操作
- 检查栈是否为空 (top == -1)
- 如果为空,则返回错误
- 如果不为空,则返回“top”索引处的元素(而不移除它)
- isEmpty 操作
- 检查“top”是否等于 -1
- 如果是,则返回 true(栈为空)
- 如果否,则返回 false(栈不为空)
- isFull 操作
- 检查“top”是否等于 size - 1
- 如果是,则返回 true(栈已满)
- 如果否,则返回 false(栈未满)
栈实现算法初始化一个大小为“n”的数组“stack” 初始化“top”为 -1 此算法概述了使用数组数据结构实现栈数据结构的基本操作及其实现。push、pop 和 peek 操作的时间复杂度为 O(1),因为它们涉及常数时间操作。但是,空间复杂度为 O(n),其中“n”是用于实现栈的数组的固定大小。 标准栈操作以下是一些在栈上实现的常见操作 - Push (item): 将新元素“item”插入到栈顶。但是,如果栈已达到最大容量,则尝试 push 会导致溢出错误条件。
- pop(): 从栈中移除并返回顶部元素。但是,如果栈为空,尝试 pop 会触发下溢错误,因为没有元素可以移除。
- peek(): 检索栈顶元素的值而不将其从栈中移除。如果栈为空,则表示错误状态。
- isEmpty(): 通过检查栈顶指针是否指向哨兵值(例如 -1)来检查栈是否为空。如果栈为空,则返回 true;否则返回 false。
- isFull(): 通过检查栈顶指针是否位于最后一个有效索引上来确定栈是否已达到最大容量。如果已满,则返回 true;否则返回 false。
- size(): 返回当前栈中元素的数量。
- top(): 类似于 peek(),访问并返回栈顶元素的值而不将其移除。peek() 的别名。
- display(): 输出栈中的所有元素,通常是从顶部到底部遍历。
此外,一些高级操作包括 - clear(): 移除栈中的所有元素,将其重置为空状态。
- reverse(): 反转栈中元素的顺序。
- contains(item): 检查给定的“item”是否存在于栈中,返回 true 或 false。
这些操作涵盖了有效操作和处理栈数据结构的基本功能。具体的实现细节可能因底层数据结构(例如数组或链表)和编程语言而异。 PUSH 操作PUSH 操作涉及的步骤如下 - 在栈中插入元素之前,我们会检查栈是否已满。
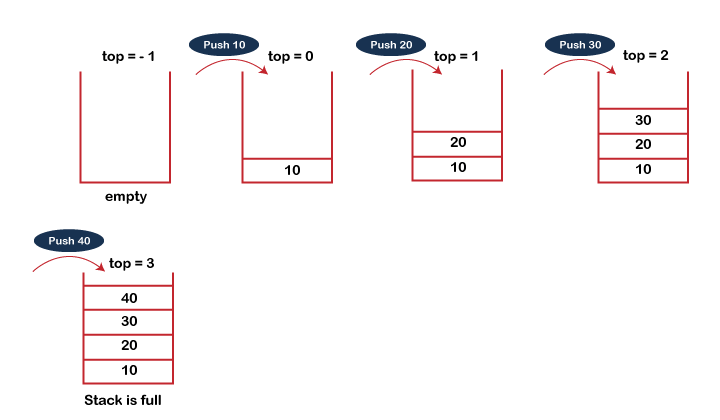
- 如果我们尝试将元素插入栈中,而栈已满,则会发生 溢出 条件。
- 当我们初始化一个栈时,我们将 top 的值设置为 -1,以检查栈是否为空。
- 当新元素被推入栈时,首先,top 的值会递增,即 top=top+1,元素将被放置在 top 的新位置。
- 元素将被插入,直到我们达到栈的 最大 大小。
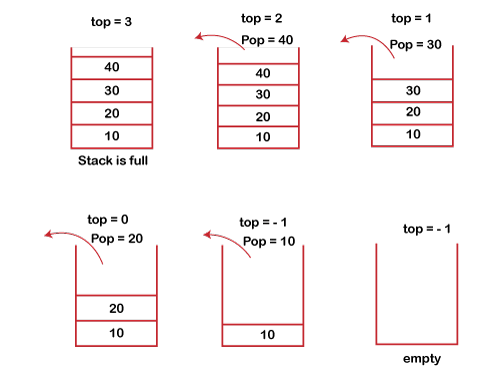
 POP 操作POP 操作涉及的步骤如下 - 在从栈中删除元素之前,我们会检查栈是否为空。
- 如果我们尝试从空栈中删除元素,则会发生 下溢 条件。
- 如果栈不为空,我们首先访问由 top 指向的元素
- 执行 pop 操作后,top 会减 1,即 top=top-1。
 栈的实现C 语言程序 输出  Python 程序 输出  在 C 程序中,我们使用数组来实现栈,最大固定大小为 100。我们定义了 push、pop、peek、isEmpty 和 isFull 操作函数。 在 Python 程序中,我们创建了一个 Stack 类,其中包含 push、pop、peek、isEmpty 和 size 操作的方法。我们使用 Python 列表作为底层数据结构来存储栈元素。 这两个程序都演示了栈数据结构的基本操作,包括将元素压入栈、从栈顶弹出元素、查看栈顶元素、检查栈是否为空或已满以及获取栈的大小。 您可以随意尝试这些程序,根据需要修改它们,或扩展其功能以满足您的要求。 栈的应用以下是栈的应用 众所周知,每个程序都有开括号和闭括号。当出现开括号时,我们将括号压入栈中;当出现闭括号时,我们从栈中弹出开括号。因此,净值最终为零。如果栈中还有任何符号,则表示程序中存在语法错误。 使用栈的优点;- 维护顺序:栈自然地跟踪元素的添加和删除顺序,遵循后进先出 (LIFO) 原则。此功能对于需要处理或回溯的任务很有用。
- 高效的操作:push、pop 和 peek 等关键栈操作的时间复杂度为 O(1),可确保元素的插入和删除。
- 内存管理支持:栈在递归期间在管理函数调用栈方面发挥作用,有助于为变量分配和释放内存。
- 反转功能:栈可以通过按推入的顺序弹出元素来反转字符串、表达式或序列。
- 表达式转换辅助:栈对于将表达式从中缀、前缀和后缀表示法之间进行转换至关重要。这是编译器和表达式求值器的功能。
- 撤销/重做功能:栈的后进先出特性使其非常适合在文本编辑器、图形工具或交互式应用程序中实现撤销/重做功能。
与栈相关的缺点- 大小限制:在基于数组的实现中,栈的大小在初始化时是固定的;如果低估大小,可能会导致栈溢出。
- 访问范围有限:栈中的元素只能从顶部访问,这使得搜索或访问位于栈底部区域的元素效率低下。
- 单向操作:栈允许从一个端点(顶部)添加和删除元素,这限制了与队列或双向链表等数据结构相比的通用性。
- 额外的内存使用:在使用链表时,每个节点都需要内存来保存指针,这可能导致空间效率低下,尤其是对于大型栈。
| 



