树 (数据结构)

引言

我们学习了线性数据结构，如数组、链表、栈和队列，其中所有元素都按顺序排列。有些数据组织需要将数据分类到组和子组中。不同的数据结构用于不同的数据类型。

选择数据结构时会考虑一些因素

• 需要存储什么类型的数据？：某些数据结构可能最适合某种类型的数据。
• 操作成本：如果我们希望尽量降低最常执行的操作的成本。例如，我们有一个简单的列表，我们需要对其执行搜索操作；然后，我们可以创建一个按排序顺序存储元素的数组，以执行二分查找。二分查找对简单列表非常快，因为它将搜索空间一分为二。
• 内存使用：有时，我们想要一种内存占用较少的数据结构。

什么是树数据结构？

树是由有限个节点组成的集合，其中有一个特殊的节点称为根节点，其余节点可以被分成零个、一个或多个不相交的子集，每个子集本身也是一棵树，称为T的子树。

假设我们想以层级形式显示员工及其职位，则可以如下所示表示：

上图显示了一家公司某部门的组织层级。在上述结构中，john是公司的CEO，John有两名直接下属，名为Steve和Rohan。Steve有三名直接下属，名为Lee, Bob, Ella，其中Steve是经理。Bob有两名直接下属，名为Sal和Emma。Emma有两名直接下属，名为Tom和Raj。Tom有一名直接下属，名为Bill。这种特定的逻辑结构称为树。其结构与真实树相似，因此称为树。在此结构中，根位于顶部，其分支向下延伸。因此，我们可以说树数据结构是一种以层级方式存储数据的有效方法。

让我们来了解树数据结构的一些关键点。

• 树数据结构被定义为由节点组成的对象或实体的集合，这些节点相互链接以表示或模拟层级结构。
• 树数据结构是非线性数据结构，因为它不按顺序存储。它是一种层级结构，因为树中的元素分布在多个级别。
• 在树数据结构中，最顶端的节点称为根节点。每个节点都包含一些数据，数据可以是任何类型。在上面的树结构中，节点包含员工姓名，因此数据类型将是字符串。
• 每个节点都包含一些数据以及指向其他子节点的链接或引用，这些子节点可以称为子节点。
• 在树数据结构中，节点不包含任何循环。

树数据结构中使用的一些基本术语。

让我们考虑下面显示的树结构

在上述结构中，每个节点都用字母标记。图中的每条箭头都称为两个节点之间的链接。

• 根节点：根节点是树层级结构中最顶端的节点。换句话说，根节点是没有任何父节点的节点。在上述结构中，编号为 A 的节点是树的根节点。如果一个节点直接链接到另一个节点，则称为父子关系。
• 节点：树中存储数据元素的节点，可能有一个或多个指向其他子孙节点的链接用于连接。它可以是父节点、子节点，或两者兼有。

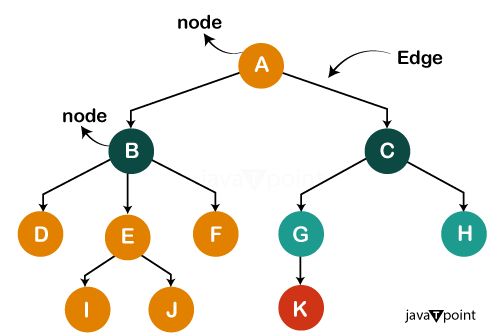在上面的例子中，A、B、C 等都是树的节点。

• 边：任意两个节点之间的链接称为边。从一个节点到另一个后继节点的有向线称为树的边。具有 'N' 个顶点的树最多可以有 'N-1' 条边。

在上面的图示表示中，我们看到了节点之间的各种边。例如：顶点 A 和顶点 C 之间的边，顶点 B 和顶点 D 之间的边等等。

• 子节点：如果一个节点是任何节点的后代，那么该节点就称为子节点。父节点可以有任意数量的子节点。树中的每个节点都可以有零个或多个子节点。

在上面的例子中，任何节点的后代都显示了子节点。例如：节点 G、节点 K 是节点 D 的子节点，也是节点 B 的子节点。G 和 H 是节点 C 的左子节点和右子节点。

• 父节点：父节点也可以称为“拥有子节点的节点”。如果一个节点包含任何子节点，那么该节点就是该子节点的父节点。

在上面的例子中，任何节点的祖先都显示为父节点。例如：节点 A、节点 B 和节点 G 等都是父节点。

• 兄弟节点：拥有相同父节点的节点称为兄弟节点。

在上面的例子中，显示了拥有相同父节点的节点称为兄弟节点。例如：节点 G 和节点 H 是兄弟节点。

• 叶节点：树中没有子节点的节点称为叶节点。叶节点是树中最底端的节点。在普通树中可以存在任意数量的叶节点。叶节点也称为外部节点和终端节点。

在上面的例子中，显示了各种叶节点，如节点 D、F、K 等。

• 内部节点：至少有一个子节点的节点称为内部节点，也是树数据结构中的非终端节点。

在上面的例子中，显示了各种内部节点，如节点 A、B、C、G 等。

• 祖先节点：节点的祖先是从根节点到该节点路径上的任何祖先节点。根节点没有祖先。在上面图像所示的树中，节点 1、2 和 5 是节点 10 的祖先。
• 后代：给定节点的直接后继称为节点的后代。在上图中，10 是节点 5 的后代。
• 度：节点子节点的总数称为该节点在树数据结构中的度。

在上面的图示表示中，我们看到了从起点到终点的各种节点的度。例如：节点 K 的度为 0，节点 E 的度为 1 等。

• 子树：如果一棵树被进一步划分为更小的树，则称为树数据结构中的子树。子树是树的一部分，可以看作是一棵完整的树，其中每个子节点都形成其父节点的子树。下面的例子显示了不同的子树。

• 层级：节点的层级是一个整数值，用于测量节点到根节点的距离。例如：根节点位于层级 0，根节点的子节点位于其下一层（层级 1），依此类推。

上述图示表示显示了从根节点（即层级 0）开始的层级 3。

• 路径：路径是从源节点到另一个节点（即目标节点）的连续边和节点的序列。

在上面的例子中，从节点 A 到节点 J 的路径是“A - B - E - J”，路径长度为 4。

树数据结构的属性

• 递归数据结构：树也称为递归数据结构。树可以递归定义，因为树数据结构中的一个特殊节点称为根节点。树的根节点包含指向其所有子树根节点的链接。左子树在下图的黄色区域中显示，右子树在红色区域中显示。左子树可以进一步划分为显示为三种不同颜色的子树。递归意味着以自相似的方式减少事物。因此，树数据结构的这种递归属性在各种应用中都有实现。
  
• 边数：如果有 n 个节点，则有 n-1 条边。结构中的每条箭头都代表链接或路径。除根节点外的每个节点都至少有一个指向子节点的入向链接，称为边。父子关系将有一条链接。
• 节点 x 的深度：节点 x 的深度可以定义为从根节点到节点 x 的路径长度。一条边贡献路径的一个单位长度。因此，节点 x 的深度也可以定义为根节点和节点 x 之间的边数。根节点的深度为 0。
  
• 节点 x 的高度：节点 x 的高度可以定义为从节点 x 到叶节点的 longest path（最长路径）。
  

根据树数据结构的属性，树分为各种类别。

树的实现

可以通过使用指针动态创建节点来创建树数据结构。内存中的树表示如下所示：

上图显示了内存中树数据结构的表示。在上图中，节点包含三个字段。第二个字段存储数据；第一个字段存储左子节点的地址，第三个字段存储右子节点的地址。

在编程中，节点的结构可以定义为

上述结构只能为二叉树定义，因为二叉树最多可以有两个子节点，而通用树可以有多个子节点。通用树的节点结构将与二叉树不同。

树的应用

以下是树的应用

• 存储自然层级数据：树用于以层级结构存储数据。例如，文件系统。存储在磁盘驱动器上的文件系统、文件和文件夹是以自然层级数据形式存储并以树的形式存储的。
• 组织数据：它用于组织数据以进行高效的插入、删除和搜索。例如，二叉树的搜索元素时间复杂度为 logN。
• Trie：它是一种特殊的树，用于存储字典。它是动态拼写检查的快速有效的方法。
• 堆：它也是一种使用数组实现的树数据结构。它用于实现优先队列。
• B 树和 B+ 树：B 树和 B+ 树是用于在数据库中实现索引的树数据结构。
• 路由表：树数据结构也用于在路由器中存储路由表数据。
• 解析树：树数据结构可用于创建解析树来评估算术表达式。

树数据结构类型

以下是树数据结构的类型

• 普通树：普通树是树数据结构的一种类型。在普通树中，一个节点可以有 0 个或最多 n 个节点。对节点的度（节点可以包含的节点数）没有限制。普通树中最顶端的节点称为根节点。父节点的子节点称为子树。
  
  普通树中可以有n个子树。在普通树中，子树是无序的，因为子树中的节点不能排序。
  每个非空树都有向下的边，这些边连接到称为子节点的节点。根节点标记为层级 0。拥有相同父节点的节点称为兄弟节点。
• 二叉树：这里，二叉名称本身就表示两个数字，即 0 和 1。在二叉树中，树中的每个节点最多可以有两个子节点。这里，最多表示节点有 0 个、1 个或 2 个子节点。
  
  要了解更多关于二叉树的信息，请点击下面的链接
  binary-tree
• 二叉搜索树：二叉搜索树是一种非线性数据结构，其中一个节点连接到n个节点。它是一种基于节点的结构。节点可以用三个字段表示，即数据部分、左子节点和右子节点。在二叉搜索树中，一个节点最多可以连接到两个子节点，因此节点包含两个指针（左子节点和右子节点指针）。
  左子树中的每个节点都必须包含小于根节点的值，而右子树中的每个节点的值都必须大于根节点的值。

节点可以通过称为struct的用户定义数据类型创建，如下所示

以上是带有三个字段的节点结构：数据字段，第二个字段是节点类型的左指针，第三个字段是节点类型的右指针。

要了解更多关于二叉搜索树的信息，请点击下面的链接

binary-search-tree

• AVL 树

它是二叉树的一种，或者我们可以说它是二叉搜索树的一个变体。AVL 树同时满足二叉树和二叉搜索树的属性。它是一种自平衡二叉搜索树，由Adelson Velsky Lindas发明。这里的自平衡意味着平衡左子树和右子树的高度。这种平衡通过平衡因子来衡量。

如果我们考虑一棵树是 AVL 树，那么这棵树就遵循二叉搜索树以及平衡因子。平衡因子可以定义为左子树高度与右子树高度之差。平衡因子的值必须是 0、-1 或 1；因此，AVL 树中的每个节点的平衡因子值都必须是 0、-1 或 1。

要了解更多关于 AVL 树的信息，请点击下面的链接

avl-tree

• 红黑树

红黑树是二叉搜索树。红黑树的前提是我们应该了解二叉搜索树。在二叉搜索树中，左子树的节点值应该小于该节点的值，而右子树的节点值应该大于该节点的值。正如我们所知，二分查找在平均情况下的时间复杂度是 log₂n，最佳情况是 O(1)，最坏情况是 O(n)。

当在树上执行任何操作时，我们希望我们的树是平衡的，以便所有操作如搜索、插入、删除等都能花费更少的时间，并且所有这些操作的时间复杂度都将是log₂n。

红黑树是一种自平衡二叉搜索树。AVL 树也是一种高度平衡的二叉搜索树，那么为什么我们需要红黑树？在 AVL 树中，我们不知道需要多少次旋转才能平衡树，但在红黑树中，最多需要 2 次旋转才能平衡树。它包含一个额外的位，用于表示节点的红色或黑色，以确保树的平衡。

• 伸展树

伸展树数据结构也是一种二叉搜索树，其中最近访问的元素通过执行一些旋转操作被放置在树的根节点位置。这里的伸展意味着最近访问的节点。它是一种自平衡二叉搜索树，没有像AVL树那样的显式平衡条件。

伸展树的高度可能不平衡，即左右子树的高度可能不同，但伸展树中的操作花费的时间复杂度是logN，其中n是节点数。

伸展树是一种平衡树，但它不能被认为是高度平衡树，因为每次操作后都会执行旋转，从而导致一棵平衡树。

• Treap

Treap 数据结构来自树和堆数据结构。因此，它包含了树和堆数据结构的属性。在二叉搜索树中，左子树的每个节点必须等于或小于根节点的值，右子树的每个节点必须等于或大于根节点的值。在堆数据结构中，左右子树都包含大于根节点的键；因此，我们可以说根节点包含最小值。

在 treap 数据结构中，每个节点都有键和优先级，其中键来自二叉搜索树，优先级来自堆数据结构。

Treap 数据结构遵循两个属性，如下所示：

• 节点的右子节点 >= 当前节点，节点的左子节点 <= 当前节点（二叉树）
• 任何子树的子节点必须大于节点（堆）

• B 树

B 树是一种平衡的m 路树，其中m定义了树的阶数。到目前为止，我们了解到节点只包含一个键，但 b 树可以包含多个键和多个子节点。它始终维护排序数据。在二叉树中，叶节点可能位于不同的层级，但在 b 树中，所有叶节点必须位于同一层级。

如果阶数为 m，则节点具有以下属性：

• B 树中的每个节点最多可以有 m 个子节点
• 对于最少子节点，叶节点有 0 个子节点，根节点最少有 2 个子节点，内部节点最少有 m/2 的向上取整个子节点。例如，m 的值为 5，表示一个节点最多可以有 5 个子节点，内部节点最多可以包含 3 个子节点。
• 每个节点最多包含 (m-1) 个键。

根节点必须包含最少 1 个键，所有其他节点至少必须包含向上取整的 m/2 减 1 个键。

关于树数据结构的填空题

1. 下列哪项是非线性数据结构？

1. Stack
2. Tree
3. 字符串
4. 列表

2. AVL 树是一种二叉搜索树，其中每个节点都有一个平衡因子？

1. 平衡因子 0
2. 平衡因子 1
3. 平衡因子 -1
4. 平衡因子 1, 0, -1

3. 二叉树的前序遍历是 a, B, D, E, H, I, C, F。该树的顺序遍历是？

1. D, B, G, E, H, I, A, C, F
2. D, B, G, H, E, I, A, C, F
3. D, F, G, H, E, I, A, C, B
4. A, B, G, H, E, I, D, C, F

4. 高度为 h 的二叉树可能拥有的最少节点数是多少？

1. h - 2
2. h + 2
3. h - 1
4. h + 1

5. 在 B 树中，每个节点最多可以有多少个子节点（键值对）？

1. m-1
2. m + 2
3. m - 2
4. m + 1

6. 堆树是一种完全二叉树，其中任何节点存储的数据值？

1. 等于子节点的值
2. 大于子节点
3. 小于子节点
4. 大于或等于子节点的值