条件概率的贝叶斯公式

贝叶斯定理指出，一个事件的概率是基于与该事件相关的条件的先验知识。它也用于检验条件概率的情况。如果我们知道条件概率，我们可以使用贝叶斯公式计算逆概率。让我们通过一个例子来理解这个概念。假设我们必须从三个不同的球袋中取出第二个袋子中的黑球的概率，其中每个袋子包含三种不同的球，如红色、蓝色、黑色。在这种情况下，事件发生的概率取决于其他条件，这被称为条件概率。在本文中，我们将讨论贝叶斯定理的陈述和证明、公式、推导以及示例。

在事件 B 发生的情况下事件 A 发生的概率等于事件 A 发生的概率与在事件 A 发生的情况下事件 B 发生的概率的乘积，再除以事件 B 发生的概率。

如果你抛掷两枚硬币，它们都出现反面的概率是多少？有四种可能的结果；

硬币 1：正面，硬币 2：正面

硬币 1：正面，硬币 2：反面

硬币 1：反面，硬币 2：正面

硬币 1：反面，硬币 2：反面

这些结果中只有一个是“都出现反面”的情况。因此，我们有四分之一的机会得到两个反面，这是简单概率的基本示例。

“条件”部分体现在我们开始加入额外信息。现在，我们提出一个问题：“如果硬币 1 出现正面，那么我们得到两个正面的概率是多少？”

硬币 1：正面，硬币 2：正面

硬币 1：正面，硬币 2：反面

因此，在硬币 1 出现正面的条件下，得到两个正面的概率是二分之一。

贝叶斯定理的陈述

设 E₁, E₂, E₃,…….En 是与样本空间 S 相关的一组事件，其中所有事件 E₁, E₂, E₃,…….En 都有非零的发生概率，并且它们构成 S 的一个划分。设 A 是与样本空间 S 相关的事件，那么根据贝叶斯定理。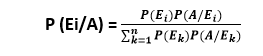

对于变量 k = 1,2, 3,…..n

贝叶斯定理的证明

根据条件概率公式

基于贝叶斯定理的例子

示例 1

袋子 P 装有 6 个白球和 6 个蓝球，而另一个袋子 Q 装有 3 个白球和 3 个蓝球。随机从其中一个袋子中取出一个球，发现它是蓝色的。计算它是从袋子 P 中取出的概率。

解决方案

设 E₁ 为选择袋子 P 的事件，E₂ 为选择袋子 Q 的事件，A 为取出蓝色球的事件。

然后，

P (E₁) = P (E₂) = ½

另外，

P(A/E₁) = P (从袋子 P 中取出蓝球) = 6/12 = ½

P(A/E₂) = P (从袋子 Q 中取出蓝球) = 3/6 = ½

使用贝叶斯定理，从 P 和 Q 两个袋子中取出蓝色球，且该球来自袋子 P 的概率如下。

示例 2

已知某人五次中有三次说真话。他掷骰子并报告他得到的数字是五。计算实际得到的数字是五的概率。

解决方案

设 A 为此人报告得到数字五的事件。

设 E₁ 为得到四的事件，E₂ 为其补事件。

那么，P (E₁) = 得到五的概率 = 1/6

P (E₂) = 没有得到五的概率 = 1 - P(E₁) = 1 - 1/6 = 5/6

另外，P (A/E₁) = 此人报告是五，且实际是五的概率 = 3/5

P (A/E₂) = 此人报告是五，但实际不是五的概率，

= 2/5

使用贝叶斯定理，实际得到的数字是五的概率是，