图的类型17 Mar 2025 | 4 分钟阅读 1. 空图: 空图定义为只包含孤立顶点的图。 示例: 图中所示的图是一个空图,并且顶点是孤立顶点。  2. 无向图: 无向图 G 由一组顶点 V 和一组边 E 组成。边集包含顶点的无序对。如果 (u, v)∈E,则称 u 和 v 由一条边连接,其中 u 和 v 是集合 V 中的顶点。 示例: 令 V = {1, 2, 3, 4} 且 E = {(1, 2), (1, 4), (3, 4), (2, 3)}。绘制该图。 答案: 该图可以以多种方式绘制。 其中两种如下:  3. 多重图: 如果图中允许在同一组顶点之间有多条边,则称之为多重图。换句话说,它是一个至少有一个环或多条边的图。  4. 有向图: 有向图或二分图 G 定义为无序对 (V, E),其中 V 是称为顶点的点集,E 是边集。图 G 中的每条边都被分配了一个方向,并被标识为一个有序对 (u, v),其中 u 是起始顶点,v 是结束顶点。 示例: 考虑图中所示的图 G = (V, E)。确定图 G 的顶点集和边集。  答案: 图 G =(V, E) 的顶点和边集如下: G={{1,2,3},{(1,2),(2,1),(2,2),(2,3),(1,3)}}。5. 无向完全图: 具有 n 个顶点的无向完全图 G=(V,E) 是一个图,其中每个顶点都连接到其他所有顶点,即,每对不同的顶点之间都存在一条边。它用 Kn 表示。具有 n 个顶点的完全图将有 示例: 绘制无向完全图 k4和 k6。 答案: k4 的无向完全图如图 1 所示,k6 的无向完全图如图 2 所示。  6. 连通图和非连通图 连通图: 如果从任意顶点 u 到 v 或反之存在一条路径,则称该图为连通图。 非连通图: 如果任意两个顶点之间不存在路径,则称该图为非连通图。 示例: 考虑图中所示的图。确定这些图是 (a)非连通图 (b)连通图。 另外,写出它们的连通分量。  解决方案 (i) 图中所示的图是一个非连通图,其连通分量为 {V1,V2,V3,V4},{V5,V6,V7,V8} 和 {V9,V10}。 (ii) 图中所示的图是一个非连通图,其连通分量为 {V1,V2},{V3,V4},{V5,V6},{V7,V8},{V9,V10} 和 {V11,V12}。  (iii) 图中所示的图是一个连通图。 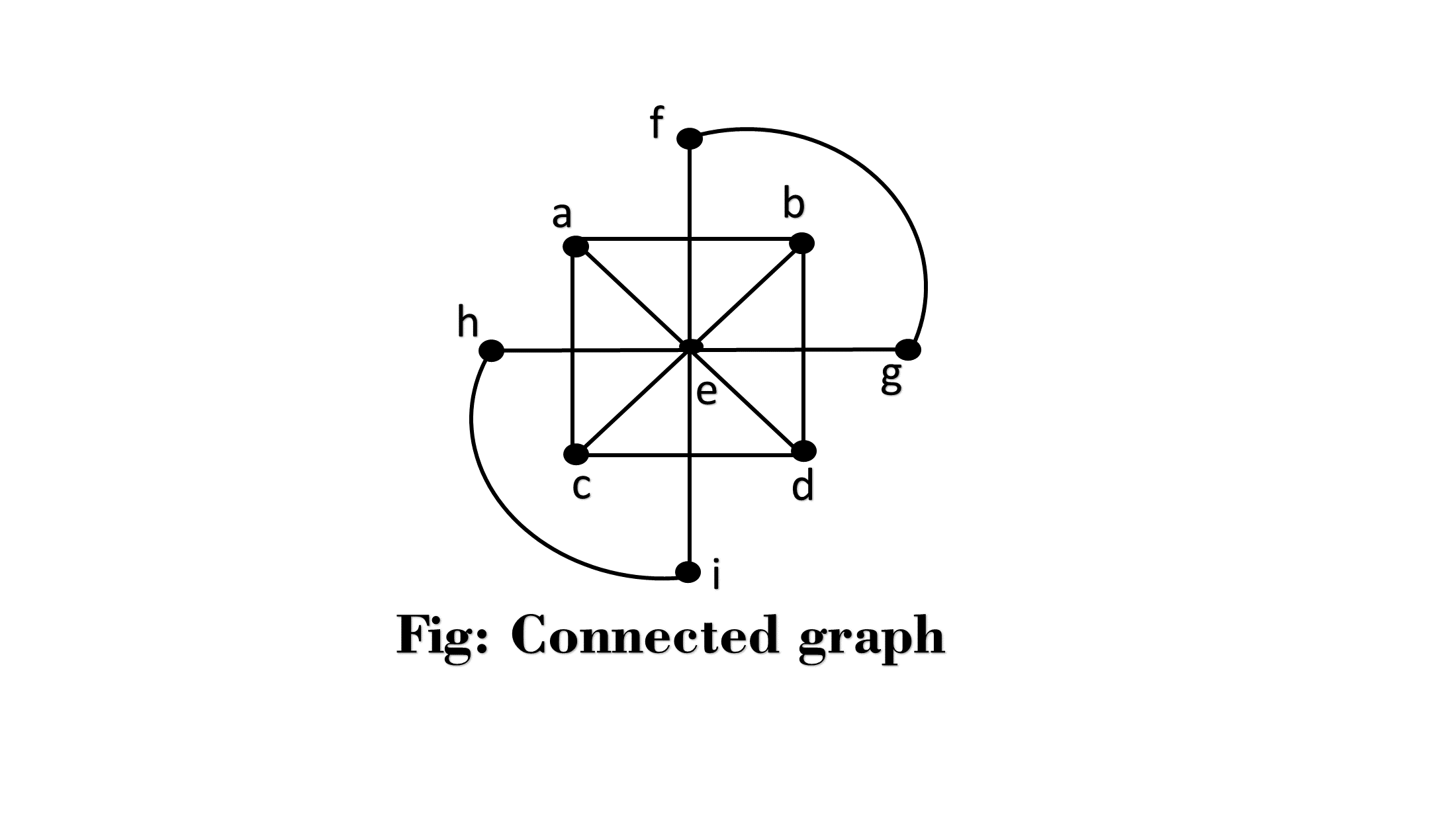 7. 连通分量: 图 G 的子图称为 G 的连通分量,如果它不包含在 G 的任何更大的连通子图中。它通过列出其顶点来定义。 示例: 考虑图中所示的图。确定其连通分量。  答案: 该图的连通分量是 {a, b, c}, {d, e, f}, {g, h ,i} 和 {j}。 8. 有向完全图: 具有 n 个顶点的有向完全图 G = (V, E) 是一个图,其中每个顶点都通过箭头连接到其他所有顶点。它用 Kn 表示。 示例: 绘制有向完全图 K3 和 K5。 答案: 将顶点的数量放置在适当的位置,然后从每个顶点到其他所有顶点绘制箭头,如图所示。   9. 补图: 图 G 的补图定义为一个具有与图 G 相同数量顶点的图,并且当且仅当两个顶点在图中不相关时,它们才被连接。 示例: 考虑图中所示的图 G。找到该图的补图。  答案: 上述图的补图如图所示。  10. 标记图: 如果图 G=(V, E) 的边用某个名称或数据进行标记,则称该图为标记图。因此,我们可以在其边集中用这些标签替换有序对。 示例: 图中所示的图是标记图。 G= {{a, b, c, d}, {e1,e2,e3,e4}}  11. 加权图: 如果图 G 的每条边都被分配了一个正数 w,称为边 e 的权重,则称图 G=(V, E) 为加权图。 示例: 图中所示的图是加权图。 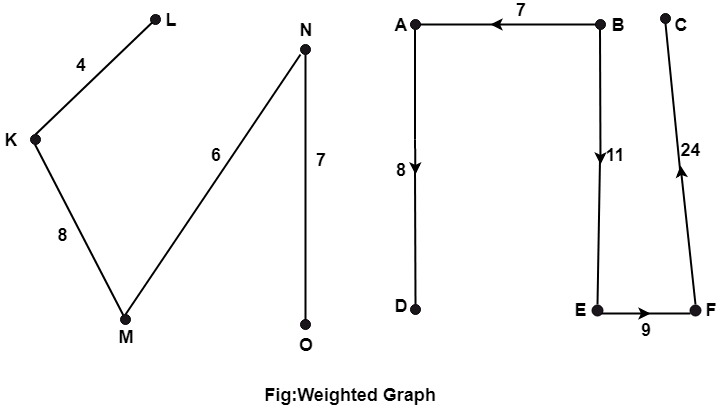 下一个主题图的表示 |
我们请求您订阅我们的新闻通讯以获取最新更新。