离散数学中的入度和出度

为了理解顶点的入度和出度，我们首先要了解顶点的度数的概念。之后，我们可以很容易地理解顶点的入度和出度。我们应该知道，入度和出度只能在有向图中确定。我们可以借助无向图计算顶点的度数。在无向图中，我们不能计算顶点的入度和出度。

顶点的度数

如果我们想找到图中每个顶点的度数，在这种情况下，我们必须计算一个特定顶点与其他顶点建立的关系数量。换句话说，我们可以通过计算连接到该顶点的边的数量来确定顶点的度数。顶点的度数用deg(v)表示。如果存在一个包含n个顶点的简单图，在这种情况下，任何顶点的度数将是

一个顶点能够与图中所有其他顶点形成一条边，除了它自己。所以在简单图中，顶点的度数将通过图中顶点的数量减去1来求得。这里的1是用于自环顶点，因为它不能自己形成一个环。如果图包含带有自环的顶点，那么那种类型的图将不是一个简单图。

示例

在这个例子中，我们有一个图，它有6个顶点，即a、b、c、d、e和f。顶点'a'的度数为5，所有其他顶点的度数为1。如果任何顶点的度数为1，那么那种类型的顶点将被称为“末端顶点”。

在两种情况下，我们可以考虑顶点的度数，如下所述：

• 无向图
• 有向图

现在我们将详细学习有向图中顶点的度数和无向图中顶点的度数。

无向图中顶点的度数

如果存在一个无向图，那么在这种类型的图中，将没有有向边。确定无向图中顶点度数的示例如下所述：

示例 1： 在此示例中，我们将考虑一个无向图。现在我们将找出该图中每个顶点的度数。

解决方案： 在上述无向图中，共有5个顶点，即a、b、c、d和e。每个顶点的度数如下所述：

• 上述图包含2条边，它们在顶点“a”处相交。因此，Deg(a) = 2
• 该图包含3条边，它们在顶点“b”处相交。因此，Deg(b) = 3
• 上述图包含1条边，它在顶点“c”处相交。因此，Deg(c) = 1。顶点c也称为悬挂顶点。
• 上述图包含2条边，它们在顶点“d”处相交。因此，Deg(d) = 2。
• 上述图包含0条边，它们在顶点“e”处相交。因此，Deg(a) = 0。顶点e也可以称为孤立顶点。

示例 2： 在此示例中，我们将考虑一个无向图。现在我们将找出该图中每个顶点的度数。

解决方案： 在上述无向图中，共有5个顶点，即a、b、c、d和e。每个顶点的度数如下所述：

顶点a的度数 = deg(a) = 2

顶点b的度数 = deg(b) = 2

顶点c的度数 = deg(c) = 2

顶点d的度数 = deg(d) = 2

顶点e的度数 = deg(e) = 0

在这个图中，没有悬挂顶点，顶点'e'是一个孤立顶点。

有向图中顶点的度数

如果图是有向图，那么在这个图中，每个顶点都必须有入度和出度。假设有一个有向图。在这个图中，我们可以使用以下步骤来找出顶点的入度、出度和度数。

顶点的入度

顶点的入度可以描述为以v为终点（terminal vertex）的边的数量，其中v表示终点。换句话说，我们可以将其描述为进入该顶点的边的数量。通过语法deg^-(v)，我们可以表示顶点的入度。如果我们想确定顶点的入度，为此，我们必须计算以该顶点为终点的边的数量。

顶点的出度

顶点的出度可以描述为以v为起点（initial vertex）的边的数量，其中v表示起点。换句话说，我们可以将其描述为从该顶点发出的边的数量。通过语法deg⁺(v)，我们可以表示顶点的出度。如果我们想确定顶点的出度，为此，我们必须计算从该顶点开始的边的数量。

顶点的度数

顶点的度数用deg(v)表示，它等于顶点的入度与出度之和。顶点的度数的符号表示如下：

示例 1： 在此示例中，我们有一个图，并且必须确定每个顶点的度数。

解决方案： 为此，我们首先将找出顶点的度数，顶点的入度，然后是顶点的出度。

正如我们所看到的，上面的图包含总共6个顶点，即v1、v2、v3、v4、v5和v6。

入度

顶点v1的入度 = deg(v1) = 1

顶点v2的入度 = deg(v2) = 1

顶点v3的入度 = deg(v3) = 1

顶点v4的入度 = deg(v4) = 5

顶点v5的入度 = deg(v5) = 1

顶点v6的入度 = deg(v6) = 0

出度

顶点v1的出度 = deg(v1) = 2

顶点v2的出度 = deg(v2) = 3

顶点v3的出度 = deg(v3) = 2

顶点v4的出度 = deg(v4) = 0

顶点v5的出度 = deg(v5) = 2

顶点v6的出度 = deg(v6) = 0

顶点的度数

根据上述定义，我们知道顶点的度数 Deg(v) = deg^-(v) + deg⁺(v)。现在我们将使用此公式进行计算，如下所示：

顶点v1的度数 = deg(v1) = 1+2 = 3

顶点v2的度数 = deg(v2) = 1+3 = 4

顶点v3的度数 = deg(v3) = 1+2 = 3

顶点v4的度数 = deg(v4) = 5+0 = 5

顶点v5的度数 = deg(v5) = 1+2 = 3

顶点v6的度数 = deg(v6) = 0+0 = 0

示例 2

在这个例子中，我们有一个有7个顶点的有向图。顶点“a”包含2条向外走的边，即“ad”和“ab”。因此，顶点“a”的出度为2。类似地，顶点“a”还有一条边“ga”，它指向顶点“a”。因此，顶点“a”的入度为1。

解决方案： 以上所有顶点的入度和出度如下所示：

入度

顶点a的入度 = deg(a) = 1

顶点b的入度 = deg(b) = 2

顶点c的入度 = deg(c) = 2

顶点d的入度 = deg(d) = 1

顶点e的入度 = deg(e) = 1

顶点f的入度 = deg(f) = 1

顶点g的入度 = deg(g) = 0

出度

顶点a的出度 = deg(a) = 2

顶点b的出度 = deg(b) = 0

顶点c的出度 = deg(c) = 1

顶点d的出度 = deg(d) = 1

顶点e的出度 = deg(e) = 1

顶点f的出度 = deg(f) = 1

顶点g的出度 = deg(g) = 2

每个顶点的度数

我们知道顶点的度数 Deg(v) = deg^-(v) + deg⁺(v)。现在我们将使用此公式进行计算，如下所示：

顶点a的度数 = deg(a) = 1+2 = 3

顶点b的度数 = deg(b) = 2+0 = 2

顶点c的度数 = deg(c) = 2+1 = 3

顶点d的度数 = deg(d) = 1+1 = 2

顶点e的度数 = deg(e) = 1+1 = 2

顶点f的度数 = deg(f) = 1+1 = 2

顶点g的度数 = deg(g) = 0+2 = 2

示例 3： 在此示例中，我们有一个有5个顶点的有向图。顶点'a'包含1条向外走的边，即'ae'。因此，顶点'a'的出度为1。类似地，顶点'a'还有一条边'ba'，它指向顶点'a'。因此，顶点'a'的入度为1。

解决方案： 以上所有顶点的入度和出度如下所示：

入度

顶点a的入度 = deg(a) = 1

顶点b的入度 = deg(b) = 0

顶点c的入度 = deg(c) = 2

顶点d的入度 = deg(d) = 1

顶点e的入度 = deg(e) = 1

出度

顶点a的出度 = deg(a) = 1

顶点b的出度 = deg(b) = 2

顶点c的出度 = deg(c) = 0

顶点d的出度 = deg(d) = 1

顶点e的出度 = deg(e) = 1

每个顶点的度数

我们知道顶点的度数 Deg(v) = deg^-(v) + deg⁺(v)。现在我们将使用此公式进行计算，如下所示：

顶点a的度数 = deg(a) = 1+1 = 2

顶点b的度数 = deg(b) = 0+2 = 2

顶点c的度数 = deg(c) = 2+0 = 2

顶点d的度数 = deg(d) = 1+1 = 2

顶点e的度数 = deg(e) = 1+1 = 2

示例 4： 在此示例中，我们有一个图，并且必须确定每个顶点的度数、入度和出度。

解决方案： 为此，我们首先将找出顶点的入度，然后是顶点的出度。

正如我们所看到的，上述图包含总共8个顶点，即0、1、2、3、4、5和6。

入度

顶点0的入度 = deg(0) = 1

顶点1的入度 = deg(1) = 2

顶点2的入度 = deg(2) = 2

顶点3的入度 = deg(3) = 2

顶点4的入度 = deg(4) = 2

顶点5的入度 = deg(5) = 2

顶点6的入度 = deg(6) = 2

出度

顶点0的出度 = deg(0) = 2

顶点1的出度 = deg(1) = 1

顶点2的出度 = deg(2) = 3

顶点3的出度 = deg(3) = 2

顶点4的出度 = deg(4) = 2

顶点5的出度 = deg(5) = 2

顶点6的出度 = deg(6) = 1

每个顶点的度数

我们知道顶点的度数 Deg(v) = deg^-(v) + deg⁺(v)。现在我们将使用此公式进行计算，如下所示：

顶点0的度数 = deg(0) = 1+2 = 3

顶点1的度数 = deg(1) = 2+1 = 3

顶点2的度数 = deg(2) = 2+3 = 5

顶点3的度数 = deg(3) = 2+2 = 4

顶点4的度数 = deg(4) = 2+2 = 4

顶点5的度数 = deg(5) = 2+2 = 4

顶点6的度数 = deg(5) = 2+1 = 3

图的度数序列

要确定图的度数序列，我们必须首先确定图中每个顶点的度数。之后，我们将这些度数按升序排列。这个顺序/序列可以称为图的度数序列。

例如： 在此示例中，我们有三个图，分别有3、4和5个顶点，所有图的度数序列都是3。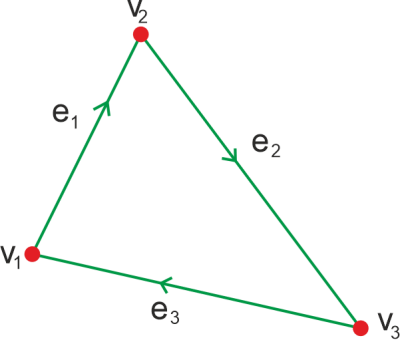

在上面的图中，有3个顶点。该图的度数序列如下所述：

<2, 2, 2>

在上面的图中，有4个顶点。该图的度数序列如下所述：

<2, 2, 2, 2>

在上面的图中，有5个顶点。该图的度数序列如下所述：

<2, 2, 2, 2, 2>