离散数学中的奇异矩阵

我们可以通过计算矩阵的行列式来判断给定矩阵是奇异矩阵还是非奇异矩阵。我们用符号 |A| 或 det A 来表示矩阵 A 的行列式。如果一个矩阵的行列式等于 0，则称该矩阵为奇异矩阵。在本节中，我们将学习奇异矩阵、如何识别奇异矩阵、它们的性质、奇异矩阵与非奇异矩阵的区别、示例以及更多内容。

什么是奇异矩阵

如果给定矩阵的行列式等于 0，则该奇异矩阵一定是一个方阵。换句话说，方阵 A 被称为奇异的，如果 det A = 0。我们知道，可以通过公式 A^-1 = (adj A) / (det A) 来找到矩阵 A 的逆。这里 det A 在分母上，用于表示 A 的行列式。我们知道，如果行列式等于 0，在这种情况下，我们无法定义这个分数。因此，我们无法定义矩阵 A 的逆 (A^-1)，如果 det A = 0。由于这个原因，将不存在任何矩阵 B 使得 AB = BA = I，其中 I 用于表示单位矩阵。

从以上解释可以清楚地看出，方阵 A 如果具有以下性质，则被称为奇异矩阵：

• det A = 0 (我们也可以写成 |A| = 0)
• A^-1 **未定义**（即 A 不可逆）

识别奇异矩阵

我们需要检查两个条件来识别给定矩阵是否为奇异矩阵，描述如下：

• 首先，我们将检查给定矩阵是否为方阵。
• 然后，我们将检查 det A = 0。

现在我们将展示一些示例，并确定给定矩阵是否为奇异矩阵。假设有一个矩阵 A，其中

该矩阵的阶数为 2*2。所以这是一个方阵。现在我们将按以下方式找到该矩阵的行列式：

|A| 或 det A = 3*4 ' 6*2 = 12 ' 12 = 0

该矩阵的行列式为 0。因此，该矩阵是方阵。

检查奇异矩阵的步骤

如果我们想知道给定矩阵是否为奇异矩阵，首先需要计算矩阵的行列式。这里我们将分别检查 2*2 矩阵和 3*3 矩阵。

对于 2*2 矩阵

在以下步骤中，我们将看到如何检查 3*3 矩阵是否为奇异矩阵。

步骤 1： 在此步骤中，我们将首先检查给定矩阵是否为方阵。

步骤 2： 2*2 矩阵包含 4 个元素（2 行 2 列）。因此，在此步骤中，矩阵 A 的行列式为 ad-bc。它用 |A| 或 det A 表示。

步骤 3： 在此步骤中，我们将检查行列式的值。如果行列式 ad-bc = 0，在这种情况下，矩阵 A 将被称为奇异矩阵。否则，我们将检查下一步。

步骤 4： 如果行列式 ad-bc ≠ 0，在这种情况下，矩阵 A 将被称为非奇异矩阵。

现在我们将通过一个例子来理解所有这些步骤。在此示例中，我们有一个 2*2 矩阵 A，其中

这是一个方阵。所以我们首先按照以下方式计算上述矩阵 A 的行列式：

|A| 或 det A = 3*4 ' 6*2

|A| = 12 ' 12

|A| = 0

这里 A 的行列式等于 0。因此，矩阵 A 是一个奇异矩阵。

对于 3*3 矩阵

在以下步骤中，我们将看到如何检查 3*3 矩阵是否为奇异矩阵。

步骤 1： 在此步骤中，我们将首先检查给定矩阵是否为方阵。

步骤 2： 3*3 矩阵包含 9 个元素（3 行 3 列）。因此，在此步骤中，矩阵 A 的行列式为 a1(b2c3 ' b3c2) ' a2(b1c3 ' b3c1) ' a3(b1c2 ' b2c1)。它用 |A| 或 det A 表示。

步骤 3： 在此步骤中，我们将检查行列式的值。如果行列式 {a1(b2c3 ' b3c2) ' a2(b1c3 ' b3c1) ' a3(b1c2 ' b2c1) = 0}，在这种情况下，矩阵 A 将被称为奇异矩阵。否则，我们将检查下一步。

步骤 4： 如果行列式 {a1(b2c3 ' b3c2) ' a2(b1c3 ' b3c1) ' a3(b1c2 ' b2c1) ≠ 0}，在这种情况下，矩阵 A 将被称为非奇异矩阵。

现在我们将通过一个例子来理解所有这些步骤。在此示例中，我们有一个 3*3 矩阵 A，其中

这是一个方阵。所以我们首先按照以下方式计算上述矩阵 A 的行列式：

|A| 或 det A = 0

A 的行列式等于 0。这是因为该矩阵的第一行和第二行相同。因此，矩阵 A 是一个奇异矩阵。

奇异矩阵的性质

在此，我们将根据奇异矩阵的定义来定义一些性质。这些性质描述如下：

• 如果存在一个奇异矩阵，那么它必须是一个方阵。
• 在奇异矩阵的情况下，如果我们计算行列式，它必须为零。
• 确定 2*2 阶矩阵行列式的公式将是 |A| = ad ' bc。
• 确定 3*3 阶矩阵行列式的公式将是 |A| = a1(b2c3 ' b3c2) ' a2(b1c3 ' b3c1) ' a3(b1c2 ' b2c1)。
• 我们不能定义奇异矩阵的逆，因此奇异矩阵是不可逆的。
• 如果存在一个任意阶数的零矩阵，那么它一定是一个奇异矩阵。
• 在奇异矩阵的情况下，所有行和列将不是线性独立的。
• 在奇异矩阵的情况下，该矩阵的秩必须小于其阶数。例如：如果存在一个 3*3 阶的奇异矩阵，那么它的秩将小于 3。
• 在矩阵的情况下，行列式有一些性质，描述如下：
  1. 如果一个矩阵中任意两行或任意两列相似，那么这种矩阵的行列式将为 0。因此它将是一个奇异矩阵。
  2. 如果一个矩阵中所有行和列的元素都为零，那么这种矩阵的行列式将为 0。因此它将是一个奇异矩阵。
  3. 当矩阵的一行（列）是另一行（列）的标量倍数时，该矩阵的行列式为 0。因此该矩阵是奇异矩阵。

奇异矩阵与非奇异矩阵

根据名称，非奇异矩阵不是奇异矩阵。因此，在非奇异矩阵的情况下，行列式将是非零数。换句话说，我们可以说，如果 det A ≠ 0，则方阵 A 被称为非奇异矩阵。我们可以在非奇异矩阵中定义矩阵的逆 (A^-1)，因为这种矩阵中总存在乘法逆。以下方式可以显示奇异矩阵与非奇异矩阵之间的区别：

奇异矩阵	非奇异矩阵
如果存在一个奇异矩阵 A，则该矩阵的行列式 det(A) 将为 0，即 **det(A) = 0**。	如果存在一个非奇异矩阵 A，则该矩阵的行列式 det(A) 将不等于 0，即 **det(A) ≠ 0**。
如果存在一个奇异矩阵 A，则我们**不能**定义其逆 A-1。	如果存在一个非奇异矩阵 A，则我们**可以**定义其逆 A-1。
在奇异矩阵的情况下，秩和阶数的关系如下：A 的秩 < A 的阶数	在非奇异矩阵的情况下，秩和阶数的关系如下：A 的秩 = A 的阶数
在奇异矩阵的情况下，某些行和列将是线性相关的。	在非奇异矩阵的情况下，所有行和列将是线性独立的。
如果存在一个奇异矩阵，则方程组 AX = B 将有无限多个解或无解。	如果存在一个非奇异矩阵，则方程组 AX = B 将有唯一解。
示例： 假设有一个奇异矩阵 A，其中 该矩阵的行列式如下所示：	示例： 假设有一个非奇异矩阵 A，其中 该矩阵的行列式如下所示：

生成奇异矩阵的定理

在奇异矩阵的情况下，有一个重要的定理用于生成奇异矩阵。根据该定理，如果存在两个矩阵 A 和 B，其中 A = [A]_n*k 且 B = [B]_k*n，则它们的乘积矩阵 AB，其阶数为 n*n，并且它将始终是奇异的。该定理表明：

• 两个矩阵 AB 的乘积将始终是奇异的，其中矩阵 A 的阶数为 n*1，矩阵 B 的阶数为 1*n。
• 两个矩阵 AB 的乘积也将是奇异的，其中矩阵 A 的阶数为 n*2，矩阵 B 的阶数为 2*n。

利用这个定理，我们可以将两个随机生成的阶数为 n*k 和 k*n 的矩阵相乘，并生成一个奇异矩阵。此处 n > k。

非奇异矩阵的示例

有许多非奇异矩阵的例子，其中一些描述如下：

示例 1： 在本例中，我们有两个矩阵，需要确定哪个矩阵是奇异矩阵。

解答： 要确定给定矩阵是否为奇异矩阵，我们必须逐一计算每个给定矩阵的行列式。

= -7*4 ' 2*(-14) = -28 + 28 = 0

该矩阵的行列式为 0。因此，这是一个方阵。现在我们将找到矩阵 (b) 的行列式。

= 2(0-6) + 1(1+12) + 3(3-0)

= -12 + 13 + 9

= 10 ≠ 0

因此，该矩阵的行列式不等于 0。因此，该矩阵不是奇异矩阵。

答案： (a) 是奇异矩阵，(b) 是非奇异矩阵。

示例 2： 在本例中，我们有一个矩阵 A，需要确定该矩阵是否为奇异矩阵。矩阵 A 的元素描述如下：

解答： 要确定给定矩阵是否为奇异矩阵，我们必须按照以下方式计算该矩阵的行列式。

det A = 1[(5*0) ' (4*2)] - 0[(0*0) ' (2* -1)] + (-3)[(0*4) ' (-1*5)]

|A| = (1 * -8) ' 0 + (-3 * 5)

|A| = -8 ' 15

|A| = -23 ≠ 0

因此，该矩阵的行列式不等于 0。因此，该矩阵不是奇异矩阵。

示例 3： 在本例中，我们有一个奇异矩阵 A，需要确定 k 的值。矩阵 A 的元素描述如下：

解答： 从问题中我们知道矩阵 A 是奇异矩阵。因此，其行列式将为 0。所以

(2*k) ' (-4*5) = 0

2k + 20 = 0

2k = -20

k = -20 /2

k = -10

因此，为了使 A 成为奇异矩阵，k 的值将为 -10。

示例 4： 在本例中，我们有一个奇异矩阵 A，需要确定 x 的值。矩阵 A 的元素描述如下：

解答： 从问题中我们知道矩阵 A 是奇异矩阵。因此，其行列式将为 0，即：

(x+1) (0-1) ' x(x+3-4) + 2(1-0) = 0

-x - 1 ' x^2 + x + 2 = 0

-x^2 + 1 = 0

x² = 1

x = ±1

因此，为了使 A 成为奇异矩阵，x = 1 或 -1。

示例 5： 在本例中，我们需要找出以下方程组是否具有唯一解。这些方程组描述如下：

2x + y + 2z = 3

x + z = 5

4x + y + 4z = 7

解答： 从问题中我们有三个方程组，可以通过相应的矩阵方程 AX+B 的形式将它们写成矩阵。进行此操作后，系数矩阵将变成这样：

当且仅当 A 的行列式不等于 0（即 A 是非奇异矩阵）时，该方程组才具有唯一解。所以我们将按此方式确定 A 的行列式：

= 2(0-1) - 1(4-4) + 2(1-0)

= -2 + 0 + 2

= 0

矩阵 A 的行列式为 0。因此，该方程组可能无解或有无穷多解。

因此，该方程组**不**具有唯一解。

示例 6： 在本例中，我们有一个奇异矩阵 A，需要确定 b 的值。矩阵 A 的元素描述如下：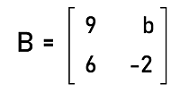

解答： 从问题中我们知道矩阵 A 是奇异矩阵。因此，其行列式将为 0。所以

(9* -2) ' (6*b) = 0

-18 ' 6b = 0

-6b = 18

b = 18 /-6

b = -3

因此，为了使给定的矩阵 A 成为奇异矩阵，b 的值将为 -3。

示例 7： 在本例中，我们有一个矩阵 P，需要确定该矩阵的逆。矩阵 P 的元素描述如下：

解答： 只有当给定矩阵不是奇异矩阵时，我们才能找到该矩阵的逆。这意味着该矩阵的行列式不应等于 0。从给定的矩阵中，我们有如下矩阵：

我们可以使用以下公式为非奇异矩阵确定矩阵 P 的逆：

P^-1 = adj P / |P|

因此，为了找到它，我们将按以下方式确定矩阵 P 的行列式：

|P| = (-3 * -8) ' (6*4)

|P| = 24 ' 24

|P| = 0

正如我们所见，矩阵 P 的行列式等于 0。因此它是一个奇异矩阵，并且该矩阵的逆不存在。