离散数学中的线性方程

如果方程中变量的最高幂为 1，则该方程称为线性方程。线性方程也称为一次方程。我们可以用一种方式表示一个变量的线性方程，即 Ax+B = 0。在这里，A 用于表示系数，x 用于表示变量，B 用于表示常数。还有一种方式可以表示具有两个变量的线性方程，即 Ax + By = C。在这里，A 和 B 用于表示系数，x 和 y 用于表示变量，C 用于表示常数。

什么是线性方程？

线性方程可以描述为最高次数为 1 的方程。这意味着线性方程不能包含指数大于 1 的变量。如果使用线性方程绘制图表，它将始终形成一条直线。

例如：假设有一个线性方程 y = 2x+1。现在我们将为此方程绘制一个图表，如下所示

正如我们所看到的，方程 y = 2x+1 的图表是一条直线。此图表中有一些点，描述如下

• 当上图中 x 增加时，y 增加两倍，因此我们需要 2x。
• 当此图中 x 为 0 时，y 已经为 1。因此我们还需要 +1。
• 所以：y = 2x+1

此图表的一些示例值描述如下

X y = 2x+1

-1 y = 2*(-1) + 1 = -1

0 y = 2*0 + 1 = 1

1 y = 2*1 + 1 = 3

2 y = 2*2 + 1 = 5

我们可以检查所有这些点是否都是上面所示直线的一部分。

线性方程的定义

方程也可以称为一种数学语句，它能够在代数表达式之间包含等号 (=)。这类方程必须包含 1 次幂。当我们将其绘制在图表上时，它总是形成一条直线。因此，这类方程可以称为“线性方程”。有三种表示线性方程的方法，即一个变量的线性方程、两个变量的线性方程和三个变量的线性方程。

在线性方程的求解过程中，将生成一些值，当我们用这些值替换未知值时，这些值将使给定方程成立。例如：假设我们有一个方程 x+2 = 0。这个方程只能提供一个解，即 x = -2。但是如果有一个两个变量的线性方程，那么对于它，解将以欧几里得平面中点的笛卡尔坐标形式计算。现在我们将展示一些方程并识别哪些是线性方程，哪些是非线性方程。

线性方程的公式

借助线性方程的公式，我们可以表达一个线性方程。有多种方法可以做到这一点。例如：我们可以以各种方式表达线性方程，例如斜截式、标准式或点斜式。现在我们将学习如何借助学习线性方程的标准式来表达线性方程。线性方程的公式取决于方程中变量的数量。我们还应该记住，方程中所有变量的最高次数必须为一。

线性方程的形式

有多种形式可以表示线性方程，描述如下

1. 标准式
2. 斜截式
3. 点斜式
4. 作为函数
5. 恒等函数
6. 常数函数

现在我们将逐一详细学习它们，如下所示

1. 线性方程的标准式

有三种方式可以写线性方程，即一个变量形式、两个变量形式和三个变量形式。一个变量形式也称为标准形式。

一个变量的线性方程的标准式或一般式可以写成以下形式

这里 A 和 B 用于表示实数，x 用于表示变量。

两个变量的线性方程的标准式可以写成以下形式

这里，x 和 y 用于表示变量，A、B 和 C 用于表示实数或常数。

三个变量的线性方程的标准式可以写成以下形式

这里，x、y 和 z 用于表示变量，A、B、C 和 D 用于表示实数，使得 A ≠ 0，B ≠ 0，C ≠ 0。

2. 斜截式

斜截式是表示线性方程最常见的一种形式，描述如下

y= mx+b

此处，

m 用于表示直线的斜率

x 和 y 分别用于表示 x 轴和 y 轴的坐标。

b 用于表示 y 轴截距。

直线的斜截式方程在以下图中描述

例如： y = 3x + 7

斜率 m = 3，截距 b = 7。

如果有一条直线平行于 x 轴，在这种情况下，x 坐标将为零。因此，

如果有一条直线平行于 y 轴，在这种情况下，y 坐标将为零。

斜率：我们可以通过计算 y 坐标的变化与 x 坐标的变化之比来确定直线的斜率。m 用于表示斜率。以下公式用于计算斜率

所以基本上，斜率用于表示平面中线的上升以及在 x 轴上覆盖的距离。我们也可以将直线的斜率称为梯度。

3. 点斜式

如果我们考虑 x-y 平面中的点，那么我们可以以线性方程的形式形成一个直线方程，描述如下

其中 (x1, y1) 用于表示点的坐标。

还有一种表示方式，描述如下

直线的点斜式方程在以下图中描述

4. 作为函数

a) 有时，我们可以借助 f(x) 而不是 y 来将线性方程写成函数形式。

例如

y = 5x - 9

f(x) = 5x - 9

上面两个方程是相同的。

b) 我们不能总是借助 f(x) 来写函数。

例如

y = 5x - 9

w(u) = 5u - 9

h(z) = 5z - 9

上面三个方程也是相同的。

5. 恒等函数

线性方程包含一种特殊类型的函数，称为恒等函数。以下语法用于表示恒等函数，描述如下

f(x) = x

恒等函数的图表描述如下

上面的图表创建一个 45° 角，其斜率为 1。

在恒等函数的情况下，输入值和输出值将始终相同。这意味着我们作为输入输入的值将得到相同的输出值。这就是它被称为恒等的原因。

6. 常数函数

还有一种特殊类型的线性函数，称为常数函数。此函数总是绘制一条水平线。以下语法用于表示常数函数，描述如下

f(x) = C

常数函数的图形表示如下

在常数函数中，f(x) 将始终等于常数值。在这种情况下，x 的值将无关紧要。它也等于一个常数值。

总结

线性方程可以写成许多不同的形式，其中一些描述如下

其中 m 用于表示直线的斜率，(a, b) 用于截取 x 轴和 y 轴。

线性方程的图表

如果存在一个只有一个变量的线性方程，那么它将在图表中形成一条垂直线，并且该类型的线将平行于 y 轴，反之亦然。如果存在一个具有两个变量的线性方程，那么它将在图表中形成一条直线。现在我们将通过一些示例绘制一个具有两个变量的线性方程的图表，描述如下

示例：这里，我们有一个两个变量的线性方程 x - 2y = 2。我们将为此方程绘制一个图表。

我们将使用一些步骤在图表中绘制线性方程，描述如下

步骤 1：在此步骤中，我们有一个线性方程 x - 2y = 2。

步骤 2：现在，我们将使用形式 y = mx+b 并将给定方程转换为此形式。转换后，我们将得到 y = x/2 -1

步骤 3：在此步骤中，我们将 x 的值替换为不同的数字，这些替换的结果将以 y 的形式获得以创建坐标。

步骤 4：在此步骤中，我们将 x = 0 放入上述方程 y = x/2 -1。之后，我们将得到 y = 0/2 -1，即 y = -1。同样，如果我们将 x 的值设为 2 放入同一方程中，那么我们将得到 y = 2/2 -1，即 y = 0。

步骤 5：在此步骤中，我们将 x 的值设为 4 放入方程 y = x/2 -1。放入后，我们将得到 y = 4/2 -1，即 y = 1。类似地，如果我们将 x 的值设为 -2 放入同一方程中，那么我们将得到 y = -2/2 -1，即 y = -2。现在，线性方程 y = x/2 -1 将由这些值对 (x, y) 满足。在下表中，我们可以显示所有坐标的列表。

步骤 6：在最后一步，我们将在图表上绘制所有上述点 (4, 1)、(2, 0)、(0, -1) 和 (-2, -2)，当我们连接它们时，我们将得到一条直线。借助以上步骤，我们可以在图表上显示一个线性方程。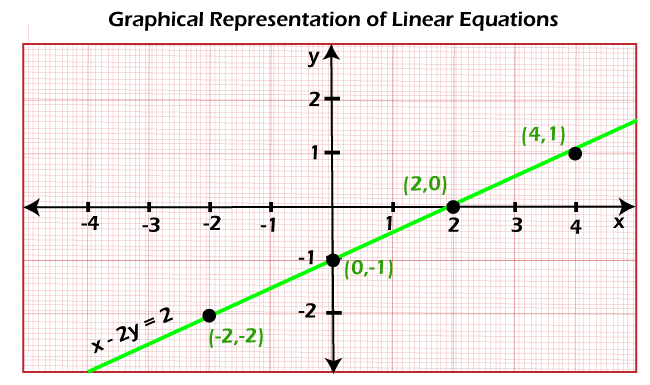

一个变量的线性方程

一个变量的线性方程可以描述为只包含一个变量的方程。这类方程必须是 Ax + B = C 的形式。这里，x 用于表示只包含一个解的未知变量，A、B 用于表示实数。通过这种方式，我们可以很容易地表示一个数学语句。线性方程的次数必须等于 1。

一个方程总是有两边，两边必须平衡才能求解线性方程。方程的等号用于表示表达式的两边相等。求解只包含一个变量的线性方程非常容易。我们可以通过分离变量和常数来获得未知变量的值。我们将变量放在方程的一边，常数组合起来放在方程的另一边。之后，我们将对两边进行一些操作，使方程的平衡不受影响。

示例 1：这里，我们必须求解一个具有一个变量的线性方程，即 2x + 5 = 23。

解：如果我们把变量放在 LHS，数字放在 RHS，就可以解这个方程。这意味着我们将按以下方式进行方程求解，例如 2x = 23-5。现在，我们将求解 x 的值并得到 2x = 12。最后，我们将得到 x 的值为 x = 12 /2 = 6。

示例 2：这里，我们必须求解一个具有一个变量的线性方程，即 (2x-10) /2 = 3(x-1)。

解：我们将借助一些步骤来解决这个问题，描述如下

步骤 1：首先，我们将清除分数，如下所示

(2x-10) / 2 = 3(x-1)

x - 5 = 3(x-1)

步骤 2：现在，我们将简化方程的两边，如下所示

x - 5 = 3x-3

x = 3x+2

步骤 3：现在，我们将分离 x，如下所示

x - 3x = 2

-2x = 2

x = -1

两个变量的线性方程

一个包含两个变量的线性方程可以描述为 Ax + By + C = 0 的形式。其中，x 和 y 表示两个变量，每个变量的次数均为 1，A、B 和 C 表示实数。A、B 和 C 的值不能等于零。如果存在两个这样的线性方程，那么该方程将被称为联立线性方程。例如： 5x + 3y + 17 = 0

对于一个方程可以有无限多的解。如果我们想找到两个变量的值，那么我们必须选择一组两个方程，例如 Ax + By + C = 0 和 Dx + Ey + F = 0。这里，A、B、C、D、E 和 F 用于表示常数，并且 A、B、D 和 E 必须不等于零。

例如：这里，我们必须解方程 x+5y = 7 和 x = y。

解：根据问题，我们有两个方程，

x+5y = 7 ?? (1)

x = y ??? (2)

现在我们将方程 2 的值代入方程 1，得到以下结果

? y+5y = 7

? 6y = 7

? y = 7/6

? x = y = 7/6

三个变量的线性方程

如果我们想找到三个未知数的值，那么我们必须选择一组三个方程。我们可以借助最流行的方法之一，即矩阵法，来求解具有三个变量的线性方程。

A1x + B1y + C1z + D1 = 0

A2x + B2y + C2z + D2 = 0 和

A3x + B3y + C3z + D3 = 0

其中

A1, A2, A3, B1, B2, B3, C1, C2, C3, D1, D2, 和 D3 用于表示实数，其中 A1, A2, A3, B1, B2, B3, C1, C2, C3 必须不等于零。这里，x, y, 和 z 用于表示变量。

例如：这里，我们必须求解三个变量的线性方程

x+3y-2z = 10

2x-y+6z = 3

x+y-2z = 5

解：根据以上问题，我们有三个方程。所以我们可以使用以下矩阵来写这些方程，如下所示

AX = B

现在我们必须找到这个矩阵的逆矩阵，这样我们就可以确定矩阵 X，如下所示

X = A^-1B

这里我们将按如下方式计算矩阵 A 的行列式

|A| = 1(2-6) -3(-4 - 6) -2(2+1)

= -4 -3(-10) -2(3)

= -4 + 30 - 6

= 20

现在我们将按如下方式确定矩阵 A 的伴随矩阵

现在 A^-1 = (adj A) /|A|

A^-1 =

X = A^-1B

=>

因此，上述方程的解描述如下

X = 60 /23

Y = 57 /23

Z = 1 /23

如何求解线性方程

一个方程可以被描述为一个加权平衡，两边具有相同数量的权重。如果我们从方程的左侧和右侧添加或减去相同的数字，则给定方程仍然是正确的或不会受到影响。同样，如果我们将方程的左侧和右侧乘以或除以相同的数字，则方程是正确的。为了求解线性方程，我们将所有常数放在一边，变量放在另一边，然后我们将尝试确定未知变量的值。通过这个过程，我们可以求解一个变量的线性方程。现在，我们将借助一个示例来理解这个概念，描述如下

示例：这里，我们必须求解方程 5x-3 = 7。

现在我们将对等式（即LHS和RHS）的两侧进行一些数学运算，这样它的平衡就不会被破坏。我们将通过在等式的LHS和RHS都加上3来将LHS简化为5x。由于这种加法，等式的平衡不会被破坏。所以新的LHS将是5x - 3 + 3 = 5x，新的RHS将是7 + 3 = 10。现在我们将通过将等式两侧除以5来将LHS简化为x。因此，我们得到x = 2。通过这种方式，我们可以求解一个变量的线性方程。

重要提示

在学习线性方程时，有一些重要点需要注意，描述如下

• 如果给定变量的值有助于使线性方程为真，那么这些值将被称为线性方程的根或解。
• 如果我们在给定方程的左右两边同时进行加、减、乘、除相同的数，那么线性方程的解将不受影响。
• 线性方程总是以直线的形式绘制图表，无论是单变量还是双变量。

线性方程示例

线性方程有多种示例，其中一些描述如下

示例 1：在此示例中，我们有一个线性方程 x = 16(x+5)，我们必须求解它。

解：根据问题，我们有一个方程 x = 16(x+5)

x = 16x + 75

现在我们从上述方程的两边减去 75，如下所示

x - 75 = 16x+75-75

x - 75 = 16x

15x = -75

x = -75/15

x = -5

因此，x 的值为 -5。

示例 2：在此示例中，我们有两个方程，x-y = 12 和 2x+y = 22，我们必须求解它们。

解：根据问题，我们有两个方程

x - y = 12 ....... (1)

2x + y = 22 ....... (2)

现在我们将方程 (1) 中的 x 分离出来，如下所示

x = y+12 ......... (3)

现在我们将方程 (3) 代入方程 (2)，如下所示

2(y+12) + y = 22

3y+24 = 22

3y = -2

y = -2/3

现在我们将 y 的值代入 x = y+12，如下所示

x = y+12

x = -2/3 + 12

x = 34/3

因此，x 的值为 34/3，y 的值为 -2/3

示例 3：在此示例中，我们有一个线性方程 5x - 95 = 75，我们必须求解它。

解：根据问题，我们有一个方程 5x-95 = 75。

5x = 75+95

5x = 170

x = 170/5

x = 34

因此，x 的值为 34。

示例 4：在此示例中，一个数的十倍等于 50。这里，我们必须建立一个线性方程并确定未知数的值。

解：为此，我们将假设未知数是 x。根据问题，我们知道这个数的十倍等于 50。这意味着 10x = 50。这个方程是一个有一个变量的线性方程，我们可以求解 x 的值，它是未知数。所以，

10x = 50

x = 50/10

x = 5

因此，未知数 = 5。

示例 5：在此示例中，两个数的和为 32。这里，如果一个数比另一个数多 8 倍，我们必须通过建立一个线性方程来确定这两个数。

解：这里，我们假设第一个数是 x，那么根据问题，第二个数将是 x+8。现在我们可以借助这些值形成一个线性方程，描述如下

x + x+8= 32

2x+8 = 32

现在我们将通过将变量放在一边，常数放在另一边来求解上述线性方程，如下所示

2x = 32-8

现在我们将简化 RHS 并得到以下结果

2x = 24

x = 24 /2

x = 12

这意味着我们的第一个数是 12。所以，第二个数将是

12 + 8

= 20

因此，我们的两个数是 12 和 20。