卡诺图

卡诺图是一个平面区域，被划分为 2ⁿ 个相等的单元格，每个单元格代表一个点 用于 n 个变量的函数。 每个变量 x 用于以不同的方式将区域分成两个相等的部分，即一个用于 x，另一个用于 x'。与函数值为 1 的参数相对应的单元格包含 1。

示例 1： 当变量数 n = 1 时，卡诺图如图所示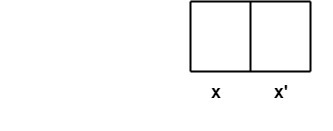

2. 当变量数 n = 2 时，卡诺图如图所示

3. 当变量数 n = 3 时，卡诺图如图所示

使用 K-Map 简化布尔函数

布尔函数可以使用 k-map 简化。它基于组合相邻单元格中的项的原理。如果两个单元格仅在一个变量中不同，则称它们是相邻的。在相邻的单元格中，其中一个变量是相同的，而另一个变量在一个单元格中以非补码形式出现，在另一个单元格中以补码形式出现。

SOP 形式的最小化

可以使用以下算法来获得最小化的表达式

1. 识别不能与任何其他 1 组合的 1，并将其圈起来。
2. 识别只能以一种方式组合成两组的 1，并将它们圈起来作为组。
3. 识别可以与其他三个 1 组合，以形成四个相邻 1 的组，并且只有一种方式，并将它们圈起来作为组。
4. 识别可以与其他七个 1 组合，以形成八个相邻 1 的组，并且只有一种方式，并将它们圈起来作为组。
5. 在识别出 2、4 和 8 个 1 的基本组之后，如果仍然存在一些尚未被圈起来的 1，那么这些 1 应该彼此组合或与其他已经被圈起来的 1 组合，也就是说，我们应该将剩余的 1 连接到尽可能大的组中，并尽可能少的进行分组。

示例 1： 使用 k-map 最小化以下布尔表达式

              f(A, B) = A' B+BA

解决方案： 首先画出 2 变量的 k-map，并在相应的单元格中插入 1，如图所示

所需的最小化布尔表达式为 f=B。

示例 2： 使用 k-map 最小化以下布尔表达式

              AB + A' B+BA'

解决方案： 画出两变量的 k-map，并在相应的单元格中插入 1，如图所示

所需的最小化布尔表达式为 f=A+B。

示例 3： 使用 k-map 最小化以下布尔表达式

              f(A, B, C) = AB' C+A' BC+AB+A' B' C

解决方案： 画出 3 变量的 k-map，并在相应的单元格中插入 1，如图所示

所需的最小化布尔表达式为 f=AB+C'

最小化不在最小项/最大项中的布尔函数

最小化此类函数的一种方法是将它们转换为标准形式，即 SOP 或 POS，然后制作 k-map 并获得最小化的函数。

另一种方法是直接使用以下算法准备 k-map

1. 最小项输入 1，最大项输入 0。
2. 对于每个项，其变量数比变量总数少 1，则输入一对 1/0。
3. 对于变量数比变量总数少 2 的项，则输入四个相邻的 1/0。
4. 以类似的方式重复其他项。

示例： 最小化四变量逻辑函数

              f (A, B, C, D) = A B C'D + A' BCD+A' B' C'+A' B' D'+AC'+AB' C+B'

解决方案： k-map 的获取方式如下

(a) 在单元格 A=1、B=1、C=0、D=1 中输入 1，对应于最小项 A B C'D

(b) 在单元格 A=0、B=1、C=1、D=1 中输入 1，对应于最小项 A' BCD

(c) 在单元格 A=0、B=0、C=0 中输入 2 个 1，对应于项 A' B' C'

(d) 在单元格 A=0、B=0、D=0 中输入 2 个 1，对应于项 A' B' D'

(e) 在单元格 A=1、B=0、C=1 中输入 2 个 1，对应于项 AB' C

(f) 在单元格 A=1、C=0 中输入 4 个 1，对应于项 AC'

(g) 在单元格 B=0 中输入 8 个 1，对应于项 B'