杜立特尔算法：LU分解

在本节中，我们将借助杜利特尔算法学习矩阵的 LU 分解。这里 LU 也可以被称为“LU 因式分解”，其中 LU 代表“下三角-上三角”。1938 年，著名数学家 Tadeusz Banachiewicz 提出了 LU 分解。在杜利特尔算法中，我们将在数值分析和线性分析中将矩阵分解为下三角矩阵和上三角矩阵的乘积形式。借助 LU 分解，计算机可以求解线性方程组的方阵。在计算矩阵行列式或求逆矩阵时，这将是关键一步。

假设有一个方阵 A。LU 因式分解可以描述为 A 的因式分解，带有适当的列和/或行的置换或顺序，它将分为两个因子，即由 L 表示的下三角矩阵和由 U 表示的上三角矩阵。因此 A = LU。

杜利特尔算法

方阵可以很容易地分解为下三角矩阵和上三角矩阵，描述如下：

我们还有一种方法可以将 A 分解为 LU 分解，即杜利特尔方法。这种方法允许我们进行分解，而无需进行高斯消元法的麻烦。

假设有一个 n * n 矩阵 A。这里我们将假设这个矩阵也包含 LU 分解，我们将明确地写出 L 和 U 的形式。之后，我们将使用系统的方法，借助 A = LU 所需乘法产生的方程来求解 L 和 U 中的元素。

用于 U 矩阵的项描述如下：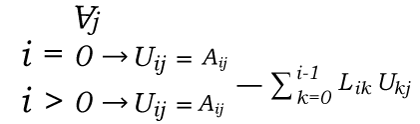

而用于 L 矩阵的项描述如下：

LU 分解的例子

示例 1

输入

输出

例 2： 在此示例中，我们将借助杜利特尔方法求给定矩阵的 LU 分解。

解： 根据杜利特尔算法，

A = LU

所以

以上矩阵意味着

u₁₁ = 8

u₁₂ = -6

u₁₃ = 2

I₂₁u₁₁ = -6 ⇒ I₂₁ * 8 = -6 ⇒ I₂₁ = -3/4

I₂₁u₁₂ + u₂₂ = 7 ⇒ (-3/4) * (-6) + u₂₂ = 7 ⇒ u₂₂ = 5/2

I₂₁u₁₃ + u₂₃ = -4 ⇒ (-3/4) × 2 + u₂₃ = -4 ⇒ u₂₃ = -5/2

l₃₁u₁₁ = 2 ⇒ l₃₁ × 8 = 2 ⇒ l₃₁ = 1 / 4

l₃₁u₁₂ + l₃₂u₂₂ = -4 ⇒ 1/4 × (-6) + l₃₂ × 5/2 = -4 ⇒ l₃₂ = -1

l₃₁u₁₃ + l₃₂u₂₃ + u₃₃ = 3 ⇒ 1/4 × 2 + (-1) × (-5/2) + u₃₃ = 3 ⇒ u₃₃ = 0

A = L * U = LU

杜利特尔方法

这里我们将描述杜利特尔方法 LU 分解 A 的步骤，当下三角矩阵 L 的对角线元素为单位值时。

步骤：

1. 首先，我们将创建矩阵 A、B 和 X。其中 A 用于表示增广矩阵，B 用于表示常数，X 用于构成变量向量。
2. 假设 A = LU，其中 U 用于表示上三角矩阵，L 用于表示下三角矩阵。假设 L 的对角线元素等于 1。
3. 假设 Ly = B。现在我们将求解 y。
4. 假设 Ux = y。现在我们将求解变量向量 x。

示例

X₁ + X₂ + X₃= 5

X₁ + 2X₂ + 2X₃ = 6

X₁ + 2X₂+ 3X₃ = 8

解决方案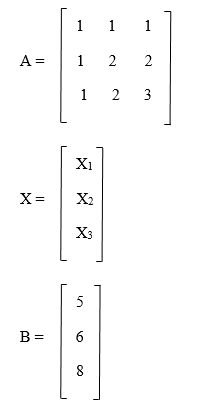

假设 A = LU。所以，

假设 Ly = B

Y₁ = 5

Y₁ + Y₂ = 6; Y₂ = 1

Y₁ + Y₂ + Y₃ = 8; Y₃ = 2

Y₁ = 5 Y₂ = 1 Y₃ = 2

假设 Ux = Y