离散数学中的行矩阵

如果一个矩阵只包含一行，那么它就被称为行矩阵。但在行矩阵的情况下，列可以有一个或多个元素。通过 1*n 的阶数，我们可以表示行矩阵的阶数。这里 1 表示行数，n 表示列数。在任何矩阵中，行和列都用于容纳元素。我们可以通过水平排列来表示行元素。假设有一个矩阵 B = [bij]，其阶数为 1*n。行矩阵将表示如下

例如

X = [4 6]_1∗2

Y = [x y z]_1∗3

Z = [4 6 1 9]_1∗4

在本节中，我们将学习行矩阵、它们的定义、性质、运算以及行矩阵的示例。

什么是行矩阵

行矩阵是一种矩阵，其中所有元素都排列在单行中。也就是说，在行矩阵中，可以有多个列，但只有一行。假设有一个 m*n 矩阵，其中 m 表示行数，n 表示列数。在此阶数中，如果 m = 1，则此类型的矩阵将被称为行矩阵。因此，我们可以借助水平排列的元素来形成行矩阵。

行矩阵可以描述为一种矩形排列的元素，这些元素以水平线的形式排列。以下方式表示行矩阵的通用表示

换句话说，我们可以这样写

我们无法定义行矩阵的行列式，因为行矩阵不是方阵。如果矩阵的阶数为 1*1，即行数和列数都为 1，那么我们才能找到行矩阵的行列式。如果阶数为 1*n 且 n 大于 1，我们则无法定义行矩阵的行列式。现在我们将展示一些例子，以便我们更好地理解行矩阵的概念。

行矩阵的性质

我们可以通过一些性质来深入理解行矩阵的概念，它们描述如下

• 行矩阵只包含一行。
• 行矩阵可以包含多列。
• 行矩阵中的元素数量与矩阵的列数相同。
• 行矩阵也称为矩形矩阵。
• 当我们对行矩阵进行转置时，我们将得到列矩阵作为结果。
• 我们只能通过列矩阵来乘出行矩阵。
• 如果我们乘以列矩阵和行矩阵，我们将得到一个单例矩阵。

行矩阵运算

在离散数学领域，可以对行矩阵执行各种运算，即乘法、减法、加法和除法。在执行加法和减法运算时，我们可以取任何其他矩阵进行运算。如果是一个行矩阵，那么我们只能对任何其他行矩阵执行加法和减法运算。对于行矩阵的加法或减法运算，这些矩阵的阶数必须相同。行矩阵加法的例子如下

A = [4 -7 1 2], B = [3 9 5 2]

A+B = [4+3 (-7)+9 1+5 2+2] = [7 2 6 4]

行矩阵减法的例子如下

A = [5 8 3 1], B = [3 2 7 9]

A-B = [5-3 8-2 3-7 1-9] = [2 6 -4 -8]

通过列矩阵，我们可以实现行矩阵的乘法。对于矩阵乘法，我们必须满足其条件，即第一个矩阵的列数和第二个矩阵的行数必须相同。也就是说，在乘法运算的情况下，行矩阵的列数和列矩阵的行数必须相同。两个矩形矩阵乘法的例子如下

当我们通过列矩阵乘以前一个行矩阵时，生成的结果将是一个单例矩阵。如果我们想要行矩阵的逆，那是不可能的，因此，我们不能对行矩阵进行除法运算。也就是说，行矩阵可以进行加法、减法和乘法，但不能进行除法。

按阶数划分的行矩阵示例

这里我们将展示不同阶数的行矩阵，它们描述如下

示例 1：在此示例中，我们将展示一个阶数为 1*1 的行矩阵，描述如下

A = [7]_1∗1

在此矩阵中，我们可以看到只有一个元素，它排列成 1 行 1 列。在矩阵 A = [7] 中，行列式为 7。

示例 2：在此示例中，我们将展示一个阶数为 1*2 的行矩阵，描述如下

A = [3 7]_1∗2

在此矩阵中，我们可以看到有两个元素，它们排列成 1 行 2 列。因此，我们可以说它是一个行矩阵。

示例 3：在此示例中，我们将展示一个阶数为 1*3 的行矩阵，描述如下

A = [4 6 8]_1∗3

在此矩阵中，我们可以看到有三个元素，它们排列成 1 行 3 列。

示例 4：在此示例中，我们将展示一个阶数为 1*4 的行矩阵，描述如下

A = [2 5 6 9]_1∗4

在此矩阵中，我们可以看到有四个元素，它们排列成 1 行 4 列。

示例 5：在此示例中，我们将展示一个阶数为 1*5 的行矩阵，描述如下

A = [1 4 7 8 3]_1∗5

在此矩阵中，我们可以看到有五个元素，它们排列成 1 行 5 列。

示例 6：在此示例中，我们将展示一个阶数为 1*6 的行矩阵，描述如下

A = [5 6 3 9 1 4]_1∗6

在此矩阵中，我们可以看到有六个元素，它们排列成 1 行 6 列。

以上所有示例都称为行矩阵，因为这些矩阵的所有元素都排列在单行中，但在多列中。

行矩阵示例

有很多行矩阵的例子，其中一些描述如下

示例 1：在此示例中，我们有一个行矩阵，并且需要转置该矩阵。行矩阵描述如下

[3 4 1]

解答：根据题目，我们有一个行矩阵 A，其中

A = [3 4 1]

我们可以通过将行矩阵的所有元素写成列元素的形式来执行行矩阵的转置。

因此，列矩阵是行矩阵的转置。

示例 2：在此示例中，我们有一个行矩阵 [1 2 -1] 和一个列矩阵，并且需要将这两个矩阵相乘。列矩阵描述如下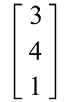

解答：根据题目，我们有行矩阵和列矩阵如下

行矩阵与列矩阵的乘法描述如下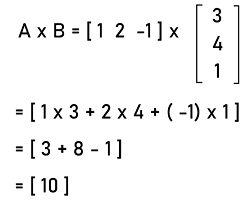

因此，行矩阵与列矩阵的乘积是一个单例矩阵。

重要提示

在学习行矩阵概念时，有很多需要记住的要点，它们描述如下

• 如果一个矩阵的所有元素都排列成单行，则该矩阵可以定义为行矩阵。
• 行矩阵只包含一行，但可以包含多列。
• 行矩阵可以用阶数 1*n 表示。
• 行矩阵可以描述为一种矩形排列的元素，并且水平方式用于排列行矩阵的所有元素。
• 我们可以使用以下表达式在数学上表示行矩阵
• A = [a11 a12 a13 .... a1n]_1∗n
• 行矩阵转置的结果将是一个列矩阵。
• 只有当两个行矩阵具有相同的阶数时，才能对这两个矩阵进行加法和减法。
• 通过列矩阵，我们可以执行行矩阵的乘法。
• 当我们对两个矩阵，即行矩阵和列矩阵进行乘法时，我们将得到一个单例矩阵作为结果。
• 我们不能对行矩阵进行求逆运算，因此我们不能对行矩阵执行除法运算。