生成树

连通图 G 的子图 T 称为 G 的生成树，如果 T 是树并且 T 包含 G 的所有顶点。

最小生成树

假设 G 是一个连通加权图，即 G 的每条边都分配了一个非负数，称为边的权重，那么 G 的任何生成树 T 都被分配一个总权重，该总权重通过将 T 中边的权重相加得到。

G 的最小生成树是一棵总权重尽可能小的树。

Kruskal 算法查找最小生成树： 该算法查找给定连通加权图 G 的最小生成树 T。

1. 输入具有 n 个顶点的给定连通加权图 G，我们想要找到其最小生成树 T。
2. 根据权重的增加顺序对图 G 的所有边进行排序。
3. 使用所有顶点初始化 T，但不包括任何边。
4. 将每个图 G 添加到 T 中，该图不形成循环，直到添加了 n-1 条边。

示例 1： 确定图中所示的加权图的最小生成树

解决方案： 使用 kruskal 算法按增加的顺序排列加权图的所有边，并使用 G 的所有六个顶点初始化生成树 T。现在开始将 G 的边添加到 T 中，这些边不形成循环并且具有最小的权重，直到未添加五个边，因为有六个顶点。

边       权重       添加或未添加
(B, E)           2                   添加
(C, D)           3                   添加
(A, D)           4                   添加
(C, F)           4                   添加
(B, C)           5                   添加
(E, F)           5                   未添加
(A, B)           6                   未添加
(D, E)           6                   未添加
(A, F)           7                   未添加

步骤 1

步骤 2

步骤 3

步骤 4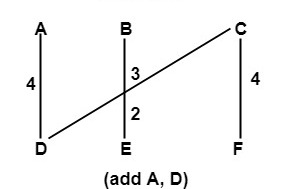

步骤 5

步骤 6： 边 (A, B)、(D, E) 和 (E, F) 被丢弃，因为它们会在图中形成循环。

因此，输出步骤 5 中形成的最小生成树，总成本为 18。

示例 2： 找出图 G 的所有生成树，并找出图中所示的 G 的最小生成树

解决方案： 图 G 共有三棵生成树，如图所示

要找到最小生成树，请使用 KRUSKAL 算法。 最小生成树如图所示

边       权重       添加或未添加
(E, F)           1                   添加
(A, B)           2                   添加
(C, D)           2                   添加
(B, C)           3                   添加
(D, E)           3                   添加
(B, D)           6                   未添加

第一个是最小生成树，具有最小权重 = 11。