离散数学中的欧拉图

如果我们想学习欧拉图，就必须了解图。图可以描述为顶点的集合，这些顶点通过一组边相互连接。我们也可以将图的研究称为图论。在本节中，我们将学习欧拉图、欧拉通路、欧拉回路、半欧拉图的定义以及欧拉图的示例。

欧拉图

如果任何连通图的所有顶点的度都是偶数，那么这种图就被称为欧拉图。换句话说，我们可以说欧拉图是一种具有欧拉回路的连通图。欧拉图的简单示例如下：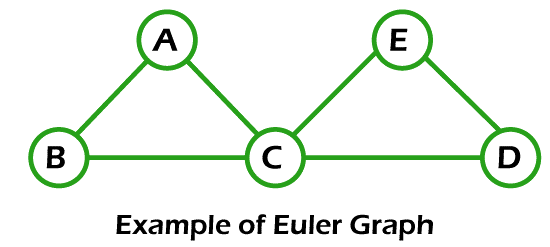

上述图是一个连通图，并且该图的顶点具有偶数度。因此，我们可以说该图是欧拉图。

换句话说，我们可以说该图是欧拉图，因为它具有欧拉回路 BACEDCB。

欧拉通路

我们也可以将欧拉通路称为欧拉行走或欧拉迹。欧拉迹和欧拉行走的定义如下：

• 如果存在一个连通图，其中有一条经过图中所有边的迹，那么这种迹就被称为欧拉迹。
• 如果存在一个连通图，它有一个经过图中每一条边一次的行走，那么这种行走就被称为欧拉行走。

注意：如果图中有超过两个顶点的度为奇数，那么这种图就被称为欧拉通路图。

欧拉通路示例

欧拉通路有很多例子，其中一些如下所示：

示例 1：在下图，我们有一个有 4 个节点的图。现在我们需要确定这个图是否包含欧拉通路。

解决方案

如果上图的每条边都恰好访问一次，并且其顶点可以重复，那么上图将包含欧拉通路。所以，如果我们从顶点 B 开始，然后去顶点 C、D、B、A 和 D，那么在这个过程中，每一条边都恰好访问了一次，并且还包含重复的顶点。所以上图包含欧拉通路，如下所示：

示例 2：在下图，我们有一个有 6 个节点的图。现在我们需要确定这个图是否包含欧拉通路。

解决方案

如果上图的每条边都恰好访问一次，并且其顶点可以重复，那么上图将包含欧拉通路。所以，如果我们从顶点 B 开始，然后去顶点 C、D、F、B、E、D、A 和 B，那么在这个过程中，每一条边都恰好访问了一次，并且还包含重复的顶点。所以上图包含欧拉通路，如下所示：

示例 3：在下图，我们有一个有 5 个节点的图。现在我们需要确定这个图是否包含欧拉通路。

解决方案

如果上图的每条边都恰好访问一次，并且其顶点可以重复，那么上图将包含欧拉通路。所以，如果我们从 A 开始，那么我们只能去顶点 A、C、D 或 B、C、E。这意味着这个图无法一次性访问所有边。所以上图不包含欧拉通路。

欧拉回路

我们也可以将欧拉回路称为欧拉环游或欧拉圈。欧拉回路有各种定义，如下所示：

• 如果存在一个连通图，其中有一条包含图中所有边的回路，那么这种回路就被称为欧拉回路。
• 如果存在一个连通图，它有一个经过图中每一条边一次的行走，那么这种行走就被称为欧拉回路。在这个行走中，起点和终点必须相同，并且这个行走可以包含重复的顶点，但不是必须的。
• 如果一个欧拉迹的起点和终点是同一个顶点，那么这种迹就被称为欧拉回路。
• 闭合的欧拉迹被称为欧拉回路。

注意：如果图的所有顶点的度都是偶数，那么这种图就被称为欧拉回路。

欧拉回路示例

欧拉回路有很多例子，其中一些如下所示：

示例 1：在下图，我们有一个有 4 个节点的图。现在我们需要确定这个图是否包含欧拉回路。

解决方案

如果上图的起点和终点相同，并且该图恰好访问每一条边一次，那么上图将包含欧拉回路。欧拉回路可以包含重复的顶点。如果我们从顶点 A 开始，然后去顶点 B、C、D 和 A，那么在这个过程中，起点和终点相同的条件得到了满足，但覆盖所有边的另一个条件没有得到满足，因为从顶点 D 到 B 有一条边没有被覆盖。如果我们尝试覆盖这条边，那么边就会重复。所以上图不包含欧拉回路。

示例 2：在下图，我们有一个有 6 个节点的图。现在我们需要确定这个图是否包含欧拉回路。

解决方案

如果上图的起点和终点相同，并且该图恰好访问每一条边一次，那么上图将包含欧拉回路。欧拉回路可以包含重复的顶点。所以，如果我们从顶点 A 开始，然后去顶点 B、C、D、F、B、E、D，然后回到 A，那么在这个过程中，起点和终点是相同的。路径（A、B、C、D、F、B、E、D、A）也恰好访问了所有边一次，并且除了起点外，不包含任何重复的顶点。所以上图包含欧拉回路，如下所示：

示例 3：在下图，我们有一个有 5 个节点的图。现在我们需要确定这个图是否包含欧拉回路。

解决方案

如果上图的起点和终点相同，并且该图恰好访问每一条边一次，那么上图将包含欧拉回路。欧拉回路可以包含重复的顶点。如果我们从顶点 A 开始，然后去顶点 C、D 或 C、E，那么在这个过程中，起点和终点相同的条件没有得到满足，但覆盖所有边的另一个条件也没有得到满足。这是因为如果我们沿着路径（A、C、D 或 A、C、E），在这个过程中许多边会重复，这违反了欧拉回路的定义。所以，如果我们尝试覆盖所有边和顶点，边就会重复。所以上图不包含欧拉回路。

半欧拉图

如果存在一个连通图，它不包含欧拉回路，但它有一个欧拉迹，那么这种图就被称为半欧拉图。任何图被称为半欧拉图，如果它满足两个条件，如下所示：

• 为此，图必须是连通的
• 该图必须包含欧拉迹

半欧拉图示例

在这个例子中，我们有一个有 4 个节点的图。现在我们需要确定这个图是否是半欧拉图。

解决方案

此处，

• 该图有一个欧拉迹，即 BCDBAD。
• 但没有欧拉回路。
• 因此，该图是半欧拉图。

重要说明

当我们学习欧拉图的概念时，有一些要点需要牢记，如下所示：

注意 1

我们有两种方法可以检查任何图是否是欧拉图。我们可以使用任何一种方法来完成，如下所示：

• 如果一个连通图包含欧拉回路，那么这种图就是欧拉图。
• 如果图中所有顶点的度都是偶数，那么这种图就是欧拉图。

注意 2

我们可以使用以下方法来检查任何图是否具有欧拉回路：

• 我们将检查图的所有顶点的度是否为偶数。
• 如果它具有偶数度，那么这种图就是欧拉回路。否则，它将不是欧拉回路。

注意 3

我们可以使用以下方法来检查任何图是否是半欧拉图：

• 我们将检查是否存在一个连通图，它有一个欧拉回路。
• 如果它是一个连通图并且有一个欧拉回路，那么这种图就是半欧拉图。否则，它将不是半欧拉图。

注意 4

我们可以使用以下方法来检查任何图是否具有欧拉迹：

• 我们将检查图中是否有超过两个顶点的度为奇数。
• 如果超过两个顶点的度为奇数，那么这种图就是欧拉迹。否则，它将不是欧拉迹。

注意 5

• 如果一个连通图包含欧拉回路，那么该图也包含欧拉迹。
• 如果一个连通图包含欧拉迹，那么该图可能包含也可能不包含欧拉回路。

注意 6

• 如果一个图是欧拉图，那么该图肯定是一个半欧拉图。
• 但半欧拉图一定是欧拉图，这是强制性的。

欧拉图示例

欧拉图有很多例子，其中一些如下所示：

示例 1：在下图，我们有 6 个节点。现在我们需要确定这个图是否是欧拉图。

解决方案

如果上图包含欧拉回路，那么它就是欧拉图。如果起点和终点相同，并且该图恰好访问每一条边一次，那么一个图就包含欧拉回路。所以，当我们从顶点 A 开始，然后去顶点 E、D、F、B、C、D，然后回到 A，那么在这个过程中，起点和终点是相同的。这条路径恰好访问了所有边一次，并且包含重复的顶点。所以该图包含欧拉回路。因此，它是欧拉图。

示例 2：在下图，我们有 5 个节点。现在我们需要确定这个图是否是欧拉图。

解决方案

如果上图包含欧拉回路，那么它就是欧拉图。如果起点和终点相同，并且该图恰好访问每一条边一次，那么一个图就包含欧拉回路。所以，如果我们从顶点 A 开始，然后去顶点 B、D 或 A、B、E，那么在这个过程中，起点和终点相同的条件得到了满足，但恰好访问所有边一次的另一个条件没有得到满足。所以，当我们沿着路径（A、B、D 或 A、B、E）行进时，在这个过程中许多边会重复，这违反了欧拉回路的定义。所以该图不包含欧拉回路。因此，它不是欧拉图。

示例 3：在下图，我们有 8 个节点。现在我们需要确定这个图是否是欧拉图。

解决方案

如果上图包含欧拉回路，那么它就是欧拉图。如果起点和终点相同，并且该图恰好访问每一条边一次，那么一个图就包含欧拉回路。所以，如果我们从顶点 A 开始，然后去顶点 D、H、E、F、G、C、B，然后回到 A，那么在这个过程中，起点和终点相同的条件得到了满足，但恰好访问所有边一次的另一个条件没有得到满足。所以，当我们沿着路径（A、D、H、E、F、G、C、B、A）行进时，在这个过程中，许多边没有被覆盖，即 A 到 E、G 到 H、F 到 B 和 D 到 C，这违反了欧拉回路的定义。所以该图不包含欧拉回路。因此，它不是欧拉图。

示例 4：在下图，我们有 7 个节点。现在我们需要确定这个图是否是欧拉图。

解决方案

如果上图包含欧拉回路，那么它就是欧拉图。所以，如果我们从顶点 A 开始，然后去顶点 F、E、G、C、D、B，然后回到 A，那么在这个过程中，起点和终点相同的条件得到了满足，但恰好访问所有边一次的另一个条件没有得到满足。这是因为欧拉回路不能重复边。所以，当我们沿着路径（A、F、E、G、C、D、B、A）行进时，在这个过程中，许多边没有被覆盖，即 F 到 G、A 到 E、E 到 D 和 B 到 C，这违反了欧拉回路的定义。所以该图不包含欧拉回路。因此，它不是欧拉图。

示例 5：在下图，我们有 5 个节点。现在我们需要确定这个图是否是欧拉图。

解决方案

如果上图包含欧拉回路，那么它就是欧拉图。所以，当我们从顶点 A 开始，然后去顶点 B、C、D、B、E，然后回到 A，那么在这个过程中，起点和终点是相同的。这条路径恰好访问了所有边一次，并且包含重复的顶点。所以该图包含欧拉回路。因此，它是欧拉图。

示例 6：在下图，我们有 9 个节点。现在我们需要确定这个图是否是欧拉图。

解决方案

如果上图包含欧拉回路，那么它就是欧拉图。所以，如果我们从顶点 A 开始，然后去顶点 B、C、D、E、F、G、H、I，然后回到 A，那么在这个过程中，起点和终点相同的条件得到了满足，但恰好访问所有边一次的另一个条件没有得到满足。所以，当我们沿着路径（A、B、C、D、E、F、G、H、I、A）行进时，在这个过程中，有一条边没有被覆盖，即 A 到 F，这违反了欧拉回路的定义。所以该图不包含欧拉回路。因此，它不是欧拉图。