离散数学中的线性相关

线性相关可以描述为衡量两个随机变量之间依赖关系的一种方法。

线性相关有各种特征，如下所述：

• 线性相关的范围在 -1 到 1 之间。
• 线性相关与协方差成正比。
• 协方差和线性相关的解释非常相似。

线性相关定义

假设有两个随机变量 X 和 Y。线性相关系数也称为皮尔逊相关系数。我们可以按照以下方式定义变量 X 和 Y 之间的线性相关系数：

其中

Cov[X, Y] 用于表示 X 和 Y 之间的协方差。

stdev[X] stdev[Y] 用于表示 X 和 Y 的标准差。

只有当存在 Cov[X, Y]、stdev[X] 和 stdev[Y] 时，我们才能定义线性相关系数。我们通常将其表示为 。

零标准差

如果 stdev[X] 和 stdev[Y] 这两个标准差都严格大于零，那么该比率才有意义。

如果两个标准差中有一个为 0，那么我们通常可以假设 Corr[X, Y] = 0。

当两个标准差中有一个为 0 时，上述假设也等同于假设 0/0 = 0，因为 Cov[X, Y] = 0。

解释

线性相关和协方差的解释非常相似。通过 X 和 Y 之间的相关性，我们可以看到它们推导之间的相似之处。-1 到 1 之间的线性相关范围描述如下：

通过相关性，我们可以轻松了解两个随机变量之间线性依赖的强度，如下所示：

• 当相关性接近 1 时，变量 X 和 Y 之间的正线性依赖关系会更强。
• 当相关性接近 -1 时，变量 X 和 Y 之间的负线性依赖关系会更强。

术语

在线性相关中，有一些术语经常使用。这些术语描述如下：

1. 如果 Corr[X, Y] > 0，则称变量 X 和 Y 为正线性相关。我们可以简单地称之为正相关。
2. 如果 Corr[X, Y] < 0，则称变量 X 和 Y 为负线性相关。我们可以简单地称之为负相关。
3. 如果 Corr[X, Y] ≠ 0，则称变量 X 和 Y 为线性相关。我们可以简单地称之为相关。
4. 如果 Corr[X, Y] = 0，则称变量 X 和 Y 为不相关。我们还可以注意到，Cov[X, Y] = 0 ? Corr[X, Y] = 0。如果 Cov[X, Y] = 0，则称两个随机变量 X 和 Y 为不相关。

示例：在此示例中，我们将有两个离散随机变量，并尝试找出它们之间的线性相关系数。

解决方案：假设有一个二维随机向量 X，我们将其条目表示为 X1 和 X2。

现在我们还将假设 X 的支撑集是：

R_X = {[-1 1], [-1 -1], [1 1]}

X 的联合概率质量函数如下所示：

X₁ 的支撑集描述如下：

R_X1 = {-1, 1}

X₁ 的概率质量函数如下所示：

X₁ 的期望值如下所示：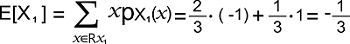

X₁² 的期望值如下所示：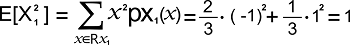

X₁ 的方差如下所示：

Var[X₁] = E[X₁²] - E[X₁]²

= 1 - (-1/3)² = 8/9

X₁ 的标准差如下所示：

现在我们将解释 X₂。

X₂ 的支撑集描述如下：

R_X2 = {-1, 1}

X₂ 的概率质量函数如下所示：

X₂ 的期望值如下所示：

X₂² 的期望值如下所示：

X₂ 的方差如下所示：

Var[X₂] = E[X₂²] - E[X₂]²

= 1 - (1/3)² = 8/9

X₂ 的标准差如下所示：

X₁X₂ 的期望值可以通过变换定理计算，如下所示：

因此，X₁ 和 X₂ 之间的协方差描述如下：

Cov[X₁, X₂] = E[X₁ X₂] - E[X₁] E[X₂] = 1/3 - (-1/3) * 1/3 = 4/9

线性相关系数描述如下：

随机变量与其自身的关联

如果存在随机变量 X，则它具有以下属性：

Corr[X, X] = 1

证明

我们可以通过以下方式证明这一点：

在证明过程中，我们使用了一个事实，该事实描述如下：

Cov[X, X] = Var[X]

对称性

线性相关系数必须是对称的，如下所示：

Corr[X, Y] = Corr[Y, X]

证明

我们可以通过以下方式证明这一点：

在证明这一点时，我们使用了协方差对称的事实，该事实描述如下：

Cov[X, Y] = Cov[Y, X]

线性相关系数的例子

线性相关系数有各种各样的例子，其中一些例子如下：

示例 1

在此示例中，我们有一个 2*1 的离散随机向量，记为 X。此向量的组成部分是 X₁ 和 X₂。

现在我们假设 X 的支撑集是：

其联合概率质量函数如下所示：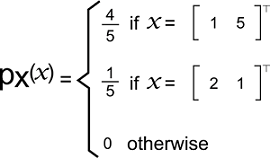

这里我们需要计算 X₁ 和 X₂ 分量之间的线性相关系数。

解决方案

X₁ 的支撑集描述如下：

R_X1 = {1, 2}

其边际概率质量函数如下所示：

X₁ 的期望值描述如下：

X₁² 的期望值描述如下：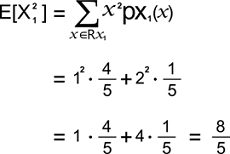

X₁ 的方差描述如下：

Var[X₁] = E[X₁²] - [X₁]²

= 8/5 - (6/5)²

= (40-36)/25

= 4/25

X₁ 的标准差描述如下：

现在我们将展示 X₂。

因此，X₂ 的支撑集描述如下：

R_x2 = {1, 5}

其边际概率质量函数如下所示：

X₂ 的期望值描述如下：

X₂² 的期望值描述如下：

X₂ 的方差描述如下：

Var[X₂] = E[X₂²] - E[X₂]²

= 101/5 - (21/5)²

= (505-441)/25

= 64/25

X₁ 的标准差描述如下：

X₁X₂ 的期望值可以通过变换定理计算，如下所示：

因此，X₁ 和 X₂ 之间的协方差描述如下：

Cov[X₁, X₂] = E[X₁ X₂] - E[X₁] E[X₂]

= 22/5 - (6/5) * 21/5

= (110-126)/25

= -16/25

X₁ 和 X₂ 之间的线性相关系数描述如下：

示例 2

在此示例中，我们有一个 2*1 的离散随机向量，记为 X。X 的条目是 X₁ 和 X₂。

现在我们假设 X 的支撑集是：

其联合概率质量函数如下所示：

这里我们需要计算 X₁ 和 X₂ 条目之间的线性相关系数。

解决方案

X₁ 的支撑集描述如下：

R_X1 = {1, 2, 3}

其边际概率质量函数如下所示：

X₁ 的均值描述如下：

X₁² 的期望值描述如下：

X₁ 的方差描述如下：

Var[X₁] = E[X₁²] - [X₁]²

= 14/3 - (2)²

= (14-12) /3

= 2/3

X₁ 的标准差描述如下：

现在我们将展示 X₂。

X₂ 的支撑集描述如下：

R_X2 = {1, 2, 3}

其概率质量函数如下所示：

X₂ 的均值描述如下：

X₂² 的期望值描述如下：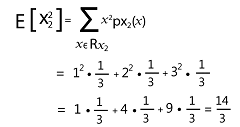

X₂ 的方差描述如下：

Var[X₂] = E[X₂²] - [X2]²

= 14/3 - (2)²

= (14-12) /3

= 2/3

X₂ 的标准差描述如下：

X₁X₂ 的期望值可以通过变换定理计算，如下所示：

因此，将这些部分组合起来，X₁ 和 X₂ 之间的协方差将变为如下：

Cov[X₁, X₂] = E[X₁ X₂] - E[X₁] E[X₂]

= 13/3 - 2 * 2

= (13-12) /3

= 1/3

X₁ 和 X₂ 之间的线性相关系数描述如下：

示例 3

在此示例中，我们有一个连续随机向量 [X, Y]，我们假设该向量的支撑集是：

R_XY = [0, ∞) * [1, 2]

其联合概率密度函数如下所示：

这里我们需要计算 X 和 Y 之间的线性相关系数。

解决方案

Y 的支撑集描述如下：

R_Y = [1, 2]

当 y ∉ R_Y 时，Y 的边际概率密度函数为零。我们可以通过将联合概率密度中的 x 积分出来来获得 Y 的边际概率密度函数，如下所示：

因此，我们可以得到 Y 的边际概率密度函数如下：

Y 的期望值描述如下：

Y² 的期望值描述如下：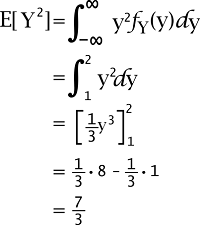

Y 的方差描述如下：

Var[Y] = E[Y²] - E[Y]²

= 7/3 - (3/2)²

= (28-27) /12

= 1/12

Y 的标准差描述如下：

现在我们将展示 X。

X 的支撑集描述如下：

Rx = [0, ∞)

当 x ∉ R_X 时，X 的边际概率密度函数为零。我们可以通过将联合概率密度中的 y 积分出来来获得 X 的边际概率密度函数，如下所示：

在这种情况下，对于密度函数，积分不能明确计算，但我们可以使用以下方法来表示 X 的边际概率密度函数：

X 的期望值描述如下：

X² 的期望值描述如下：

X 的方差描述如下：

Var[X] = E[X²] - E[X]²

= 1/4 - (1/2 In(2))²

= ¼ [1 - (In(2))²]

= 1/12

X 的标准差描述如下：

XY 的期望值可以通过变换定理计算，如下所示：

因此，将这些部分组合起来，X 和 Y 之间的协方差将变为如下：

Cov[X, Y] = E[XY] - E[X] E[Y]

= 1/2 - 1/2 In(2) * 3/2

= 1/2 - 3/4 In(2)

X 和 Y 之间的线性相关系数描述如下：