平面图

如果一个图可以在平面上绘制，并且没有任何边交叉，则称该图为平面图。

示例： 图中所示的图是平面图。

图的区域： 考虑一个平面图 G=(V,E)。区域被定义为由边界定的平面区域，并且不能进一步细分。平面图将平面划分为一个或多个区域。其中一个区域将是无限的。

有限区域： 如果区域的面积是有限的，则该区域称为有限区域。

无限区域： 如果区域的面积是无限的，则该区域称为无限区域。平面图只有一个无限区域。

示例： 考虑图中所示的图。确定区域、有限区域和无限区域的数量。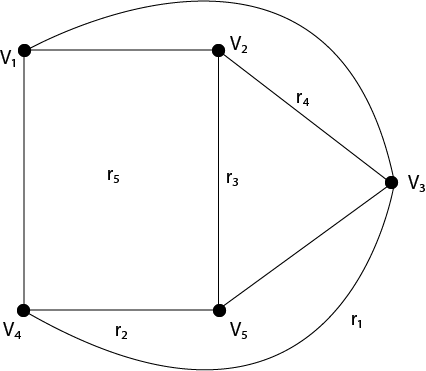

解答： 上图中共有五个区域，即 r₁,r₂,r₃,r₄,r₅。

图中共有四个有限区域，即 r₂,r₃,r₄,r₅。

只有一个无限区域，即 r₁

平面图的性质

1. 如果一个连通平面图 G 有 e 条边和 r 个区域，则 r ≤e。
2. 如果一个连通平面图 G 有 e 条边、v 个顶点和 r 个区域，则 v-e+r=2。
3. 如果一个连通平面图 G 有 e 条边和 v 个顶点，则 3v-e≥6。
4. 完全图 K_n 是平面图当且仅当 n<5。
5. 完全二分图 K_mn 是平面图当且仅当 m<3 或 n>3。

示例： 证明完全图 K₄ 是平面图。

解答： 完全图 K₄ 包含 4 个顶点和 6 条边。

我们知道，对于连通平面图，3v-e≥6。因此，对于 K₄，我们有 3x4-6=6，它满足性质 (3)。

因此 K₄ 是一个平面图。证明完毕。

非平面图

如果一个图不能在平面上绘制而没有任何边交叉，则称该图为非平面图。

示例： 图中所示的图是非平面图。

这些图不能在平面上绘制而没有任何边交叉，因此它们是非平面图。

非平面图的性质

一个图是非平面图当且仅当它包含一个同胚于 K₅ 或 K_3,3 的子图。

示例 1： 证明 K₅ 是非平面图。

解答： 完全图 K₅ 包含 5 个顶点和 10 条边。

现在，对于连通平面图，3v-e≥6。

因此，对于 K₅，我们有 3 x 5-10=5（不满足性质 3，因为它必须大于或等于 6）。

因此，K₅ 是一个非平面图。

示例 2： 通过找到一个同胚于 K₅ 或 K_3,3 的子图，证明图中所示的图是非平面图。

解答： 如果我们移除边 (V₁,V₄),(V₃,V₄) 和 (V₅,V₄)，则图 G₁ 与 K₅ 同胚。因此它是非平面图。

如果我们移除边 V_2,V7)，则图 G₂ 与 K_3,3 同胚。因此它是非平面图。

图着色

假设 G=(V,E) 是一个没有重边的图。图 G 的顶点着色是将颜色分配给 G 的顶点，使得相邻顶点具有不同的颜色。如果存在使用 M 种颜色的着色，则图 G 是 M-可着色的。

proper coloring (正确着色)： 如果任意两个相邻顶点 u 和 v 具有不同的颜色，则该着色是正确的，否则称为不正确着色。

示例： 考虑以下图，并使用颜色 C={r, w, b, y}。使用所有颜色或更少的颜色正确地为图着色。

图中所示的图是最小 3-可着色的，因此 x(G)=3

解答： 图中显示了使用所有四种颜色正确着色的图。

图中显示了使用三种颜色正确着色的图。

G 的色数： 产生图 G 的正确着色所需的最小颜色数称为 G 的色数，记为 x(G)。

示例： K_n 的色数是 n。

解答： K_n 的着色可以通过为每个顶点分配不同的颜色来构建，使用 n 种颜色。由于该图中的任意两个顶点都相邻，因此不能为两个顶点分配相同的颜色。因此，K_n 的色数=n。

图着色的应用

图着色的一些应用包括

• 寄存器分配
• 地图着色
• 二分图检查
• 移动无线电频率分配
• 制定时间表等。

陈述并证明握手定理。

握手定理： 图 G 中所有顶点的度数之和等于图中边数的两倍。

数学上可以表述为

              ∑_v∈Vdeg(v)=2e

证明： 令 G = (V, E) 为一个图，其中 V = {v₁,v₂, . . . . . . . . . .} 为顶点集，E = {e₁,e₂ . . . . . . . . . .} 为边集。我们知道每条边连接两个顶点，因此它为每个顶点贡献一度。因此，每条边为图贡献一度。所以，所有顶点的度数之和等于 G 中边数的两倍。

因此，        ∑_v∈Vdeg(v)=2e