离散数学中的图度量

在本节中，我们将首先学习图，以了解图的测量。之后，我们将学习图的测量，包括图的长度、两个顶点之间的距离、图的直径、图的半径、图的中心、图的偏心距、图的周长和图的基数。

Graph

图可以被描述为顶点和边的集合，其中顶点可以被描述为点的集合，边可以被描述为连接这些点的线。这里V用于表示顶点，E用于表示边。图包含许多性质，并且基于图的结构，我们可以表征图。在本节中，我们将学习一些图的基本性质，这些性质在所有类型的图中都很常见。

例如

在上图中，我们有一组顶点和边，如下所示：

顶点 = {1, 2, 3, 4, 5, 6}

边 = {{1, 2}, {1, 4}, {1, 5}, {2, 3}, {3, 5}, {3, 6}, {4, 5}, {5, 6}}

图测量

我们可以通过一些性质来测量任何图，如下所述：

1. 图的长度
2. 两个顶点之间的距离
3. 图的偏心距
4. 图的直径
5. 图的半径
6. 图的中心
7. 图的周长
8. 图的基数

现在我们将逐一学习它们，如下所示：

图的长度

我们可以通过计算图中包含的边的数量来确定图的长度。计算图长度的示例如下：

在上图中，长度为 8，即：

12, 23, 34, 45, 56, 61, 13, 35

两个顶点之间的距离

我们可以通过计算最短或最小路径中的边数来确定两个顶点之间的距离。它用于提供两个边之间的最小距离。一个图可以有两个顶点之间有多条最短路径。所以，如果两个顶点通过多条路径连接，在这种情况下，最短路径将被假定为两个顶点之间的距离。

符号 - d(U, V)

一个图可以包含从一个顶点到另一个顶点的多条路径。要确定这两个顶点之间的距离，我们必须只选择这两条顶点之间的最短路径。

示例

计算两个顶点之间距离的示例如下：

上图显示顶点 4 到顶点 5 的距离为 1。这是因为这两个顶点之间只有一条边。还有一些其他路径可以从顶点 4 到达顶点 5，如下所示：

1. 41, 12, 25
2. 46, 67, 75
3. 45（此路径将用于计算两个顶点之间的距离）
4. 45, 53, 31, 12, 25
5. 41, 13, 36, 67, 75

因此，两个顶点之间的距离是 1。

这是另一个关于两个顶点之间距离的例子，如下图所示：

上图显示顶点 1 到顶点 5 的距离为 2。这是因为这两个顶点之间有两条边。还有一些其他路径可以从顶点 1 到达顶点 5，如下所示：

1. 1, 0, 4, 5
2. 1, 2, 5（此路径将用于计算两个顶点之间的距离）
3. 1, 0, 2, 5

因此，从 1 到 5 的距离是 2。

图的偏心距

我们可以通过计算一个顶点到另一个顶点的最大距离来确定偏心距。因此，顶点的偏心距将是该顶点到所有其他顶点的最大距离。符号 e(V) 用于表示图的偏心距。

符号 - e(V)

我们将首先计算特定顶点到所有其他顶点的距离，然后找出所有距离中的最大值。这个最大距离将是图的偏心距。

示例

确定图的偏心距的示例如下：

在这里，顶点 1 的偏心距是 3。

顶点 1 到顶点 2 的距离是 1（'12'）。

顶点 1 到顶点 3 的距离是 1（'13'）。

顶点 1 到顶点 4 的距离是 1（'14'）。

顶点 1 到顶点 5 的距离是 2（'12'-'25'）或（'14'-'45'）。

顶点 1 到顶点 6 的距离是 2（'13'-'36'）或（'14'-'46'）。

顶点 1 到顶点 7 的距离是 3（'13'-'36'-'67'）或（'14'-'46'-'67'）。

所以，总之，偏心距将是 3，因为我们看到顶点 1 到顶点 7 的最大距离是 3，这是最大距离。

换句话说，偏心距可以表示为：

e(2) = 3

e(3) = 3

e(4) = 2

e(5) = 3

e(6) = 3

e(7) = 3

因此，图 G 的偏心距是 3。

这是另一个关于图的偏心距的例子，如下图所示：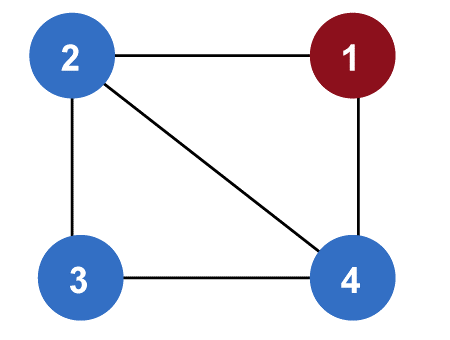

顶点 1 到顶点 1 的距离是 0（'11'）。

顶点 1 到顶点 2 的距离是 1（'12'）。

顶点 1 到顶点 3 的距离是 2（'12'-'23'）。

顶点 1 到顶点 4 的距离是 1（'14'）。

正如我们所见，上述距离的最大值为 2。

因此，图 G 的偏心距是 2。

图的直径

我们可以通过计算顶点对之间的最大距离来确定图的直径。我们将通过确定所有路径来解决它，然后确定所有路径之间的最大值。换句话说，图的直径可以通过确定所有顶点的最大偏心距来计算。

符号 -d(G)

在图中，我们将首先检查所有顶点的偏心距，然后检查所有偏心距中的最大值。这个最大偏心距将是图的直径。

示例

计算图直径的示例如下：

在上图中，直径是 3。原因如下面的图的偏心距所示：

e(2) = 3

e(3) = 3

e(4) = 2

e(5) = 3

e(6) = 3

e(7) = 3

我们可以看到最大偏心距是 3，即 d(G) = 3。

因此，图 G 的直径是 3。

这是另一个关于图的直径的例子，如下图所示：

在上图中，半径是 3。这是因为此图的最大偏心距是 3，如下所示：

23, 36, 67

因此，图 G 的直径是 3。

图的半径

只有当一个图有直径时，我们才能计算该图的半径。图的半径可以描述为从特定顶点到所有其他顶点的所有最大距离中的最小值。符号 r(G) 用于表示图的半径。换句话说，图的半径可以通过确定所有顶点的最小偏心距来计算。

符号 - r(G)

在图中，我们将首先检查所有顶点的偏心距，然后检查所有偏心距中的最小值。这个最小偏心距将是图的半径。

示例

计算图半径的示例如下：

在上图中，半径是 2。原因如下面的图的偏心距所示：

e(2) = 3

e(3) = 3

e(4) = 2

e(5) = 3

e(6) = 3

e(7) = 3

我们可以看到顶点 4 的最小偏心距是 2。

因此，图 G 的半径是 2。

这是另一个关于图的半径的例子，如下图所示：

在上图中，半径是 2。原因是可以通过查看所有可用的最小半径得出，如下所述：

BC, CF

BC, CE

BC, CD

BC, CA

因此，图 G 的半径是 2。

图的中心

如果一个图的所有顶点都具有最小偏心距，那么我们可以计算该图的中心。图的中心可以由 G 的所有中心点的集合来描述。在这里，半径和偏心距是相似的。如果 e(V) = r(V)，则顶点 V 被称为图 G 的中心点。

例如： 如果村庄中心有一个学校，那么公交车就不需要 travel 太多，因为它会减少距离。确定图的中心的示例如下：

在上图中，中心点是顶点 4。这是因为：

e(4)= r(4) = 2

这是另一个关于图的中心的例子，如下图所示：

在上图中，中心点是 A。

图的周长

我们可以通过计算图中longest cycle的边数来确定图的周长。确定图的周长的示例如下：

在上图中，周长是 6。这是因为，从上图，我们可以得到两个 longest cycles，即 1-2-6-7-5-2-1 或 1-2-6-4-5-2-1，并且 longest cycle 有 6 条边。所以这个图的周长将是 6。

图的基数

我们可以通过计算图中shortest path的边数来确定图的基数。确定图的基数的示例如下：

在上图中，基数是 4。这是因为，从上图，我们可以得到三个 shortest cycles，即 1-3-6-4-1 或 4-6-7-5-4-1 或 1-2-5-4-1，并且 shortest cycle 有 4 条边。所以这个图的基数将是 4。