离散数学中的反厄米矩阵

斜对称矩阵和斜埃尔米特矩阵有很多相似之处。对于斜对称矩阵，给定矩阵的负数和矩阵的转置是相似的。同样，对于斜埃尔米特矩阵，给定矩阵的负数和矩阵的共轭转置是相似的。我们也可以称斜埃尔米特矩阵为反埃尔米特矩阵。在本节中，我们将学习斜埃尔米特矩阵、其公式、性质、示例、将矩阵分解为埃尔米特矩阵和斜埃尔米特矩阵等等。

什么是斜埃尔米特矩阵

如果一个方阵满足矩阵的负数与其共轭转置矩阵相似，则该矩阵称为斜埃尔米特矩阵，即 A^H = -A。其中 A^H 用来表示矩阵 A 的共轭转置。它也可以用符号 A∗ 来表示。现在我们将学习 A^H 以更好地理解斜埃尔米特矩阵的概念。通过将 A 的转置 (即 A^T) 的每个元素替换为其复共轭，我们可以得到矩阵 A 的共轭转置。如果有一个复数 x + iy，则该复数的复共轭将是 x - iy。现在我们将通过一个示例来学习，该示例描述如下。

示例： 在此示例中，我们有一个矩阵 A，并且需要说明该矩阵如何成为斜埃尔米特矩阵。矩阵 A 的元素描述如下。

解： 矩阵 A 的转置描述如下。

现在我们将按以下方式计算矩阵 A 的共轭转置。

现在我们将按以下方式计算矩阵 A 的负数。

从方程 1 和方程 2 中，我们可以看到：

A^H = -A

因此，矩阵 A 是一个斜埃尔米特矩阵。

设 A 是一个斜埃尔米特矩阵，A 和 A^H 分别包含元素 xij 和 x̅ij。如果这些元素位于第 i 行和第 j 列的位置，在这种情况下，xij = -x̅ji。这个陈述表明，一个方阵 A 当且仅当它满足以下条件时才是一个斜埃尔米特矩阵。

A^H = -A 或者

xij = -x̅ji

斜埃尔米特矩阵的公式

关于任意阶数的斜埃尔米特矩阵，有一些有趣的结论。这些结论描述如下。

• 斜对称矩阵的对角线值将是纯虚数或零。
• 斜埃尔米特矩阵的对角线元素以外的所有元素可能包含实部和虚部。
• 如果该矩阵（对角线元素除外）的第 i 行和第 j 列包含虚部，在这种情况下，两个位置将相同。
• 如果该矩阵（对角线元素除外）的第 i 行和第 j 列包含实部，在这种情况下，两个位置将相同，但符号不同。

上述斜埃尔米特矩阵示例的对角线元素是纯虚数（或为零）。在上面的示例中，我们还可以看到 a12 = 1+i 且 a21 = -1+i。基于这些，我们可以构建一个 2x2 的斜埃尔米特矩阵的公式。因此，我们可以以下形式展示 2x2 的斜埃尔米特矩阵。

其中 x、y、z 和 w 用于表示实数。

类似地，我们也可以构建一个 3x3 的斜埃尔米特矩阵的公式。因此，我们可以以下形式展示 3x3 的斜埃尔米特矩阵。

斜埃尔米特矩阵的性质

斜埃尔米特矩阵有各种性质，其中一些描述如下。

• 如果有一个斜对称矩阵且该矩阵的元素是实数，则此类型的矩阵将始终是斜埃尔米特矩阵。
• 对于斜埃尔米特矩阵，对角线元素将始终包含虚数或零。
• 该矩阵将是可对角化的。
• 对于斜埃尔米特矩阵，特征值将是零或纯虚数。
• 如果有一个斜埃尔米特矩阵 A，则当且仅当 n 为奇数时，Aⁿ 也是斜埃尔米特矩阵。当且仅当 n 为偶数时，Aⁿ 将是埃尔米特矩阵。
• 如果我们对两个斜埃尔米特矩阵进行加法或减法，则结果矩阵将是斜埃尔米特矩阵。
• 如果我们对两个埃尔米特矩阵进行乘法，则结果矩阵将是埃尔米特矩阵。
• 如果我们乘以一个标量值和一个斜埃尔米特矩阵，则结果矩阵必须是斜埃尔米特矩阵。
• 如果有一个斜埃尔米特矩阵 A，则 iA 将是埃尔米特矩阵。

将矩阵分解为埃尔米特矩阵和斜埃尔米特矩阵

如果有一个方阵，我们可以将其写成一个埃尔米特矩阵 X 和一个斜埃尔米特矩阵 Y 的和。

假设有一个方阵 A。则，

A = X + Y

A = (1/2) (A + A^H) + (1/2) (A - A^H)。其中 A^H 用于表示矩阵 A 的共轭转置。

其中

X = (1/2) (A + A^H) 且

Y = (1/2) (A - A^H)

这表明：

• 如果埃尔米特矩阵用 A + A^H 表示，那么 (1/2) × (A + A^H) 也将表示埃尔米特矩阵。
• 如果斜埃尔米特矩阵用 A - A^H 表示，那么 (1/2) × (A - A^H) 也将表示斜埃尔米特矩阵。

因此，如果有一个方阵，我们可以将其写成斜埃尔米特矩阵和埃尔米特矩阵的和。

要点

并非所有正规矩阵都是斜埃尔米特矩阵。在学习斜埃尔米特矩阵的概念时，有一些重要的点我们应该知道。这些点描述如下。

• 如果我们对斜埃尔米特矩阵进行共轭运算，则结果总是会得到一个斜埃尔米特矩阵。
• 如果我们对斜埃尔米特矩阵进行转置运算，则结果总是会得到一个斜埃尔米特矩阵。
• 如果我们计算斜埃尔米特矩阵的迹，则它将是虚数或零。
• 如果有一个方阵 A，则 A - A∗ 是一个斜埃尔米特矩阵。
• 如果我们计算一个奇数阶斜埃尔米特矩阵的行列式，则行列式的结果将为零。

斜埃尔米特矩阵的示例

斜埃尔米特矩阵有很多示例，其中一些描述如下。

示例 1： 在此示例中，我们有一个矩阵 A，并且需要确定它是否为斜埃尔米特矩阵。矩阵 A 的元素描述如下。

解： 首先，我们将计算给定矩阵 A 的转置，如下所示。

现在我们将计算上述转置矩阵的共轭，如下所示。

现在我们将计算给定矩阵 A 的负数，如下所示。

从方程 1 和方程 2 中，我们可以看到：

A^H = -A

因此，给定的矩阵是斜埃尔米特矩阵。

答案：矩阵 A 是斜埃尔米特矩阵。

示例 2： 在此示例中，我们有两个斜埃尔米特矩阵，需要确定这两个矩阵的加法。还需要证明此加法的结果也是斜埃尔米特矩阵。这两个斜埃尔米特矩阵的元素描述如下。

解： 根据题目，我们有两个斜埃尔米特矩阵 A 和 B。这两个矩阵的加法描述如下。

现在我们将计算此加法的转置，如下所示。

现在我们将计算 A+B 的共轭转置，如下所示。

现在我们将计算 A+B 的负数，如下所示。

从方程 1 和方程 2 中，我们可以看到：

(A+B)^H = - (A+B)

答案：两个斜埃尔米特矩阵的加法将是一个斜埃尔米特矩阵。

示例 3： 在此示例中，我们有一个矩阵 A，需要将其分解为埃尔米特矩阵和斜埃尔米特矩阵的和。矩阵 A 的元素描述如下。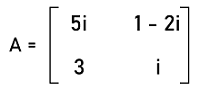

解： 根据题目，我们有一个矩阵 A，其中

该矩阵的复共轭描述如下。

正如我们所学，A = X+Y，其中

X 用于表示埃尔米特矩阵，其中 X = (1/2) (A + A^H)

Y 用于表示斜埃尔米特矩阵，其中 Y = (1/2) (A - A^H)

现在我们将逐个将 A 和 A^H 的值代入 X 和 Y。首先，我们将考虑 X。所以

X = (1/2) (A + A^H)

现在我们将把 A 和 A^H 的值代入 Y。

Y = (1/2) (A - A^H)

答案