离散数学中的关联矩阵是什么

关联矩阵可以被描述为一种展示图的矩阵。也就是说，关联矩阵用于绘制图。我们将使用符号 [A_c] 来表示关联矩阵。与其他所有矩阵一样，此矩阵也包含行和列。

在图中，节点的数量由关联矩阵 [A_c] 的行表示，分支的数量由该矩阵的列表示。如果给定的关联矩阵有 n 行，则表示该矩阵对应的图有 n 个节点。同样，如果给定的关联矩阵有 m 列，则表示该矩阵对应的图有 m 个分支。

上面的图是一个有 6 个分支和 4 个节点的有向图。所以我们可以说这个图有 6 列和 4 行用于关联矩阵。关联矩阵的条目始终为 -1、0、+1。关联矩阵总是与 KCL（基尔霍夫电流定律）相对应。因此，可以从 KCL 推导出以下内容：

构造关联矩阵的步骤

可以通过一些步骤来绘制关联矩阵，这些步骤如下所述：

1. 如果在第 k 个节点有一个出向分支，则写入 +1。
2. 如果在第 k 个节点有一个入向分支，则写入 -1。
3. 所有其他分支都写入 0。

关联矩阵的例子

在这个例子中，我们有一个有向图，并且我们要绘制该图的关联矩阵。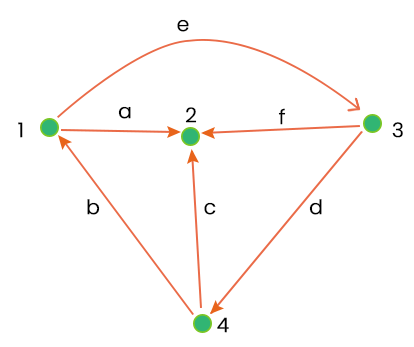

上述图的关联矩阵描述如下：

[A_C] =

约简关联矩阵

如果我们从给定的关联矩阵中删除任意一行，在这种情况下，新创建的矩阵将被称为约简关联矩阵。新创建的矩阵或约简矩阵用符号 [A] 表示。这个约简关联矩阵的阶数是 (n-1)*b，其中 b 用于表示分支的数量，n 用于表示节点的数量。上述关联矩阵的约简关联矩阵描述如下：

[A] =

在此矩阵中，我们删除了关联矩阵 [A_C] 的节点 4。

约简关联矩阵的例子

为了展示约简关联矩阵的例子，我们将考虑一个关联图。现在我们要为这个关联图写出约简关联矩阵。

解决方案

为了绘制约简关联矩阵，我们首先需要绘制给定图的关联矩阵。上述图的关联矩阵描述如下：

[A_C] =

现在我们将绘制该矩阵的约简关联矩阵，其描述如下：

[A] =

在此矩阵中，我们删除了关联矩阵 [A_C] 的节点 2。

关联矩阵的例子

示例：在此示例中，我们需要用关联矩阵表示下图所示的图。

解：上述图是一个无向图，该图的伪图描述如下：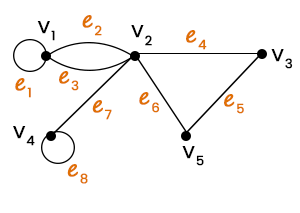

该图的关联矩阵描述如下：

借助关联矩阵，我们还可以表示多条边和自环。在关联矩阵中，列用于显示具有相同条目的多条边。这是因为这些边与相同的顶点对相关联。我们可以通过具有恰好一个等于 1 的条目的列来表示自环，该条目对应于与该自环相关联的顶点。

重要提示

在学习关联矩阵时，我们应该记住一些要点，这些要点如下所述：

• 如果我们想检查任何创建的关联矩阵的正确性，我们将检查列的总和。
• 如果列的总和为零，则创建的关联矩阵 [A_C] 是正确的。否则，关联矩阵将是不正确的。
• 我们只能使用有向图来应用关联矩阵。
• 一行中非零条目的数量告诉我们连接到该节点的边的数量。边的数量也称为该节点的度。
• (n-1) 用于表示完整关联矩阵的秩，其中 n 用于表示图的节点数。
• (n*b) 用于表示关联矩阵的阶，其中 b 用于表示图的分支数。
• 如果我们想绘制完整的关联矩阵，那么我们可以使用约简关联矩阵来完成。因此，我们将根据条件简单地添加 +1、0 或 -1，以使每列的总和为零。