离散数学中的矩阵

矩阵可以被描述为数字的矩形阵列。一个具有 m 行和 n 列的矩阵，则称为 m∗n 矩阵。如果有多个矩阵，则称为矩阵。

我们可以用大写字母来表示矩阵。数字的阵列用括号或方括号括起来。

例如

我们不能用直线代替括号来写矩阵。因为矩阵

在线性代数领域中具有特殊含义。如果我们想表示元素，我们可以使用简写符号，即 A = [a_ij]。在这个符号中，第一个下标 i 用于表示行号，下标 j 用于表示元素 a_ij 的列号。因此，如果我们想写 a₂₃，它将指第 2 行第 3 列的元素。使用这个符号，我们无法显示矩阵的维度。从这个符号，我们可以说两个 m∗n 矩阵 A = [a_ij] 和 B = [b_ij] 相等当且仅当对于所有 i 和 j，a_ij = b_ij。

例如：在此示例中，我们有一个 2∗3 矩阵。

如果一个矩阵的行数和列数**相同**，则该矩阵称为**方阵**。如果两个给定矩阵包含**相同**的行数和列数，并且它们在每个位置的**对应元素**都相同，则这些矩阵将**相等**。

例如：在此示例中，我们有一个 3∗2 矩阵，描述如下

假设有一个矩阵 A，其中

在此矩阵中，矩阵 A 的第 i 行将是 1∗n 矩阵 [a_i1, a_i2, ...., a_in]，而矩阵 A 的第 j 列将是 n∗1 矩阵，描述如下

A 的 (i, j) 元素或条目可以描述为元素 a_ij，表示 A 中第 i 行和第 j 列的数字。

有一种方便的方法可以简单地表示矩阵 A，即 A = [a_ij]。这个等式表明存在一个矩阵 A，其 (i, j) 元素等于 a_ij。

一些要点

学习矩阵时，有一些术语我们应该知道，它们描述如下

元素

矩阵中的每个值都被称为元素，无论是数字还是常数。

维度

矩阵的维度可以描述为行数乘以列数。根据维度，我们可以命名矩阵。

例如：在此示例中，我们必须确定每个矩阵的维度。

在这个矩阵中，有 3 行 2 列。所以这个矩阵的维度是 3∗2。

在这个矩阵中，有 2 行 4 列。所以这个矩阵的维度是 2∗4。

在这个矩阵中，有 4 行 1 列。所以这个矩阵的维度是 4∗1。

行矩阵

如果一个矩阵只有一行，那么它就是行矩阵。这个矩阵用 [1∗n] 表示。单行矩阵描述如下

A[a1 a2 a3, ...., an] = {aj}

列矩阵

如果一个矩阵只有一列，那么它就是列矩阵。这个矩阵用 [m∗1] 表示。单列矩阵描述如下

方阵

如果一个矩阵的行数和列数相等，那么它就是一个方阵。 (n∗n) 将是一个方阵。

例如

相等矩阵

假设有两个矩阵 A = [a_ij] 和 B = [b_ij]。这两个矩阵被称为相等矩阵 (A = B) 当且仅当 A 的每个元素都与 B 的对应元素相同，即 a_ij = b_ij 对于 1 ≤ I ≤ m，1 ≤ j ≤ n。

例如：假设有两个相等矩阵 A 和 B (A = B)，其中

现在需要确定 a, b, c, d 的值。

解答：根据题意，我们有 A = B。所以

A = 1
B = 0
C = -4
D = 2

矩阵的性质

1. (AB)^-1 = B^-1 A^-1
2. (AT)^T = A 和 (λA)^T = λA^T
3. (A + B)^T = A^T + B^T
4. (A B)^T = B^T A^T

矩阵运算

矩阵可以执行各种运算，它们描述如下

1. 矩阵加法
2. 矩阵减法
3. 矩阵相等
4. 矩阵乘法

现在我们将逐一解释它们。

矩阵加法

假设有两个矩阵 A 和 B，其中 A = [a_ij] 和 B = [b_ij]。此处 i 和 j 用于表示任何值。该矩阵的形式为 m∗n。使用符号 A+B，我们可以表示 A 和 B 的和。如果 A = a_ij 且 B = b_ij，则 A 和 B 的加法可以描述如下

A + B = aij + bij

假设有两个矩阵 A 和 B，它们包含以下元素

A 和 B 的加法将是 C，它包含以下矩阵

例如

性质

矩阵加法包含一些性质，它们描述如下

假设矩阵 A、B 和 C 是可相容的。那么

它将包含交换律，它包含以下关系

A+B = B+A

它将包含结合律，它包含以下关系

A+(B+C) = (A+B)+C

它将包含分配律，它包含以下关系

λ(A+B) = λA + λB，其中 λ 用于表示标量。

矩阵减法

在减法过程中，我们将减去给定矩阵中相同位置的元素。如果存在两个具有相同维度或相同阶数的矩阵 A 和 B，我们才能减去它们。如果两个给定矩阵具有两个不同的阶数，则我们不能对它们执行减法运算。使用符号 A-B，我们可以表示 A 和 B 的减法。如果 A = a_ij 且 B = b_ij，则 A 和 B 的减法可以描述如下

A - B = aij - bij

此处 i 和 j 可以是任何值。

示例 1

示例 2：假设有两个矩阵 A 和 B。现在需要计算两个给定矩阵的和与差。矩阵 A 和矩阵 B 描述如下

解决方案

矩阵相等

假设有两个矩阵 A 和 B。这两个矩阵相等，如果矩阵中的行数和列数相同，并且 A 中每个位置的元素与 B 中对应位置的元素相同。在这种类型的矩阵中，矩阵将具有相同的对应条目。

例如

矩阵乘法

如果存在两个矩阵，A 是 m∗k 矩阵，B 是 k∗n 矩阵。我们只能在第一个矩阵的列数与第二个矩阵的行数相同时才能执行两个给定矩阵的乘法运算。使用符号 A∗B，我们可以表示 A 和 B 的乘法。在乘法过程中，我们将进行行与列的乘法。如果存在矩阵 A，它是 a∗b 矩阵，另一个矩阵 B 是 b∗c 矩阵，则 A 和 B 的乘法可以描述如下

C = AB

此处矩阵 C 用于表示结果矩阵。

假设矩阵 C 包含元素 x 和 y，则其定义为

Cxy = Ax1By1 + Ax2By2 + .... + AxbBby = ∑bk=1 AxkBky

对于 x = 1....a 和 y = 1....c

在此过程中，将矩阵 A 的第 i 行与矩阵 B 的第 j 列对应元素的乘积之和将等于 A∗B 矩阵的 (i, j) 条目。

例如：在此示例中，我们有两个矩阵，描述如下

第一个矩阵的维度是 2∗3，第二个矩阵的维度是 3∗2。因此，我们可以看到第一个矩阵的行数等于第二个矩阵的列数。同样，第一个矩阵的列数等于第二个矩阵的行数。因此，我们可以相乘给定的矩阵。

矩阵乘法示例

矩阵乘法有各种示例，其中一些描述如下

示例 1：在此示例中，我们有两个矩阵 A 和 B，其中

现在我们需要显示 AB 是否等于 BA。

解答：通过将 AB 相乘，我们将得到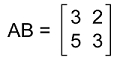

通过将 BA 相乘，我们将得到

因此，我们可以看到 AB **≠** BA。

这是因为矩阵乘法不是可交换的。

示例 2：在此示例中，我们有三个矩阵 A、B 和 C，其中

现在需要确定 A(B+C) 和 AB+AC。

解答：首先，我们将像这样求解 A(B+C)

现在我们将像这样求解 AB+AC

示例 3：在此示例中，我们有两个矩阵，并且需要确定 C = AB。矩阵 A 和 B 显示如下

解决方案

矩阵乘法性质

矩阵乘法包含一些性质，它们描述如下

假设矩阵 A、B 和 C 是可相容的。那么

A(B+C)= AB + AC
(A+B)C = AC + BC
A(BC) = (AB)C

单位矩阵

单位矩阵可以描述为其中给定矩阵的所有对角线元素都为 1 的矩阵。单位矩阵用符号 I 表示。

例如

A∗I = A

n 阶单位矩阵可以描述为 n∗n 矩阵 I_n = [ð_ij]，其中 ð_ij= 1 当 i = j 时，ð_ij = 0 当 i ≠ j 时。因此

Ar = A ∗ A ∗ A ... ∗ A (r times)
A0 = In

单位矩阵示例

这是一个 2∗2 单位矩阵，因为该矩阵的对角线元素为 1。

这是一个 3∗3 单位矩阵，因为该矩阵的对角线元素也为 1。

矩阵的转置

假设有一个矩阵 A = [a_ij]，它是一个 m∗n 矩阵。我们可以通过交换 A 的行和列来得到矩阵 A 的转置。使用符号 A' 或 A^t，我们可以表示矩阵 A 的转置。换句话说，我们可以说如果 A^t = [b_ij]，那么 b_ij = a_ij 对于 i = 1, 2, 3, ...., n 和 j = 1, 2, 3, ... , m。

因此，矩阵的转置可以描述为通过交换行和列形成的新矩阵。

因此，

当且仅当 A = A' 时，A 是对称的。

例如：假设有一个矩阵 A，其中

现在我们需要确定该矩阵的转置。

解答：该矩阵的转置通过像这样交换行和列得到

零矩阵

如果一个矩阵的所有元素都为零，则该矩阵称为零矩阵。零矩阵的示例描述如下

对称矩阵

假设有一个方阵 A。如果 A = A^t，则该矩阵称为对称矩阵。

因此，如果 a_ij = a_ij 对于所有 i 和 j，则 A = [a_ij] 是对称的，其中 1 ≤ i ≤ n 且 1 ≤ j ≤ n。

定理

对称矩阵有一些定理，它们描述如下

• 如果存在两个 n∗n 对称矩阵 A 和 B，则 (AB)' = BA。
• 如果存在两个 n∗n 对称矩阵 A 和 B，则 (A+B)' = B+A。
• 如果存在一个任意 n∗n 矩阵 C，则 B = C'C 是对称的。

例如：以下矩阵是对称矩阵

零一矩阵

如果一个矩阵的元素是 0 或 1，则该矩阵称为零一矩阵。我们经常以表格形式使用此矩阵，以便我们可以表示离散结构。如果我们想定义布尔运算，我们可以这样以零一矩阵的形式定义它们的元素

b1 ∧ b2 = 1 if b1 = b2 = 1

0 否则

b1 ∨ b2 = 1 if b1 = 1 or b2 = 1

0 否则

现在我们将以表格形式定义零一矩阵上条目的布尔运算，如下所示

假设有两个 m∗n 的零一矩阵 A 和 B，其中 A = [a_ij] 和 B = [b_ij]。A 和 B 的**连接**（Join）将是一个零一矩阵，其 (i, j) 条目为 a_ij ∨ b_ij。使用符号 A ∨ B，我们可以表示 A 和 B 的**连接**。A 和 B 的**交集**（meet）将是一个零一矩阵，其 (i, j) 条目为 a_ij ∧ b_ij。使用符号 A ∧ B，我们可以表示 A 和 B 的**交集**。

例如：假设有两个矩阵 A 和 B，其中

这些矩阵的**连接**描述如下

这些矩阵的**交集**描述如下

假设有两个矩阵，A = [a_ij] 是一个 m∗k 的零一矩阵，B = [b_ij] 是一个 k∗n 的零一矩阵。A 和 B 的**布尔积**将是一个 m∗n 矩阵，其 (i, j) 条目 [c_ij] 如下

cij = (ai1 ∧ b1j) ∨ (ai2 ∧ b2j) ∨ (ai3 ∧ b3j) ∨ ..... ∨ (aik ∧ bkj)

使用符号 AoB，我们可以表示 A 和 B 的布尔积。

基本上，矩阵乘法和布尔乘法的操作是相似的，但在**布尔乘法**中，我们使用 ∧ 代替乘积，使用 ∨ 代替和。

示例 1：假设有两个矩阵 A 和 B，其中

A 和 B 的布尔乘法描述如下

示例 2：假设有两个矩阵 A 和 B，其中

现在我们需要确定这些矩阵的布尔积。

解答：A 和 B 的乘积描述如下

假设有一个零一矩阵 A 和一个正整数 r。

A 的 r 次布尔幂称为 A 的 r 个因子的布尔积。使用符号 A^[r]，我们可以表示 A 的布尔幂。

A^[0] = I_n,

A^[r] = AoAo .... oA （r 个 A）