Graph

图 G 由两部分组成

1. 一个集合 V=V(G)，其元素称为 G 的顶点、点或节点。

2. 一个集合 E = E(G)，由 G 的不重复顶点的无序对组成，称为 G 的边。

3. 我们用 G(V, E) 表示这样的图。如果存在一条边 e ={u, v}，则称顶点 u 和 v 相邻。

4. 在这种情况下，u 和 v 被称为 e={u, v} 的端点，e 被称作连接 u 和 v。

顶点的度

顶点的度是与顶点 v 相连的边的数量。自环算两次。顶点的度记作 d(v)。

例1： 考虑图 G 所示的图。确定每个顶点的度。

解： 每个顶点的度如下

                  d(a)=3；       d(b)=5；       d(c) = 2；       d(d)=2。

例2： 验证图中所有顶点的度数之和为偶数。

解： 所有顶点的度数之和为

                  =d (v₁)+d(v₂ )+d(v₃ )+d(v₄ )+d(v₅ )+d(v₆ )+d(v₇ )+d(v₈)
                  = 2+3+3+3+3+4+2+2=22，为偶数。

例3： 验证图中度数为奇数的顶点数量为偶数。

解： 度数为奇数的顶点数量为 8，在上面的图中，每个顶点的度数都是 3。因此，我们有偶数个度数为奇数的顶点。

路径

长度为 n 的路径是图中 n+1 个顶点的序列，其中每对顶点都是图中的一条边。

1. 简单路径： 如果路径中没有边重复，则该路径称为简单路径，即除第一个顶点与最后一个顶点相同外，所有顶点都不同。
2. 基本路径： 如果路径中没有顶点重复，则该路径称为基本路径，即所有顶点都不同。
3. 环路或闭合路径： 环路或闭合路径是指起点和终点相同的路径，即 v₀=v_n。
4. 简单环路： 简单环路是作为环路的简单路径。

示例： 考虑图中所示的图：给出以下示例

1. 从 V₁ 到 V₆ 的简单路径。
2. 从 V₁ 到 V₆ 的基本路径。
3. 从 V₁ 到 V₆ 的非基本简单路径。
4. 从 V₂ 开始的非简单路径。
5. 从 V₁ 开始的简单环路
6. 从 V₂ 开始的非简单环路。

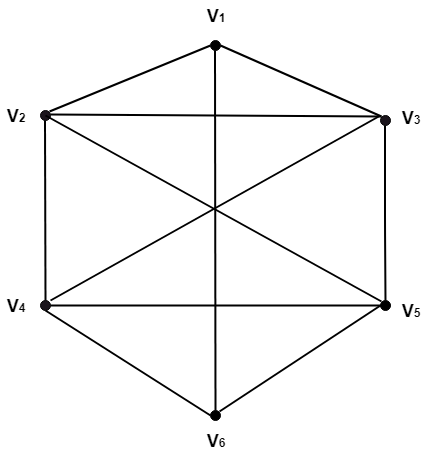解决方案

1. 从 V₁ 到 V₆ 的简单路径。
           V_1,V_2,V_3,V_4,V_5,V₆。
2. 从 V₁ 到 V₆ 的基本路径。
           V_1,V_2,V_3,V_5,V_4,V₆。
3. 从 V₁ 到 V₆ 的非基本简单路径。
           V_1,V_2,V_3,V_5,V_2,V_4,V₆。
4. 从 V₂ 开始的非简单路径。
           V_2,V_3,V_4,V_5,V_3,V_4,V₆。
5. 从 V₁ 开始的简单环路。
           V_1,V_2,V_4,V_6,V_5,V_3,V₁
6. 从 V₂ 开始的非简单环路。
           V_2,V_3,V_1,V_2,V_5,V_4,V₂。

悬挂顶点： 度数为一的顶点称为悬挂顶点。

悬挂边： 唯一与悬挂顶点相连的边称为悬挂边。

奇顶点： 度数为奇数的顶点称为奇顶点。

偶顶点： 度数为偶数的顶点称为偶顶点。

关联边： 边被称为与它所连接的顶点关联。

相邻顶点： 如果有边连接两个顶点，则称这两个顶点相邻。如果存在边 (u, v)，则可以说顶点 u 与顶点 v 相邻，顶点 v 与顶点 u 相邻。

示例： 考虑图中所示的图

确定以下内容

1. 悬挂顶点
2. 悬挂边
3. 奇顶点
4. 偶顶点
5. 关联边
6. 相邻顶点

解决方案

1. 顶点 V₅ 是悬挂顶点。
2. 边 (V_4,V₅) 或 e₅ 是悬挂边。
3. 顶点 V₃ 和 V₅ 是奇顶点。
4. 顶点 V_1, V_2,和 V₄ 是偶顶点。
5. 边 e₁ 与 V_1, 和 V₂ 关联。
       边 e₂ 与 V₁ 和 V₃ 关联。
       边 e₃ 与 V₂ 和 V₃ 关联。
       边 e₄ 与 V₃ 和 V₄ 关联。
       边 e₅ 与 V₄ 和 V₅ 关联。
6. 顶点 V₁ 与 V₂ 和 V₃ 相邻。
       顶点 V₂ 与 V₁ 和 V₂ 相邻。
       顶点 V₃ 与 V₁ 和 V₄ 相邻。
       顶点 V₄ 与 V₃ 和 V₅ 相邻。
       顶点 V₅ 与 V₄ 相邻。

自环： 如果边 e 有相同的端点，则它是一个自环。

图中所示的图在顶点 b 处包含自环，即 e=(b, b)。

孤立顶点：度数为 0 的顶点称为孤立顶点。

割集： 考虑图 G=(V, E)。G 的割集是最小的边集，移除该集合会使图断开连接，而移除该集合的任何真子集则会留下一个连通子图。

示例： 考虑图中所示的图。确定该组的割集。

解： 对于此图，边集 {(V_1,V₅),(V_7,V₅)} 是一个割集。移除该集合后，我们留下了一个断开连接的子图。而移除其任何真子集后，我们留下了一个连通子图。

割点或割顶点： 考虑图 G=(V, E)。图 G 的割点是顶点 v，使得 G-v 比 G 具有更多的连通分量或断开连接。

子图 G-v 是通过从图 G 中删除顶点 v 并同时删除所有与 v 关联的边而获得的。

示例： 考虑图中所示的图。确定子图

(i)G-v₁     (ii) G-v₃     (iii) G-v₅

解决方案

1. 子图 G-v₁ 如图所示
2. 子图 G-v₃ 如图所示
3. 子图 G-v₅ 如图所示

桥（割边）： 考虑图 G=(V, E)。图 G 的桥是边 e，使得 G-e 比 G 具有更多的连通分量或断开连接。

示例： 考虑图中所示的图。确定子图

(i)G-e₁     (ii) G-e₃     (iii) G-e₄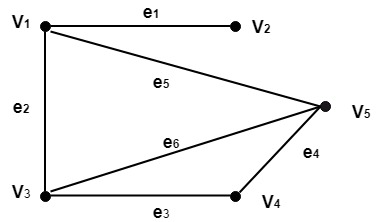

解决方案

1. 子图 G-e₁ 如图所示
2. 子图 G-e₃ 如图所示
3. 子图 G-e₄ 如图所示