离散数学中的初等矩阵

要学习初等矩阵，我们首先要学习矩阵和单位矩阵。之后，我们才能理解初等矩阵的概念。

矩阵

矩阵可以描述为一组数字，这些数字按照行和列排列。这些数字被称为矩阵的项或元素。方括号用于包含这些类型的元素。假设有 n 行和 m 列。在这种情况下，该矩阵将被称为 n×m 矩阵，可以写成“n * m”。还有一个 n×n 的方阵，可以描述为 n 行 n 列的 n 阶集合。

例如：在这个例子中，我们将展示一个 3×3 矩阵。

解答：3×3 矩阵意味着有 3 行和 3 列。也就是说总共有 9 个元素。3×3 矩阵描述如下

单位矩阵

单位矩阵可以描述为任何阶的方阵，其中主对角线上的所有元素都为 1，所有其他元素都为 0。单位矩阵的阶数总是 n。所以我们可以说单位矩阵的维度是 n×n。这意味着此矩阵中的行数和列数始终相等。下面描述了不同维度的单位矩阵的表示。

初等矩阵

初等矩阵也是一种方阵。初等矩阵和单位矩阵是相似的。唯一的区别是，在初等矩阵中，单位矩阵上的三个基本行或列操作中会有一个。初等矩阵中的行操作描述如下：

R1：将一行的元素乘以一个非零实数。

R2：交换两行

R3：将一行的常数 k 倍加到另一行。

这里 R1、R2、R3 用于表示行操作。当我们对任何矩阵应用行操作时，它就被称为初等行操作。相比之下，初等矩阵中的列操作描述如下：

C1：将一列的元素乘以一个非零实数。

C2：交换两列

C3：将一列的常数 k 倍加到另一列。

这里 C1、C2、C3 用于表示列操作。当我们对任何矩阵应用列操作时，它就被称为初等列操作。

我们知道初等矩阵是从单位矩阵得到的，而单位矩阵总是方阵。因此，初等矩阵也总是方阵。

示例：在这个例子中，我们将展示四个初等矩阵以及用于生成这些矩阵的操作。

解决方案

1. 以下矩阵是通过将单位矩阵 (I₂) 的第二行乘以 -3 而生成的。
   
2. 以下矩阵是通过交换单位矩阵 (I₄) 的第二行和第四行而生成的。
   
3. 以下矩阵是通过将单位矩阵 (I₃) 的第三行的三倍加到第一行而生成的。
   
4. 以下矩阵是通过将单位矩阵 (I₃) 的第一行乘以 1 而生成的。
   

通过初等矩阵可以生成可逆矩阵的一般线性群。当初等矩阵执行左乘或预乘时，将表示初等行操作。当初等矩阵执行右乘或后乘时，将表示初等列操作。高斯消元法使用初等行操作，以便将矩阵化为行阶梯形。高斯-约旦消元法也使用初等行操作，以便进一步将矩阵化为行阶梯形。初等行操作的例子如下所示：

示例：在这个例子中，我们将考虑一个矩阵 A，其如下所示：

在这个矩阵 A 中，我们将执行以下初等行操作，如下所示：

在这个初等行操作中，初等矩阵将按以下方式对应：

我们可以看到，当对单位矩阵 I 执行相同的初等行操作时，我们将得到以下矩阵。对矩阵 A 执行 EA 乘法的结果与对矩阵 A 执行初等行操作的结果相同。E 和 A 的乘法描述如下：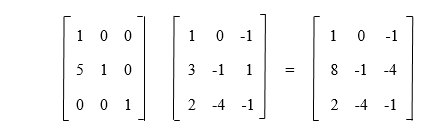

对于其他初等行操作，情况也是如此。我们也可以对每个初等矩阵执行逆操作。如果我们对初等矩阵求逆，它仍然是初等矩阵。我们可以通过对单位矩阵执行逆行操作来证明这个概念。逆行操作描述如下：

• R_i → kR_i 的逆是 R_i → 1/k R_i。
• R_i → kR_j + R_i 的逆是 R_i → −kR_j + R_i。
• R_i ↔ R_j 的逆是 R_i ↔ R_j。

我们可以使用初等矩阵进行初等行变换。它还用于提供一个构造性工具，可以用来找出逆矩阵并确定 LU 分解。初等矩阵及其逆的例子如下所示，我们可以通过将矩阵相乘来检查每个矩阵。如果矩阵是逆的，它们的乘积将是 I。

初等矩阵有一个非常重要的事实，即如果矩阵 A 是可逆的，我们也可以将其写成初等矩阵的乘积。

初等矩阵的性质

所有初等矩阵都是非奇异的。所有非奇异初等矩阵的逆也将是初等矩阵。初等矩阵有各种性质，如下所示：

1. 如果有一个矩阵用于交换两行，那么这个矩阵的逆就是它本身。

例如：假设有一个矩阵，其描述如下：

这个矩阵的逆描述如下：

矩阵的计算描述如下：

2. 如果有一个初等矩阵用于模拟 (mR_i) ↔ (R_i)，那么这类矩阵的逆也将是模拟 (1/m R_i) ↔ (R_i) 的初等矩阵。

例如：假设有一个矩阵，其描述如下：

这个矩阵的逆描述如下：

矩阵的计算描述如下：

3. 如果有一个初等矩阵用于模拟 (R_j + mR_i) ↔ (R_j)，那么这类矩阵的逆也将是模拟 (R_j - mR_i) ↔ (R_j) 的初等矩阵。

例如：假设有一个矩阵，其描述如下：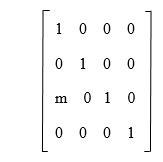

这个矩阵的逆描述如下：

矩阵的计算描述如下：

初等矩阵的例子

示例 1：在这个例子中，我们需要确定给定的矩阵 A 是否为初等矩阵。

解答：如我们所知，初等矩阵总是方阵，而上面的矩阵不是方阵。因此，我们可以说矩阵 A 不是初等矩阵。

示例 2：在这个例子中，我们需要确定给定的矩阵 A 是否为初等矩阵。

解答：2×2 的单位矩阵 (I₂) 描述如下：

如果将单位矩阵 (I₂) 的第二行乘以 -3，我们就能得到上面的矩阵 A。因此，我们可以说矩阵 A 是初等矩阵。

示例 3：在这个例子中，我们需要确定给定的矩阵 A 是否为初等矩阵。

解答：3×3 的单位矩阵 (I₃) 描述如下：

如果我们将 I₃ 的第一行乘以 7，我们将得到以下矩阵：

正如我们所见，这个矩阵不等于给定的矩阵 A，因为矩阵 A 的第三行和生成的矩阵不相同。我们也无法执行单个行或列操作，以便从单位矩阵 I3 得到给定的矩阵 A。因此，我们可以说给定的矩阵 A 无法描述为初等矩阵。