离散数学中的哈希函数17 Mar 2025 | 6 分钟阅读 为了理解哈希函数,我们将首先学习哈希和哈希表。 哈希哈希也称为消息摘要函数或哈希算法。在哈希过程中,我们可以将大型数据项转换为较小的表。我们将使用哈希函数来映射数据。通过哈希,可以将一组键值转换为数组索引的集合。当我们将哈希与二分查找或线性查找进行比较时,哈希提供了一种更高级别的查找方法。 哈希还为我们提供了更新和检索任何数据项的便利,但数据必须在常数时间 O(1) 内输入。常数时间 O(1) 用于表示操作不取决于数据的大小。哈希包含一个数据库,以便可以更快地检索项目。在数字签名的情况下,它也可以用于加密或解密数据。哈希本质上是发生在较大集合和较小集合之间的多对一映射。哈希函数可以用于数据库、内存映射或字典中。 哈希函数哈希函数可以描述为将键转换为哈希键的固定过程。哈希函数接受一个键,并将该键映射到某个长度的值。这种长度称为哈希值或哈希。原始字符被哈希值表示,但这些字符比原始字符短。它也用于传输数字签名。它基本上是将哈希值和签名发送给接收者。接收者使用相同的哈希函数生成哈希值。然后,将生成的哈希值和接收到的哈希值进行比较。如果两个哈希值相同,则表示消息已毫无错误地传输。 在离散数学中,哈希函数可以描述为一个应用于键的函数。该键用于生成一个整数,我们可以将此整数用作哈希表中的地址。换句话说,哈希函数 'h' 用于将内存位置 'h(k)' 分配给包含键 'k' 的记录。在离散数学中,所有内存位置都是可能的。这是因为哈希函数是满射的。一个简单的哈希函数可以定义如下: 这里 m 用于表示内存位置的数量。 哈希表哈希表可以描述为一种数据结构,用于存储键值对。哈希表用于存储键或项目的集合,以便以后可以轻松搜索任何项目。它基本上利用哈希函数计算数组槽或桶的索引。从桶数组中,我们可以轻松找到所需的值。它基本上包含一个列表数组,其中每个列表称为一个桶。它用于根据键包含值。此表是同步的,并且列表中只能有唯一的元素。哈希表描述如下:  在上图中,我们可以看到一个大小为 n = 10 的哈希表。在此表中,每个位置称为一个槽。上表共有 n 个位置,名称为:0、1、2、3、4、5、6、7、8 和 9。我们也可以称之为槽 0、槽 1、槽 2、槽 3 等。这些槽或位置用于存储一些键。在此表中,所有位置/地址/槽都是空的。 正如我们在上面学到的,键与键所属的哈希表位置之间的映射称为哈希函数。哈希函数从集合中选择任何键,并将其放置在 0 到 n-1 之间的槽名范围内。 假设总共有 0、1、2、3、4、5、6、7、8 和 9 这些位置/槽。我们将按以下方式将键 70、31、93、54、26 和 18 分配给这些槽:
这些数据的哈希表描述如下:  因此,我们可以使用哈希函数轻松搜索项目。为此,哈希函数会计算键的位置或槽名。然后,它会检查哈希表,并找出所需键是否存在于表中。在哈希表中,两个键不会存在于同一位置或槽中。 哈希函数示例示例 1:在此示例中,我们将假定 h(k) = k mod 111。客户记录将由以社会安全号码为键的哈希函数分配到内存位置。它将按以下方式完成: 我们可以看到位置 14 已经被占用。因此,记录将被分配到下一个可用位置,即 15。这些记录的哈希表描述如下:  示例 2:在此示例中,我们将使用中国生肖,如鼠、牛、虎、兔等,以便将学生提交的期中考试成绩分到 12 个盒子中。 解决方案:首先,我们将根据生肖为盒子贴标签。所以,鼠 = 0,牛 = 1,虎 = 2,兔 = 3,依此类推。然后,我们将提供盒子编号 (b),以便它可以容纳出生年份 (y) 的学生的期中考试成绩。因此,借助以下公式,期中考试成绩将如下计算: 例如,出生于 2000 年的学生的期中考试成绩将放在下面的盒子中,如下所示: 因此,这将是龙年对应的盒子。 哈希函数用于容纳比内存位置多得多的潜在键,因为它不是一对一的。 冲突还存在一种冲突的情况,当两个或两个以上的记录被分配到同一位置时,就会发生冲突。冲突问题可以通过将记录分配到第一个空闲位置来解决。线性探测函数可用于解决冲突。我们还可以通过使用各种其他方法来处理冲突。与线性冲突解决方法相关的公式描述如下: 在此公式中,i 从 0 运行到 m-1。 示例:在此示例中,我们将有一个包含 11 个整数的数组。 解决方案:如我们所知,h(k) = k mod m,此处 m = 11 所以 首先,哈希表将仅包含地址或槽,如下所示:  现在,我们将键分配给这些地址,如下所示:  在这里,我们可以看到 47、14 和 25 分配到了相同的内存位置 3。在这种情况下,会发生冲突问题,因为一个以上的记录/键被分配到同一位置。为了解决这个问题,我们将为它们分配其他位置。首先,47 将被分配到内存位置 3,14 将被分配到下一个空闲位置,即 4。25 将再次被分配到除了 3 和 4 之外的下一个空闲位置,即 5。所以最后,47 得到位置 3,14 得到位置 4,25 得到位置 5。这些新内存位置的哈希表描述如下: 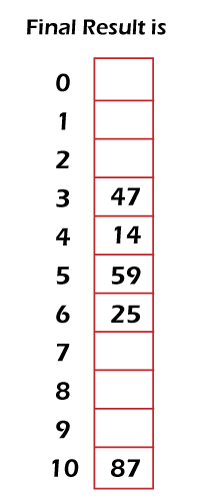 |
我们请求您订阅我们的新闻通讯以获取最新更新。