离散数学中的厄米矩阵

对称矩阵和厄米矩阵都用来包含相似的性质。厄米（Hermitian）这个名字来源于一位著名的数学家查尔斯·埃尔米特。厄米矩阵用来包含其元素形式的复数。**厄米矩阵** 与其**共轭转置矩阵** 相似。矩阵A的共轭转置可以用符号A^H或A\*表示。在本节中，我们将学习厄米矩阵、不同阶数的厄米矩阵、其公式、性质、厄米矩阵的例子等等。

什么是厄米矩阵

如果一个矩阵是方阵，并且与它的共轭转置矩阵相似，那么它就被称为厄米矩阵。对于厄米矩阵，所有**非对角线元素**都包含**复数**，而所有**对角线元素**都包含**实数**。在这类矩阵中，所有复数都以一种方式排列：第i行第j列的元素是第j行第i列元素的复共轭。如果一个数字表示为a+ib，那么这个数字就是复数，其中a表示实部，b表示虚部。

如果一个矩阵满足条件A = A^H，那么它就被称为厄米矩阵。对称矩阵和厄米矩阵都彼此相似，但有一个区别：厄米矩阵用于包含非主对角线元素的复数。

2x2阶的厄米矩阵

对于厄米矩阵，非对角线元素是复数。第一行第一个元素和第二行第二个元素是实数。在这个矩阵中，第一行第二个元素的复数是第二行第一个元素的复共轭。下面是2x2阶厄米矩阵的例子：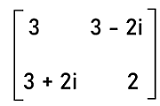

3x3阶的厄米矩阵

对于厄米矩阵，非对角线元素是复数。连接从第一行第一个元素到第三行第三个元素对角线的元素是实数。位于(i, j)位置的元素是位于(j, i)位置元素的复共轭。下面给出了一个表示厄米矩阵的例子：

该矩阵的第一行第二列包含2+i元素，而第二行第一列包含其共轭元素2-i。所有其他复数也将遵循相同的规则。

厄米矩阵的公式

根据上面描述的两个矩阵，我们知道厄米矩阵的对角线元素包含实数。我们还知道位于(i, j)位置的元素是位于(j, i)位置元素的复共轭。因此，2x2厄米矩阵的标准表示形式如下：

这里x、y、z和w表示实数。

同样，3x3阶厄米矩阵的标准表示形式如下：

厄米矩阵的性质

厄米矩阵有多种性质，其中一些如下所述：

• 对于厄米矩阵，所有主对角线元素始终包含实数。
• 非对角线元素必须是复数。
• 如果存在一个厄米矩阵，那么该矩阵必然是一个正规矩阵，即A^H = A。
• 如果我们对两个厄米矩阵进行相加，则结果矩阵将是厄米矩阵。
• 如果我们对两个厄米矩阵进行求逆运算，则结果矩阵将是厄米矩阵。
• 如果我们对两个厄米矩阵进行乘法运算，则结果矩阵将是厄米矩阵。
• 如果我们计算厄米矩阵的行列式，则该矩阵将是实数。
• 厄米矩阵的特征值包含实数。

与厄米矩阵相关的术语

在学习厄米矩阵的概念时，有一些重要的要点需要了解。这些要点如下所述：

主对角线：对于一个方阵，主对角线可以由连接从第一行第一个元素到最后一行最后一个元素的所有对角线元素集合来表示。

对称矩阵：如果一个方阵的转置矩阵与其本身相同，那么它就被称为对称矩阵。

共轭矩阵：如果我们用给定矩阵的对应元素的复共轭来替换给定矩阵的对应元素，那么我们将得到该矩阵的共轭矩阵。

转置矩阵：如果我们交换原矩阵的行或列的元素，那么该矩阵就被称为转置矩阵。假设有一个方阵A。我们可以用符号A^T表示该矩阵的转置。

将矩阵写成厄米矩阵和斜厄米矩阵

如果存在一个方阵，那么我们可以将其写成一个厄米矩阵P和一个斜厄米矩阵Q的相加。通过以下公式，我们可以确定斜厄米矩阵和厄米矩阵的相加。

假设有一个**方阵A**。那么，

A = (1/2) (A + A^H) + (1/2) (A - A^H)。这里A^H表示矩阵A的共轭转置。

• 如果一个厄米矩阵表示为A + A^H，那么(1/2) × (A + A^H)也将表示一个厄米矩阵。
• 如果一个斜厄米矩阵表示为A - A^H，那么(1/2) × (A - A^H)也将表示一个斜厄米矩阵。

因此，如果存在一个方阵，那么我们可以将其写成一个斜厄米矩阵和一个厄米矩阵的相加。

厄米矩阵的例子

有很多厄米矩阵的例子，其中一些如下所述：

例1：在这个例子中，我们有一个矩阵A，我们需要确定它是否是厄米矩阵。矩阵A的元素如下所示：

解答：根据题目，我们有矩阵A

现在我们将对该矩阵进行共轭运算，如下所示：

现在我们将对A的共轭进行转置，如下所示：

因此，给定的矩阵A是厄米矩阵。

例2：在这个例子中，我们有一个厄米矩阵，我们需要证明该矩阵的行列式始终为实数。

解答：为此，我们将假设一个2x2的厄米矩阵，并计算其行列式。

det A = xw - (y + zi)(y - zi)

= xw - (y²- z²i²)

= xw - (y²+ z²)

= xw - y²- z²

= 一个实数

同样，我们可以假设一个其他阶数的厄米矩阵，并发现该矩阵的行列式也是一个实数。

因此，证明了厄米矩阵的行列式始终为实数。

例3：在这个例子中，我们有两个厄米矩阵，我们需要计算这两个矩阵的相加。我们还需要证明这个加法的结果也是一个厄米矩阵。这两个厄米矩阵的元素如下所示：

解答：根据题目，我们有两个厄米矩阵，并将它们相加如下：

现在我们将对上述相加(A+B)进行共轭运算，如下所示：

现在我们将对A+B的共轭进行转置，如下所示：

证明了两个厄米矩阵的相加也是厄米矩阵。

例4：在这个例子中，我们有一个矩阵A，我们需要确定它是否是厄米矩阵。矩阵A的元素如下所示：

解答：根据题目，我们有一个厄米矩阵，它表示如下：

现在我们将对矩阵A进行共轭运算，如下所示：

现在我们将对A进行共轭转置(A\*)，如下所示：

这里我们可以看到，A的共轭转置与给定的矩阵A相似。因此，这是一个厄米矩阵。

例5：在这个例子中，我们有一个厄米矩阵A和一个复数x。这里我们需要确定x乘以A是否会得到一个厄米矩阵。

解答：根据题目，我们知道存在一个复数x和一个厄米矩阵A，即A\* = A。

xA的乘积是厄米矩阵，如果它满足以下条件：

(xA)\* = xA

现在：

(xA) = x̅A\* = x̅A ≠ xA

因为x表示复数，它与其共轭不相似。

因此

(xA)\* = xA

因此，xA不是厄米矩阵。