恒等函数2025 年 3 月 17 日 | 阅读 1 分钟 如果集合 A 的每个元素都有其自身的像,即 f(a) = a ∀ a ∈ A,则函数 f 称为恒等函数。 它用 I 表示。 示例 函数 f 是一个恒等函数,因为 A 的每个元素都映射到自身。函数 f 是一个单射且满射的。  可逆(逆)函数当且仅当函数 f: X → Y 是一个双射函数时,它才是可逆的。 考虑双射(一对一和满射)函数 f: X → Y。 由于 f 是一对一的,因此 X 的每个元素对应于 Y 的一个不同的元素。由于 f 是满射的,Y 中没有元素不是 X 的任何元素的像,即,范围 = 共域 Y。 如果 f-1 是一个从 Y 到 X 的函数,则 f 的逆函数存在。 示例 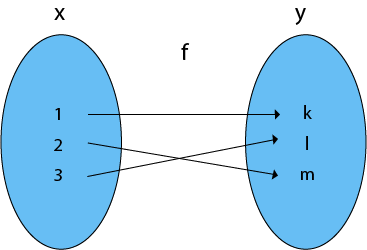 f 的逆函数如图所示  下一主题函数复合 |
以下是计算机科学中广泛使用的函数。1. Floor 函数:任何实数 x 的 floor 函数定义为 f (x) 是小于或等于 x 的最大整数 1。它表示为 [x]。示例:确定值...
阅读 2 分钟
算法和函数 算法:算法是解决某些问题的一种逐步方法。 算法的特点:算法通常具有以下特点: 输入:算法接收输入。 外部提供零个或多个量。 输出:算法产生输出。 产生至少一个量。 精度:步骤被精确地陈述...
阅读 3 分钟
1. 单射(一对一)函数:一个定义域集合的一个元素连接到共域集合的一个元素的函数。 2. 满射(映上)函数:共域集合的每个元素都有一个原像的函数。 示例: 考虑,A = {1, 2, 3, 4},B =...
阅读 3 分钟
它是一种映射,其中集合 A 的每个元素与集合 B 中的元素唯一关联。集合 A 称为函数的定义域,集合 B 称为共域。函数的定义域、共域和值域:定义域...
阅读 3 分钟
函数复合 考虑函数 f: A B 和 g: B C。 f 和 g 的复合是从 A 到 C 的一个函数,定义为 (gof) (x) = g [f(x)],并由 gof 定义。 找到 f 的复合...
阅读 2 分钟
我们请求您订阅我们的新闻通讯以获取最新更新。

我们提供所有技术(如 Java 教程、Android、Java 框架)的教程和面试问题
G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India
