离散数学中的图同构

同构图可以描述为一种图，其中单个图可以有多种形式。这意味着两个不同的图可以具有相同数量的边、顶点和相同的边连通性。这类图被称为同构图。同构图的例子如下：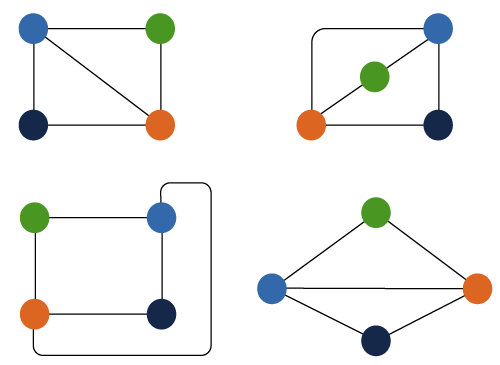

上面的图包含以下内容：

• 同一个图以多种形式表示。
• 因此，我们可以说这些图是同构图。

图同构的条件

任何两个图，如果满足以下四个条件，则被称为同构图：

1. 给定的图中顶点的数量相等。
2. 给定的图中边的数量相等。
3. 给定的图中度数序列相等。
4. 如果第一个图通过顶点 {v1, v2, v3, …. vk} 形成一个长度为 k 的环，则另一个图也必须通过顶点 {v1, v2, v3, …. vk} 形成相同长度为 k 的环。

注意：图的度数序列可以描述为图中所有顶点的度数按升序排列的序列。

重要提示

• 为了使两个图同构，上述四个条件是必要条件。
• 上述条件不一定足以证明给定的图是同构的。
• 如果两个图满足上述四个条件，即使如此，也不能保证这两个图一定是同构的。
• 如果图未能满足任何条件，那么我们可以说这两个图肯定不是同构的。

图同构的充分条件

如果我们想证明两个图是同构的，有一些充分条件可以保证这两个图一定是同构的。当两个图成功通过上述所有四个条件后，我们才会检查这些图是否满足充分条件，这些条件如下：

• 如果两个图的补图是同构的，那么这两个图一定也是同构的。
• 如果两个图的邻接矩阵相同，则这两个图是同构的。
• 如果通过删除一个图的某些顶点得到另一个图的对应图，并且它们的对应图像是同构的，那么这两个图就不是同构的。

当两个图满足上述任何条件时，我们可以说这两个图一定是同构的。

图同构的例子

有很多图同构的例子，如下所示：

示例 1

在这个例子中，我们展示了以下图是否是同构图。

解：为此，我们将检查图同构的所有四个条件，如下所示：

条件 1

• 在图 1 中，总共有 4 个顶点，即 G1 = 4。
• 在图 2 中，总共有 4 个顶点，即 G2 = 4。

此处，

两个图 G1 和 G2 具有相同数量的顶点。因此，这些图满足条件 1。现在我们将检查第二个条件。

条件 2

• 在图 1 中，总共有 5 条边，即 G1 = 5。
• 在图 2 中，总共有 6 条边，即 G2 = 6。

此处，

两个图 G1 和 G2 的边数不相等。因此，这些图不满足条件 2。现在我们无法检查所有剩余的条件。

由于这些图违反了条件 2。因此，这些图不是同构图。

∴ 图 G1 和图 G2 不是同构图。

示例 2

在这个例子中，我们展示了以下图是否是同构图。

解：为此，我们将检查图同构的所有四个条件，如下所示：

条件 1

• 在图 1 中，总共有 4 个顶点，即 G1 = 4。
• 在图 2 中，总共有 4 个顶点，即 G2 = 4。
• 在图 3 中，总共有 4 个顶点，即 G3 = 4。

此处，

所有图 G1、G2 和 G3 都具有相同数量的顶点。因此，这些图满足条件 1。现在我们将检查第二个条件。

条件 2

• 在图 1 中，总共有 5 条边，即 G1 = 5。
• 在图 2 中，总共有 5 条边，即 G2 = 5。
• 在图 3 中，总共有 4 条边，即 G2 = 4。

此处，

• 两个图 G1 和 G2 具有相同数量的边。因此，这些图满足条件 2。
• 但是图 (G1, G2) 和 G3 的边数不相等。因此，图 (G1, G2) 和 G3 不满足条件 2。

由于图 (G1, G2) 和 G3 违反了条件 2。因此，我们可以说这些图不是同构图。

∴ 图 G3 与图 G1 或图 G2 都不是同构图。

由于图 G1 和 G2 满足条件 2。因此，我们可以说这些图可能是同构的。

∴ 图 G1 和 G2 可能是同构图。

现在我们将检查图 G1 和 G2 的第三个条件。

条件 3

• 在图 1 中，度数序列 s 为 {2, 2, 3, 3}，即 G1 = {2, 2, 3, 3}。
• 在图 2 中，度数序列 s 为 {2, 2, 3, 3}，即 G2 = {2, 2, 3, 3}。

其中

两个图 G1 和 G2 具有相同的度数序列。因此，这些图满足条件 3。现在我们将检查第四个条件。

条件 4

图 G1 通过顶点 {2, 3, 3} 形成一个长度为 3 的环。

图 G2 也通过顶点 {2, 3, 3} 形成一个长度为 3 的环。

此处，

这表明两个图包含相同的环，因为两个图 G1 和 G2 都通过顶点 {2, 3, 3} 形成一个长度为 3 的环。因此，这些图满足条件 4。

因此，

• 图 G1 和 G2 满足上述所有四个必要条件。
• 因此，G1 和 G2 可能是同构图。

现在我们将检查充分条件，以证明图 G1 和 G2 是同构图。

检查充分条件

正如我们所学到的，如果两个图的补图是同构的，那么这两个图一定是同构的。

因此，我们将绘制 G1 和 G2 的补图，如下所示：

在上面的 G1 和 G2 的补图中，我们可以看到这两个图是同构的。

∴ 图 G1 和 G2 是同构图。

示例 3

在这个例子中，我们展示了以下图是否是同构图。

解：为此，我们将检查图同构的所有四个条件，如下所示：

条件 1

• 在图 1 中，总共有 8 个顶点，即 G1 = 8。
• 在图 2 中，总共有 8 个顶点，即 G2 = 8。

此处，

两个图 G1 和 G2 具有相同数量的顶点。因此，这些图满足条件 1。现在我们将检查第二个条件。

条件 2

• 在图 1 中，总共有 10 条边，即 G1 = 10。
• 在图 2 中，总共有 10 条边，即 G2 = 10。

此处，

两个图 G1 和 G2 具有相同数量的边。因此，这些图满足条件 2。现在我们将检查第三个条件。

条件 3

• 在图 1 中，度数序列 s 为 {2, 2, 2, 2, 3, 3, 3, 3}，即 G1 = {2, 2, 2, 2, 3, 3, 3, 3}。
• 在图 2 中，度数序列 s 为 {2, 2, 2, 2, 3, 3, 3, 3}，即 G2 = {2, 2, 2, 2, 3, 3, 3, 3}。

其中

两个图 G1 和 G2 具有相同的度数序列。因此，这些图满足条件 3。现在我们将检查第四个条件。

条件 4

• 图 G1 通过度数为 3 的顶点形成一个长度为 4 的环。
• 图 G2 由于顶点不相邻，因此不通过长度为 4 的环。

此处，

图 G1 和 G2 都不能用相同长度的相同环形成。因此，这些图违反了条件 4。

由于图 G1 和 G2 违反了条件 4。因此，由于违反了条件 4，这些图不会是同构图。

∴ 图 G1 和 G2 不是同构图。