离散数学中的有向图和无向图

为了学习离散数学中的有向图和无向图，我们将首先学习图。之后，我们将学习有向图和无向图。图的描述如下：

Graph

图是代表一组顶点和边的数学和图形表示。它由非空集合组成，其中边与节点或顶点连接。节点可描述为代表对象的顶点。边可称为对象之间的连接。箭头（→）用于表示边。根据箭头的方向，图会进行遍历。图的边有时包含权重，用于显示顶点之间每个连接的强度。

基于边的不同，对不同类型的图有不同的正式定义。因此，产生了各种术语。在各种应用中，节点和边的定义不同。例如：借助图，我们可以模拟社交网络的友谊。在图中，人将用节点表示，友谊将用边表示。

借助图，我们可以对各种系统进行建模。机场和网页链接是一个很好的例子。对于机场，机场将由节点表示，机场之间的航线将由边表示。在使用图时，我们应该了解一些定义，这些定义对我们很有用。这些定义如下：

• 自环可描述为连接顶点与其自身的边。子图是构成有向图的有向图边集的子集。
• 如果图的两条边连接同一对有序顶点，则这些边是平行的。边的数量也可以称为环或路径的长度。顶点的出度可描述为从它指向的边的数量。顶点的入度可描述为指向它的边的数量。
• 在有向图中，有向路径可描述为顶点序列和有向边。其中，边从序列中的每个顶点指向其后继。有向路径不包含重复的边。如果没有重复的顶点，则有向路径是简单的。
• 如果所构成的有向路径的第一个和最后一个顶点相同，并且包含至少一条边，则该有向路径称为有向环。如果在有向环中除了第一个和最后一个顶点必需的重复之外没有其他重复的顶点，则该有向环是简单的。如果不存在有向环，则该有向图称为有向无环图 (DAG)。
• 假设有两个顶点“x”和“y”。如果存在从“x”到“y”的有向路径，则顶点“x”可从顶点“y”到达。如果顶点“x”和“y”都相互可达，则这些顶点称为强连通。相互可达意味着顶点“x”有从顶点“y”的有向路径，并且顶点“y”也有从顶点“x”的有向路径。
• 如果每个顶点都有通往每个其他顶点的有向路径，则该有向图将是强连通的。如果该有向图不是强连通的，它将包含一组强连通分量。这类分量是极大的、强连通的子图。

图的类型

现在我们将描述两种图：有向图，无向图。

有向图

有向图也称为数字图，它是一组顶点和边的集合。这里的边是有向边，每条边都连接着一对有序的顶点。在图中，有向边或箭头从对中的第一个/原始顶点指向第二个/目标顶点。在 V 顶点图中，我们将用 0 到 V-1 的名称来表示顶点。如果在有向图中存在连接顶点 x 和 y 的边 (x, y)，则不一定存在边 (y, x)。

根据有向图的定义，不允许同一源节点和目标节点有多于一条箭头，但一些作者考虑了边界定义，他们认为同一源节点和目标节点可以在有向图中包含多条箭头，因为它们允许箭头集成为多重集。更具体地说，我们可以将这类实体称为有向多重图。

根据上述有向图的定义，数字图允许自环。这意味着它们可以包含直接连接节点到自身的箭头。如果该有向图有自环，则该图称为自环数字图。在下面的有向图中，只有有向边。它包含从一个顶点到任何其他顶点的有向边和一个自环。

一些作者允许一个更狭窄的定义，即数字图不允许包含自环。更具体地说，如果数字图不包含自环，则该图称为简单有向图。在下面的有向图中，只有有向边。它包含从一个顶点到任何其他顶点的有向边，并且不允许自环。

因此，我们可以说，简单数字图没有任何类型的自环，而任何状态都可以包含从多个顶点（转换）到多个状态。因此，在顶点 x 和 y 中，有向图只能从顶点 x 到顶点 y 进行一次转换，反之亦然。

示例 1

在这个例子中，图可以从顶点 X 遍历到顶点 Y，但不能从顶点 Y 遍历到顶点 X。

示例 2

在这个例子中，我们将考虑图 G = {N, E}。现在我们需要找出图中顶点和边的集合。

对于上面的图，顶点集和边集描述如下：

G = {{1, 2, 3}, {(1, 2), (2, 1), (2, 2), (2, 3), (1, 3)}}

示例 3

上述有向图的邻接矩阵描述如下：

有向图的邻接表描述如下：

无向图

无向图也称为双向图。它是一组对象（也称为顶点或节点），它们相互连接。这里的边是双向的。两个节点用一条线连接，这条线称为边。无向图表示为 G = (N, E)。其中 N 用于表示边集，E 用于表示无序元素对 N 的边集。有向图和无向图的主要区别在于，有向图使用箭头或有向边连接两个节点。在有向图中，箭头从原始顶点指向目标顶点。而在无向图中，两个节点通过两条方向的边连接。

与有向图相比，无向图的限制更多，因为如果关系具有层次性，则无向图不允许对其进行建模。无向图在实践中非常常见。借助无向图，我们可以轻松地对许多现实世界的关系进行建模。例如，“是某人的朋友”的关系可以称为典型的对称关系。这种关系是对称的，因为如果存在“玛丽是哈里的朋友”这种情况，那么“哈里是玛丽的朋友”也是真的。

示例 1

在这个例子中，图可以从顶点 X 遍历到顶点 Y，也可以从顶点 Y 遍历到顶点 X。它可以双向遍历。

示例 2

在这个例子中，我们将假设一个图 G = {N, E}。其中 N = {1, 2, 3, 4}，E = {(1, 2), (1, 4), (3, 4), (2, 3)}。现在我们需要为这些顶点和边绘制一个图。

还有一种方法可以使用给定的顶点和边绘制无向图。

示例 3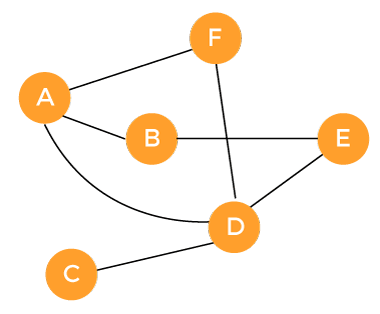

上述无向图的邻接矩阵描述如下：

无向图的邻接表描述如下：

在计算机科学领域，最流行的无向图可以由计算机网络中的连接拓扑来表示。如果图中的一个系统连接到另一个系统，那么在无向图中，第二个系统也将连接到第一个系统。

数字社交网络的拓扑也是无向图的一个著名例子。其中，某人的每个朋友也是某人的朋友。但也有人行道。这意味着路径的两个交叉点可以双向移动。

选择有向图还是无向图

在这里，我们将描述一些有助于我们选择有向图或无向图的要点。

如果网络稀疏，在这种情况下，有向图比相应的无向图信息更丰富。这意味着，如果将稀疏有向图视为无向图，则丢失信息的可能性会增加。

性质非互惠且具有方向性的关系可以用有向图来建模。“是某人的孩子”关系是有向图的一个著名例子，因为借助这种关系，我们可以构建家谱。

无向图用于对那些重要性在于图是否存在的关系进行建模，但它们本身不是传递的。人行道是无向图的一个很好的例子，因为在人行道上，我们可以双向通行。这就是为什么我们可以用无向图来模拟路径。

在某些情况下，我们可以借助有向图对同一个系统进行建模。在另一种情况下，它将被建模为无向图。如果我们学习后代，可以用有向图来表示家庭。在另一种情况下，如果我们对学习家族归属感兴趣，可以用无向图来表示。

程序员必须根据问题仔细选择有向图和无向图，因为这两种图都是对现实世界现象的数学抽象。根据关系，我们将使用图来对其进行建模。如果它是互惠的，那么我们将使用无向图。否则，我们将使用有向图。