离散数学中的矩阵逆

如果我们想确定一个矩阵的逆，那么我们首先需要了解矩阵。矩阵可以被描述为按行和列排列的对象的集合。我们可以称这些类型的对象为矩阵的元素。我们可以用行数乘以列数来表示任何矩阵的阶。例如：2*2，3*3，2*3，等等。

只有当给定的矩阵是方阵时，我们才能确定该矩阵的逆。如果一个矩阵的行数和列数相同，我们就称它为方阵，即2*2，3*3，4*4等。换句话说，逆矩阵可以被描述为通过将矩阵的伴随矩阵除以该矩阵的行列式得到的矩阵。在本节中，我们将学习矩阵的逆，寻找逆矩阵的不同方法的使用，它的性质和例子。

矩阵的逆

假设有一个非奇异方阵 A。矩阵 A 的逆用 A^-1 表示。逆矩阵必须满足一些性质，如下所述：

1. 如果我们将矩阵 A 及其逆矩阵 A^-1 相乘，则乘积结果将是一个单位矩阵。

AA-1 = A-1A = I, 

'I' 用于表示单位矩阵。

例如：假设有一个 2*2 矩阵。该矩阵的单位矩阵如下所示：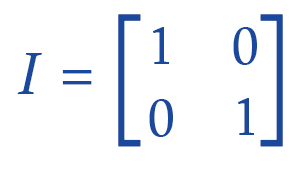

在进行此操作时，我们通常会得到像 4 或 -7 这样的数字。当我们尝试求这些类型的数字的逆时，其逆将是 1/4 或 -1/7，当我们用数字 4 或 -7 乘以这些数字时，结果将得到单位数。

2. 如果有一个方阵，并且我们想计算其逆矩阵，那么该矩阵必须是非奇异的，并且该矩阵的行列式值必须不等于 0。

例如：假设有一个方阵 A，如下所示：

这里，a, b, c 和 D 用于表示数字。

在上述矩阵中，行列式可以写成 ad-bc。为了使逆矩阵存在，行列式的值必须不等于 0。对于 2*2、3*3、4*4、... n*n 矩阵，我们可以找到矩阵的逆。如果我们尝试找到 2*2 矩阵的逆，那么它将比找到 3*3 矩阵的逆简单。

矩阵求逆方法

我们有三种不同的方法可以用来求矩阵的逆。这三种方法都会产生相同的输出。

方法 1

通过以下公式，我们可以求矩阵的逆：

类似地，如果我们确定一个给定的 3*3 矩阵的行列式值，那么我们将能够确定 3*3 矩阵的逆。

方法 2

这种方法是确定逆矩阵最重要和最有用的方法。通过确定给定矩阵元素的代数余子式和余子式，我们可以确定矩阵的逆。现在我们将通过以下步骤来理解这种方法：

• 以下方程也可用于确定逆矩阵：

其中 det(A) 用于表示矩阵 A 的行列式，adj(A) 用于表示矩阵 A 的伴随矩阵。

• 通过以下方法，我们可以确定 adj(A) 或矩阵的伴随矩阵。

我们可以通过首先确定给定矩阵的代数余子式矩阵，然后对代数余子式矩阵进行转置来确定矩阵 A 的伴随矩阵。

• 通过以下公式，我们可以计算矩阵的代数余子式：

Cij = (-1)i+j det(Mij)

这里 Mij 用于表示当移除第 i 行和第 j 列时的 (i, j)^th 代数余子式矩阵。矩阵 A 的伴随矩阵也称为代数余子式矩阵的转置。

类似地，如果我们想确定一个 3*3 矩阵，我们也可以这样做。在 3*3 矩阵中，我们的第一步是确定行列式，第二步是转置。

方法 3

在这种方法中，我们将假设三个矩阵 X、A 和 B，使得 X = AB。借助初等矩阵，我们可以求矩阵的逆。在此过程中，我们将给定的矩阵转换为单位矩阵。

如果存在矩阵 A 的逆矩阵 A^-1，那么我们可以通过初等行变换来找到 A^-1，如下所示：

• 首先，我们将写成 A = IA，其中 'I' 用于表示与 A 同阶的单位矩阵。
• 在矩阵的左侧 (LHS) 应用一系列**行变换**，直到得到单位矩阵。之后，我们将在右侧 (RHS) 应用相同的初等变换，以便得到 I = BA。因此，矩阵 A 的逆由 RHS 上的矩阵 B 表示。
• 现在，我们将使用列变换来求矩阵 A 的逆。为此，我们将写成 A = IA 并按顺序进行列变换，直到得到 I = AB。这里 B 用于表示 A 的逆。

矩阵求逆公式

假设有一个 2*2 矩阵，如下所示：

通过以下公式，我们可以求 2*2 矩阵的逆：

现在我们假设一个 3*3 矩阵，如下所示：

通过以下公式，我们可以通过这种方式求 3*3 矩阵的逆：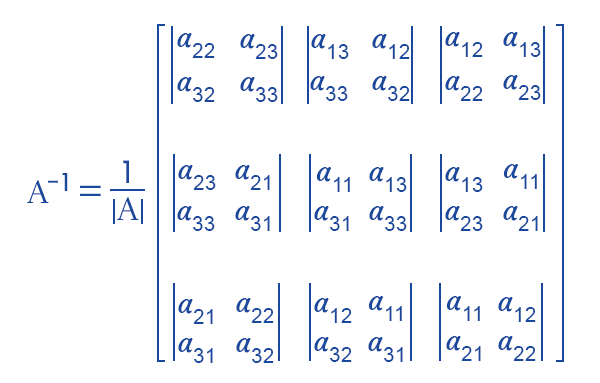

矩阵求逆示例

现在我们将使用以下示例来理解矩阵的逆。

示例 1：在此示例中，我们将求一个 2*2 矩阵的逆，该矩阵如下所示：

解：假设 A = IA

现在我们将对上述矩阵应用 R1 → (1/2)R1 并得到如下结果：

我们将对上述矩阵应用 R2 → R2 - 7R1 并得到如下结果：

现在我们将对上述矩阵应用 R2 → 2R2 并得到如下结果：

我们将应用 R1 → R1 - (1/2)R2 并得到如下结果：

因此，我们将得到矩阵 A 的逆，如下所示：

I = A^-1A。

因此，

示例 2：在此示例中，我们将求一个 3*3 矩阵的逆，该矩阵如下所示：

解决方案

首先，我们将如下所示地表示上述矩阵的行列式：

= 1.33 - 2(-6) +3(-27)

= -36

现在我们将如下所示地确定给定矩阵的代数余子式：

现在我们将使用给定矩阵的代数余子式矩阵的转置来尝试确定矩阵的伴随矩阵，如下所示：

现在，

A^-1 = (1 / |A|) Adj A

因此，我们将得到给定矩阵 A 的逆，如下所示：

矩阵求逆的性质

逆矩阵有一些重要的性质，如下所述：

• 如果存在一个非奇异矩阵 A，则 (A^-1)^-1 = A。
• 如果存在两个非奇异矩阵 A 和 B，则 AB 也是非奇异的。因此，(AB)^-1 = B^-1A^-1
• 如果存在一个非奇异矩阵 A，则 (A^T)^-1 = (A^-1)^T
• 如果存在矩阵 A 及其逆矩阵 A^-1，在此情况下，AA^-1 = A^-1A = I_n。其中 n 用于表示矩阵的阶。

与逆矩阵相关的问题

当我们学习矩阵的逆时，一个问题出现在我们脑海中：“是否可以对每个矩阵求逆？”

解：为了理解这个概念，我们将以数字 0 为例。如果我们将 0 乘以任何数字，那么我们永远不会得到 1。这意味着数字 0 没有乘法逆。

同样，并非所有矩阵都有其逆。只有当给定的矩阵是方阵时，才可能存在逆矩阵，即使如此，也不能保证给定的矩阵是可逆的。如果一个矩阵的行数和列数相同，我们就称它为方阵。当谈论一个矩阵是否有逆时，我们可以使用以下术语：

• 如果一个矩阵有逆，那么该矩阵就被称为非奇异矩阵、可逆矩阵或不太常见的说法。
• 如果一个矩阵没有逆，那么它就被称为奇异矩阵或不可逆矩阵。

通常，我们无法通过观察矩阵来判断它是否可逆。我们可以通过以下示例来理解这一点：

上述矩阵是不可逆的。这是因为不存在任何矩阵可以与此矩阵相乘得到单位矩阵。