离散数学中的行列式

行列式可以被描述为标量，是通过按照规定的规则将方阵的元素与其代数余子式的乘积相加而得到的。借助行列式，我们可以确定矩阵的伴随矩阵、逆矩阵等等。在行列式中，水平线用于表示行，垂直线用于表示列。如果一个行列式是 n 阶的，那么它将有 n 行和 m 列。

例如：假设有两个矩阵，描述如下

该矩阵的行列式描述如下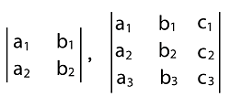

在此示例中，我们有两个行列式，其中第一个行列式是 2 阶的，第二个行列式是 3 阶的。如果有一个 n*n 阶的方阵 A，那么必定有一个与之关联的数，这个数被称为方阵的行列式。例如：

1. 如果一个矩阵是 1*1 阶的，那么它的行列式将是 A = [a]。

2. 假设有一个 2*2 阶的矩阵

这个 2*2 矩阵的行列式将是 ad - bc。

3. 假设有一个 3*3 阶的矩阵

这个矩阵的行列式将是 a(ei − fh) − b (di − fg) + c (dh − eg)。

注意：如果一个行列式是 n 阶的，那么元素的数量将是 n²。

什么是行列式

行列式可以被描述为矩阵的缩放因子。这个矩阵可以被看作是一个用于收缩和拉伸矩阵的函数。就像函数一样，行列式以方阵作为输入，并返回一个单一的数字作为其输出。

行列式的定义

假设有一个 n*n 阶的方阵 C = [cij]。该矩阵的行列式可以定义为一个标量值，它可以是实数或复数。这里的 cij 表示矩阵 C 的第 (i, j) 个元素。矩阵 C 的行列式将表示为 |C| 或 det(C)。我们使用数字网格来书写行列式，并将这些数字排列在绝对值符号内，而不是使用方括号。

例如：假设有一个矩阵 C，其中

这个矩阵的行列式可以写成以下方式

如何计算行列式

如果是一个简单的 1*1 阶方阵，这种情况下，矩阵只有一个数字，该矩阵的行列式就是这个数字本身。现在我们将看看 2 阶、3 阶和 4 阶的矩阵，以及我们如何计算这些矩阵的行列式。

计算 2*2 矩阵的行列式

有一个行列式公式，可以用来确定任何 2D 方阵或任何包含 2*2 阶的方阵的行列式。为此，我们假设一个 2*2 阶的方阵

我们可以用以下方式计算 2*2 矩阵的行列式或 2D 行列式

|C| = (a*d - b*c)

例如

现在我们将用以下方式计算它的行列式

|C| = (8*4) - (6*3)

|C| = 32 - 18

|C| = 14

计算 3*3 矩阵的行列式

我们有一个行列式公式，它将有助于计算 3*3 方阵的行列式。假设有一个包含 3*3 阶的方阵

我们可以用以下方式表示这个矩阵的行列式

我们可以通过一些步骤来计算 3*3 矩阵的行列式，具体描述如下

• 在上述矩阵中，a1 被固定为锚点数，并乘以其子矩阵的 2*2 行列式（a1 的余子式）。
• 用同样的方法，我们可以找到 b1 和 c1 的余子式。
• 现在我们将矩阵的小行列式乘以锚点数及其符号，如下所示
  
• 最后一步，我们将它们相加，如下所示
  
  |C| = a1(b2c3 - b3c2) - b1(a2c3 - a3c2) + c1(a2b3 - a3b2)

现在我们通过一个例子来理解它。假设我们有一个 3*3 矩阵 B，其中

现在我们将按以下方式计算该矩阵的行列式

= 3 × ((-2)(7) - (5)(8)) -1 × ((4)(7) - (5)(2)) + 1 × ((4)(8) - (-2)(2))

= 3 × ((-14) - (40)) -1 × ((28) - (10)) + 1 × ((32) - (-4))

= 3 × (-54) -1 × (18) + 1 × (36)

= - 162 - 18 + 36

= -144

在这个例子中，我们使用第一行来计算 3*3 矩阵的行列式。但我们也可以使用任何行或列来确定该矩阵的行列式。

注意：总而言之，我们可以说确定 3*3 矩阵行列式的公式描述如下：|C| = a1(b2c3 - b3c2) - b1(a2c3 - a3c2) + c1(a2b3 - a3b2)

计算 4*4 矩阵的行列式

假设有一个包含 4*4 阶的方阵或一个 4D 方阵。当我们尝试计算 4*4 矩阵的行列式时，有一些变化我们应该记住。这个 4*4 矩阵和这些变化描述如下

• 如果我们删除包含元素 a1 的行和列，我们可以得到 3*3 矩阵的行列式，然后乘以 a1。
• 如果我们删除包含元素 b1 的行和列，我们可以得到 3*3 矩阵的行列式，然后减去 b1 乘以它。
• 如果我们删除包含元素 c1 的行和列，我们可以得到 3*3 矩阵的行列式，然后乘以 c1。
• 如果我们删除包含元素 d1 的行和列，我们可以得到 3*3 矩阵的行列式，然后减去 d1 乘以它。

我们也可以使用我们在上面主题“计算 3*3 矩阵的行列式”中学到的方法来找到 3*3 矩阵的行列式。这里我们将展示一种非常简单的方法来找到 3*3 矩阵的行列式，描述如下

行列式的乘法

我们可以使用一种称为数组乘法的方法来乘以两个方阵的行列式。现在我们将使用行列相乘的规则来乘以两个不同阶的方阵 A 和 B 的行列式。

2*2 行列式的乘法

这里我们假设两个 2*2 阶的方阵 A 和 B。我们可以分别用符号 |A| 和 |B| 来表示这些矩阵的行列式。乘以这些行列式的过程描述如下

3*3 行列式的乘法

这里我们假设两个 3*3 阶的方阵 C 和 D。我们可以分别用符号 |C| 和 |D| 来表示这些矩阵的行列式。乘以这些行列式的过程描述如下

当我们尝试乘以两个行列式时，有一些要点我们应该记住。这些要点描述如下

• 当且仅当两个行列式具有相同的阶数时，我们才能将它们相乘。
• 如果我们交换行和列，行列式的值不会改变。因此，我们可以使用列乘列、行乘行或列乘行的乘法规则来乘以两个行列式。

行列式的性质

假设有一些不同类型的方阵。如果我们尝试计算它们的行列式，有一些重要的行列式性质需要遵循。我们列出了行列式的重要性质，其中一些描述如下

性质 1：“如果有一个单位矩阵，那么它的行列式总是 1”。

证明：为此，我们假设一个单位矩阵 I，其中

该矩阵的行列式描述如下

|I| = (1)(1) - (0)(0) = 1

因此，任何单位矩阵的行列式总是 1。

性质 2：“如果有一个 n*n 阶的方阵 B，并且该矩阵包含一个全零行或全零列，那么该矩阵的行列式将为 0，即 det(B) = 0”。

证明：为此，我们假设一个方阵 B 的行列式如下

|B| = (2)(0) - (2)(0) = 0。

在上面的方阵 B 中，我们有一行是全零的。因此矩阵 B 的行列式为 0。

性质 3：“如果有一个矩阵 C 是上三角矩阵或下三角矩阵，那么该矩阵的行列式将是其所有对角线元素的乘积”。

证明：为此，我们假设一个上三角矩阵 C，其对角线元素为 3、2 和 4。矩阵 C 的行列式描述如下

|C| = 3*2*4 = 24

因此 C 的行列式为 24。

性质 4：如果有一个方阵，并且该矩阵的一行乘以一个常数 k，在这种情况下，常数 k 可以从行列式中提出。

证明

|D| = (2)(5) - (4)(1) |D| = 10 - 4 = 6	|D| = 2* {(1)(5) - (2)(1)} |D| = 2* (5-2) =2*3 = 6

在这两个矩阵中，我们可以看到行列式保持不变。

还有一些其他重要的行列式性质，描述如下

• 如果有一个方阵，当且仅当 det(C) ≠ 0 时，它才是可逆的。
• 如果有两个 n*n 阶的方阵 A 和 B，则 det(BC) = det(B) * det(C) = det(C) * det(B)。
• 我们可以用以下方式表示矩阵 D 的行列式与其伴随矩阵之间的关系：D * adj(D) = adj(D) * D = |D| * I。这里 I 用于表示单位矩阵，D 用于表示方阵。

行列式运算规则

如果我们尝试进行行和列的操作，那么有一些规则会很有用。这些规则描述如下

• 如果我们将行变成列，将列变成行，在这种情况下，行列式的值不会改变。
• 如果我们交换任意两行或两列，在这种情况下，行列式的符号会改变。
• 当且仅当任意两行或两列相同时，给定矩阵的行列式值为 0。
• 如果矩阵中有一个常数乘以该矩阵特定行或列的每个元素，在这种情况下，该常数也将乘以行列式的值。
• 如果行或列的每个元素都表示为元素之和的形式，在这种情况下，行列式也将表示为行列式之和的形式。
• 如果我们将一行或一列的元素加上或减去另一行或另一列元素的相应倍数，行列式的值不会改变。

关于行列式的重要说明

在学习行列式概念时，有一些要点我们应该记住。这些要点描述如下

• 我们可以将行列式视为一个函数。这意味着它可以将一个方阵作为输入，并返回一个单一的数字作为输出。
• 如果一个矩阵的行数和列数相同，那么它就被称为方阵。
• 如果有一个最简单的 1*1 阶方阵，那么该矩阵的行列式就是数字本身，因为 1*1 矩阵只包含一个数字。

行列式的例子

有很多行列式的例子，其中一些描述如下

示例 1：在这个例子中，我们有一个矩阵 A，我们必须确定这个矩阵的行列式。这个矩阵的元素描述如下

解：上述矩阵的行列式可以写成以下方式

现在我们将通过乘以对角线元素并减去其乘积来确定其行列式，如下所示

|A| = (4*2) - (3*1)

= 8 - 3

= 5

答案：det(A) 或 |A| = 5

示例 2：在这个例子中，我们有一个 2*2 阶的矩阵 C，我们必须确定这个矩阵的行列式。这个矩阵的元素描述如下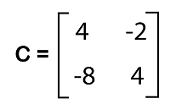

解：上述 2*2 矩阵的行列式可以写成以下方式

现在我们将按以下方式确定其行列式

|C| = {(4)(4) - (8)(2)}

= 16-16

= 0

答案：矩阵 C 的行列式 = 0。

示例 3：在这个例子中，我们有一个 3*3 阶的矩阵 A，我们必须确定这个矩阵的行列式。这个矩阵的元素描述如下

解：这里，我们将使用第一行展开上述 3*3 矩阵的行列式。

= 1 * (-1 - (-9) - 3 * (-3 - (-6) + 2 * (-9 - (-2))

= 1* (-1 + 9) - 3* (-3 + 6) + 2 * (-9 + 2)

= 8 - 9 - 14

= -15

答案：矩阵 A 的行列式是 -15。

示例 4：在这个例子中，我们必须借助行列式的性质来确定行列式的值。行列式描述如下

解：借助行列式的一个性质，我们将对上述行列式执行初等行变换 R₁ → R₁ + R₂ + R₃。根据这个性质，在进行初等行变换时，行列式的值不会改变。执行初等行变换 (R₁ → R₁ + R₂ + R₃) 后，行列式将变为以下形式

现在我们将使用另一个行列式性质，该性质表明如果矩阵的一行或一列为 0，那么该矩阵的行列式也将为 0。在上述矩阵中，第一行为 0。这就是为什么上述行列式的值为 0。

答案：行列式的值为 0。