离散数学中的色多项式

George Birkhoff 在 1912 年研究四色问题时，引入了色多项式概念。色多项式可以描述为一个函数，它借助颜色来找出图的适当着色数。色多项式的主要特性是它将证明四种颜色可以用来为每张地图着色。它们的着色方式是，共享边界的区域不应共享相同的颜色。色多项式也有许多有趣的特性。在本节中，我们将学习其中一些特性。

重要定义

为了理解这个概念，我们将学习一些定义，具体如下

1. 图 G 可以描述为边集和顶点集的集合。其中每条边连接两个顶点。如果两个顶点通过一条边连接，则称“这两个顶点相邻”。
2. 包含 v 个顶点的空图可以描述为包含 n 个顶点且没有边的图。包含 5 个顶点的空图如下所示
   
3. 图的阶数可以通过顶点数 n 确定。图的大小可以通过边数 m 确定。
4. 图 G 的连通分量可以定义为 G 的一个连通子图，该子图不与 G 中的任何其他顶点连接。
5. 图的适当着色可以描述为一种着色方式，其中相邻顶点不应使用相同的颜色。

我们将借助下图 G 来解释这些定义

在上述图 G 中，阶数 n = 9，大小 m = 8。

上述图 G 包含 3 个连通分量，可以用顶点集 {1, 2, 3}、{4, 5} 和 {6, 7, 8, 9} 表示。

对于 G 的适当着色，我们将使用一种颜色着色顶点集 {1, 3, 4, 6, 7}，使用第二种颜色着色顶点集 {2, 5, 9}，使用第三种颜色着色顶点集 {8}。在此过程中，我们不能使用相同的颜色着色与任何其他顶点共享边的顶点。

色多项式

图的色多项式可以描述为一个函数，它提供图 G 使用 x 种颜色进行适当着色的数量。我们可以借助删除收缩法来确定任何图的色多项式。

现在我们将通过一个简单的例子来解释色多项式这个概念。为此，我们将考虑一个图，描述如下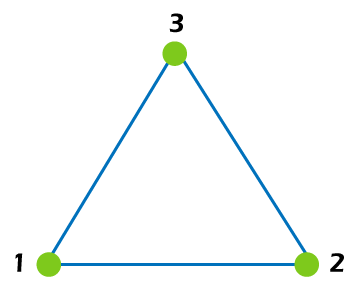

假设有 x 种颜色用于着色此图。我们可以使用以下方法系统地创建适当着色。

1. 顶点 1 是第一个着色顶点。对于此顶点，我们有 x 种颜色选择。
2. 下一个顶点是着色顶点 2。对于此顶点，我们只有 x-1 种选择。这是因为顶点 2 与顶点 1 相邻。
3. 下一个顶点是顶点 3，与顶点 1 和 2 相邻。因此，我们不能使用我们已经用于着色顶点 1 和顶点 2 的两种颜色。所以为了着色它，我们只有 x-2 种选择。

借助产生这种适当着色类型的方法，我们可以轻松找出用 x 种颜色着色此图的方式数量或色多项式，如下所示

然而，计算图的色多项式通常不是一个简单的过程。实际上，以最小化颜色数量的方式选择如何为图着色非常复杂。因此，我们需要一种更好的方法来持续获得图的色多项式。为此，可以使用删除收缩法。

计算色多项式

从以上描述中，我们了解到任何给定图的色多项式都可以通过删除收缩法确定。在此过程中，我们实际上在每个步骤中都在减少图。我们将通过更少的边和更少的顶点（在收缩的情况下）来完成此操作。当我们知道任何图的色多项式时，我们不需要继续对其进行删除收缩过程。

如果出现我们无法获取任何中间图的色多项式信息的情况，通过删除收缩法将生成一系列空图。如果我们有空图的色多项式信息，那么通过删除收缩法，我们将能够找到给定图的色多项式。

在学习色多项式时，我们还将了解到空图不会连接到多个顶点。因此，我们可以说我们可以根据其连通分量轻松确定不连通图的色多项式。