离散数学中的图论

图论可以被描述为对图的研究。图是一种数学结构，用于通过连接一组点来表示特定的函数。我们可以使用图来创建对象之间的成对关系。

图是由顶点和边构成的。顶点也称为节点，边也称为线。在任何图中，边都用于连接顶点。我们可以将线性图的应用不仅用于离散数学，还可以用于生物学、计算机科学、语言学、物理学、化学等领域。GPS（全球定位系统）是图结构的最佳现实生活示例，因为GPS用于跟踪路径或了解道路方向。

什么是图

图可以通过图形表示以有组织的方式显示任何数据。我们可以通过图显示变量量之间的关系。在图论中，我们通常使用图来表示一组对象，这些对象以某种方式相互连接。对象可以被描述为数学概念，可以用节点或顶点来表示，节点之间的关系可以用边来表示。

莱昂哈德·欧拉引入了图论的概念。他是一位非常著名的瑞士数学家。基于给定的点集或给定数据，他构建了图并解决了许多数学问题。他说，不同类型的数据可以通过图形表示以各种形式显示，例如折线图、柱状图、点图、饼图、频率表等。

图论的定义

图论可以被描述为对点和线的学习。图论是用于研究图的一个子领域。通过图形表示，我们能够显示数学真理。在图论的过程中，可以显示节点和边之间的关系。

形式上，图可以用 G(V, E) 对表示。

其中 V 用于表示有限顶点集，E 用于表示有限边集。

因此，图基本上包含非空边集 E 和顶点集 V。

例如： 假设有一个图 G = (V, E)，其中

V = {a, b, c, d}，并且

E = {(a, b), (a, c), (b, c), (c, d)}。

图的类型

图基本上有两种类型，即无向图和有向图。有向图和无向图描述如下：

有向图

有向图由一组顶点构成，这些顶点由有向边连接。在有向图中，边具有与顶点关联的方向。

在上图的有向图中，箭头用于显示方向。

无向图

无向图也可以由一组顶点构成，这些顶点通过无向边连接在一起。该图的所有边都是双向的。我们有时可以将这种图称为无向网络。

在无向图中，没有箭头。

其他类型的图

还有一些其他类型的图，描述如下：

零图（Null Graph）： 如果一个图不包含任何边，则称为零图。我们可以用符号 Nn 表示具有 n 个顶点的零图。零图的图示如下：

在上图中，顶点 a、b 和 c 没有通过任何边连接，也没有边。所以这是一个零图。

简单图（Simple Graph）： 如果一个图不包含任何类型的自环和多重边，则称为简单图。简单图必须是无向图。简单图的图示如下：

上图是无向图，不包含自环和多重边。所以这是一个简单图。

多重图（Multi-Graph）： 如果同一组顶点包含多重边，则称为多重图。在这种类型的图中，我们可以形成至少一个自环或一个以上的边。多重图的图示如下：

在上图中，顶点 a、b 和 c 包含多于一条边，并且不包含自环。所以这是一个多重图。

连通图（Connected Graph）： 如果一个图包含两个可以通过路径连接的顶点，则称为连通图。连通图的图示如下：

在上图中，两个顶点 a 和 b 通过单条路径连接。同样，其他顶点如（a 和 c）、（c 和 b）、（c 和 d）、（a 和 d）都通过单条路径连接。所以这是一个连通图。

不连通图（Disconnected Graph）： 如果一个图包含两个无法通过路径连接的顶点，则称为不连通图。如果有一个图 G 是不连通的，在这种情况下，G 的每个最大连通子图都将被称为图 G 的连通分量。不连通图的图示如下：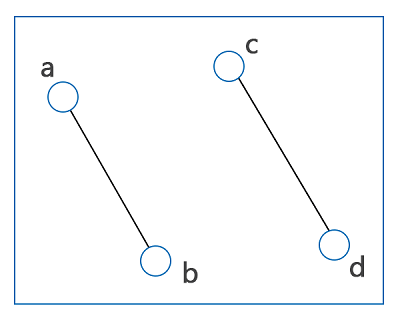

在上图中，顶点 a、c 和 b、d 之间无法通过路径连接。所以这是一个不连通图。

环图（Cycle Graph）： 如果一个图形成一个环，则称为环图。这意味着对于环图，给定的图必须有一个单一的环。我们可以用符号 Cn 表示具有 n 个顶点的环图。环图的图示如下：

上图通过路径 a、b、c 和 a 形成了一个环。所以这是一个环图。

完全图（Complete Graph）： 如果每对顶点都通过恰好一条边连接，则称为完全图。如果一个无向图有 n 个顶点，并且每对顶点之间恰好有一条边，则该图为完全图。我们可以用符号 Kn 表示具有 n 个顶点的完全图。在完全图中，具有 n 个顶点的边的总数为：

完全图的图示如下：

在上图中，两个顶点 a、c 通过单条边连接。同样，所有其他顶点（a 和 b）以及（c 和 b）都通过单条边连接。所以这是一个连通图。

平面图（Planer Graph）： 如果一个图可以在单个平面上绘制，并且该图的两条边不相交，则称为平面图。在该图中，所有节点和边都可以在平面上绘制。平面图的图示如下：

在上图中，没有边相互交叉，并且该图在一个平面内形成。所以这是一个平面图。

非平面图（Non-planer graph）： 如果一个图无法在一个平面上绘制，并且该图的两条边必须相互交叉，则该图称为非平面图。非平面图的图示如下：

在上图中，有许多边交叉，并且该图不形成在一个平面内。所以这是一个非平面图。

图的性质

• 根可以被描述为网络的起始点。
• 如果同类型的节点相互连接，则称该图为同质图（assortative graph）。在所有其他情况下，该图被称为异质图（disassortative graph）。
• 如果一个环图包含单个环，则该类型的环图将被称为一个图。
• 如果使用单条边连接所有顶点对，则该类型的图称为完全图。
• 如果每对顶点都以相同的方向或反方向连接，则该类型的图称为对称图（symmetry graph）。
• 如果有一个图只有一个图，则该类型的图将是一个路径图。

树、度、环等

在图表示中，我们可以使用一些术语，即树、度、环等。现在我们将详细学习它们。

树

树是一种无向网络图。树只有一条路径可以连接任意两个顶点。英国数学家亚瑟·凯莱于 1857 年引入了树的概念。树不能有自环和环。树的图示如下：

上图是一个无向图，只有一条路径连接两个顶点。所以这是一个树。

度

在任何图中，度都可以通过连接到顶点的边的数量来计算。符号 deg(v) 用于表示度，其中 v 用于表示图的顶点。因此，度基本上可以被描述为顶点的度量。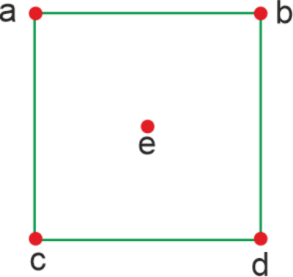

在上图中，共有 5 个顶点。顶点 a 的度为 2，顶点 b 的度为 2，顶点 c 的度为 2，顶点 d 的度为 2，顶点 e 的度为零。

环

在任何图中，环可以被描述为一个形成回路的闭合路径。如果图的起点和终点相同，并且包含一组顶点，则会在图中形成一个环。如果环不包含重复的顶点，则称为简单环。我们可以用符号 Cn 表示环图。环图可以分为两种类型：偶数环和奇数环。

• 偶数环（Even cycle）： 如果一个图的环包含偶数个节点和边，则该类型的环称为偶数环。
• 奇数环（Odd cycle）： 如果一个图的环包含奇数个节点和边，则该类型的环称为奇数环。

环的图示如下：

在上图中，所有图都形成了一个环，如果我们从任何顶点开始，都可以结束在同一个顶点。这意味着在上图中的所有图中，起点和终点都是相同的。所以这是一个环。

图 C3 和 C5 包含奇数个顶点和边，即 C3 包含 3 个顶点和边，图 C5 包含 5 个顶点和边。因此，图 C3 和 C5 包含奇数环。同样，图 C4 和 C6 包含偶数个顶点和边，即 C4 包含 4 个顶点和边，图 C6 包含 6 个顶点和边。因此，图 C4 和 C6 包含偶数环。

二分图

如果一个简单图包含两个独立的顶点集，则称为二分图。该图的顶点将以这样的方式连接：该图中的每条边都可以从第一个集连接到第二个集。这意味着第一个集合的顶点只能与第二个集合的顶点连接。同样，第二个集合的顶点也只能与第一个集合的顶点连接。但是，该图不包含任何可以连接同一集合内顶点的边。二分图的图示如下：

在上图中，我们有两个顶点集。集合 U 包含 5 个顶点，即 U1、U2、U3、U4、U5，集合 V 包含 4 个顶点，即 V1、V2、V3、V4。集合 U 的顶点仅与集合 V 的顶点有映射。同样，集合 V 的顶点与集合 U 的顶点有映射。集合 U 和集合 V 之间没有连接到同一组顶点的连接。所以这是一个二分图。

完全二分图

如果一个图包含两个集合，其中第一个集合的每个顶点都与第二个集合的每个顶点都有连接，则该图称为完全二分图。我们可以用符号 KX, Y 表示完全二分图。这意味着完全二分图的第一个集合包含 x 个顶点，第二个集合包含 y 个顶点。

在上图中，总共有两个集合。第一个集合包含 3 个顶点，第二个集合包含 4 个顶点。这意味着 x、y 的值将是 3、4。第一个集合的每个顶点都与第二个集合的每个顶点连接。所以这是一个完全二分图。

轮子

轮图（Wheel graph）和圈图（Cycle graph）都相似，但轮图有一个额外的顶点，它用于与所有其他顶点连接。我们可以用符号 Wn 表示具有 n 个顶点和 1 个额外顶点的轮图。在轮图中，具有 n 个顶点的边的总数为：

轮图的图示如下：

在上图中，我们有四个图 W3、W4、W5 和 W6。所有图都有一个额外的顶点，用于连接所有其他顶点。所以这些图是轮图。

超立方体

超立方体也可以称为 n-立方体。这个超立方体类似于三维立方体，但这种立方体可以有任意数量的维度。超立方体是一个紧凑、封闭、凸的几何图形，其中所有边都相互垂直且长度相等。该立方体包含 2n 个顶点，每个顶点由一个 n 位字符串表示。我们可以用符号 Qn 表示具有 2n 个顶点的超立方体。在立方体图中，具有 2n 个顶点的边的总数为：

超立方体的图示如下：

上图是紧凑且封闭的，并且该图的所有边都相互垂直且长度相等。所以这是一个超立方体。

图论算法

图的算法可以定义为计算任何函数的过程，或者绘制任何给定函数的图的过程。如果我们想用图解法解决问题，那么我们必须遵循预定义的步骤或指令集。图论遵循不同类型的算法，描述如下：

Ford-Fulkerson 算法

该算法是一种贪婪方法。在任何图或任何网络中，我们可以使用 Ford-Fulkerson 算法来计算可能的最大流量。该算法使用一个术语“流网络”，它可以用来表示具有源（S）和汇（T）的图的顶点和边。这里每条边都必须有一个容量。除了 S 和 T 之外，每个顶点都可以发送等量的东西。这是因为 S 只能发送，T 只能接收。我们可以通过以下约束来确定从 s 到 t 的最大可能流量：

1. 在任何图中，边的流量不应超过边的给定容量。
2. 除了 s 和 t 之外，每个顶点必须具有相等的输入流量和输出流量。

Bellman-Ford 算法

Bellman-Ford 算法可以被描述为一种单源最短路径算法。我们可以在带权图中对其进行使用，该算法将用于确定从选定顶点到所有其他顶点的最短路径。Dijkstra 算法和 Bellman-Ford 算法非常相似。主要区别在于 Bellman-Ford 算法能够处理负权边。这就是为什么 Bellman-Ford 算法如此受欢迎。

Edmonds-Karp 算法

该算法也称为最大流算法。该算法是 Ford-Fulkerson 算法的一种特定实现。Edmonds-Karp 算法和 Ford-Fulkerson 算法之间的主要区别在于，Ford-Fulkerson 算法包含一些未指定的协议部分，而 Edmonds-Karp 算法是完全指定的。Edmonds-Karp 算法中有不同类型的技术，可以用来确定增广路径。该算法用于处理与最大流最小割相关的问题。该算法还用于表明我们可以在程序的中间阶段使用广度优先搜索来确定最短距离。

Boruvka 算法

该算法用于在不同边权重图上确定最小生成树。在该算法中，图的边不包含相同的值。Boruvka 算法是 1926 年开发的第一个用于确定最小生成树（MST）的算法。该算法主要用于通过顶点之间的最短边连接顶点。