离散数学中的正交矩阵

如果一个矩阵的转置与其逆矩阵相似，则称该矩阵为正交矩阵。现在我们将学习矩阵的转置。如果交换了原矩阵的行或列的元素，则称该矩阵为转置矩阵。我们已经学过，如果原矩阵与其转置矩阵相似，则该矩阵称为对称矩阵。但在正交矩阵的情况下，矩阵的逆与其转置是相同的。在本节中，我们将学习正交矩阵、其定义、行列式、逆、性质、示例等。

什么是正交矩阵

如果有一个方阵，那么如果该矩阵的转置与其逆矩阵相似，则称该矩阵为正交矩阵，即 A^T = A^-1。其中 A^T 表示矩阵 A 的转置，A^-1 表示矩阵 A 的逆。根据其定义，还有一种正交矩阵的定义，如下所述：

A^T = A^-1

现在我们将上述等式两边同时乘以 A，如下所示：

AA^T = AA^-1

正如我们所学到的，AA^-1 = I，其中 I 表示单位矩阵，其阶数与矩阵 A 相同。

因此，AA^-1 = I。

同样，我们也可以证明 A^TA = I。

从上面的两个方程，我们将得到以下方程：

AA^T = A^TA = I。

因此，正交矩阵用于包含两个定义，它们将在正交矩阵的定义中显示。

正交矩阵的定义

正交矩阵有两种定义。根据第一个定义，如果矩阵的转置与矩阵的逆相似，则该矩阵称为正交矩阵。根据第二个定义，如果我们得到单位矩阵作为给定矩阵与其转置矩阵的乘积，则该给定矩阵称为正交矩阵。

假设有一个大小为 n*n 的方阵 A。如果该矩阵满足以下条件，则认为它是正交矩阵：

A^T = A^-1 (或)

AA^T = A^TA = I

注意

• 所有正交矩阵都必须是可逆的。转置保持行列式不变。这是因为我们可以说，在正交矩阵的情况下，行列式总是 +1 或 -1。
• 所有正交矩阵都必须是方阵，但并非所有方阵都是正交矩阵。

正交矩阵示例

在此示例中，我们有一个矩阵 A 及其转置矩阵 A^T。这里我们需要将给定矩阵与其转置矩阵相乘。给定矩阵的元素描述如下：

转置矩阵描述如下：

现在我们将按照以下方式相乘两个矩阵：

同样，我们也可以证明 AA^T = I。因此，矩阵 A 是一个 2*2 阶正交矩阵的示例。

如何找到正交矩阵

有一些步骤应该遵循，以确定矩阵是否为正交矩阵。为此，我们将假设一个方阵 A。这些步骤描述如下：

步骤 1：在此步骤中，我们将确定给定矩阵的行列式。如果该矩阵的行列式为 1，则矩阵 A 可能是正交矩阵。

步骤 2：在此步骤中，我们将确定该矩阵的转置和矩阵的逆。

步骤 3：如果矩阵 A 的转置与矩阵 A 的逆的乘积为单位矩阵，即 A^T * A^-1 = I，则该矩阵称为正交矩阵。否则，它不是正交矩阵。这里 I 表示单位矩阵。

正交矩阵的行列式

在正交矩阵的情况下，如果我们计算行列式，它总是 +1 或 -1。现在我们将证明它。为此，我们将假设一个正交矩阵 A。根据其定义，我们知道：

AA^T = I

现在我们将上述等式两边执行行列式运算，得到以下结果：

det(AA^T) = det(I)

我们已经了解到，如果我们计算单位矩阵的行列式，我们会得到 1。此外，如果存在两个矩阵 A 和 B，则 det(AB) = detA * detB。所以：

det(A) * det(A^T) = 1

我们已经知道 det(A) = det(A^T)。所以：

det(A) * det(A) = 1

[det(A)]² = 1

det(A) = ±1

正交矩阵的逆

根据正交矩阵的定义，我们知道对于任何正交矩阵 A，都有 A^-1 = A^T。现在我们将尝试通过这个定义以及另一个定义来证明它，即：

AA^T = A^TA = I ...... (1)

如果存在两个矩阵 A 和 B，那么如果它们满足以下条件，它们将互为逆矩阵：

AB = BA = I .... (2)

根据方程 (1) 和 (2)，我们可以看到 B = A^T。因为 B 是 A 的逆，所以 B = A^T 等同于 A^-1 = A^T。

因此，证明了正交矩阵的逆就是其转置。

正交矩阵的性质

基于其定义，正交矩阵有各种性质，其中一些描述如下：

• 正交矩阵的转置和逆与其相似，即 A^-1 = A^T。
• 如果我们相乘给定矩阵 A 和其转置矩阵，结果将得到一个单位矩阵，即 AA^T = A^TA = I。
• 如果对角矩阵的元素为 1 或 -1，则它总是正交的。例如：
  
• A^T 也是正交的。如果存在 A^-1 = A^T 的关系，在这种情况下，A^-1 也将是正交的。
• 特征向量将是正交的，A 的特征值为 ±1。
• 如果存在一个单位矩阵 (I)，那么它将是正交的，即 I.I = I.I = I。
• 正交矩阵本质上是对称的。
• 正交矩阵的行列式为 det(A) = ±1。该矩阵的行列式不为 0。因此，正交矩阵始终是非奇异的。

正交矩阵的应用

正交矩阵有各种应用或用途，其中一些描述如下：

• 我们可以利用正交矩阵进行多通道信号处理。
• 我们可以利用正交矩阵进行多元时间序列分析。
• 我们可以在线性代数的许多算法中使用此矩阵。
• 我们可以在 QR 分解中使用此矩阵。

关于正交矩阵的重要说明

在学习正交矩阵的概念时，我们应该了解一些要点。这些要点描述如下：

• 当且仅当给定矩阵是方阵时，该矩阵才是正交矩阵。
• 如果给定矩阵的逆与其转置矩阵相似，则该方阵称为正交。
• 如果存在正交矩阵 A，则给定矩阵 A 及其转置矩阵 A^T 互为逆矩阵。
• 如果我们计算正交矩阵的行列式，我们将得到 1 或 -1 作为结果。
• 所有单位矩阵都必须是正交矩阵。
• 在正交矩阵中，如果我们对任意两行或两列执行点积，我们将始终得到 0 作为结果。
• 正交矩阵的任何行或列中始终存在一个单位向量。

正交矩阵的例子

有很多正交矩阵的例子，其中一些描述如下：

示例 1：在此示例中，我们有一个矩阵 A，并且需要确定该矩阵是否为正交矩阵。矩阵 A 的元素描述如下：

解答：我们可以通过两种方法确定给定矩阵是否为正交矩阵。第一种方法是检查矩阵 A 的转置是否与其逆矩阵相似。第二种方法是检查给定矩阵与其转置矩阵的乘积是否为单位矩阵。所以这里我们将使用第二种方法。

从问题中，我们有一个矩阵 A，其中：

上述矩阵的转置描述如下：

现在我们将矩阵 A 及其转置矩阵 A 相乘，得到以下结果：

我们可以看到，结果是一个单位矩阵。

因此，矩阵 A 是一个正交矩阵。

示例 2：在此示例中，我们有一个 2*2 矩阵 A，需要确定它是否为正交矩阵。

解答：在正交矩阵的性质部分，我们已经了解到正交矩阵的行列式必须是 ±1。现在我们将按照以下方式计算矩阵 A 的行列式：

|A| = cos x * cos x - sin x * (-sin x)

|A| = cos² x + sin² x (根据三角学，我们知道 cos² x + sin² x = 1)

|A| = 1

矩阵 A 的行列式是 1。

因此，矩阵 A 是一个正交矩阵。

示例 3：在此示例中，我们有一个 3*3 矩阵 P。这里我们需要在不进行任何计算的情况下计算给定矩阵是否为正交矩阵。矩阵 P 的元素描述如下：

解答：给定矩阵 P 是一个对角矩阵，因为该矩阵的上三角元素和下三角元素除了主对角线元素外都等于 0。

当我们对矩阵 P 进行转置时，给定矩阵 P 及其转置矩阵将是相似的。

正如我们所知，如果给定矩阵与其转置矩阵相似，则该矩阵为对称矩阵。我们也知道，如果存在对称矩阵，则它将是正交矩阵。

因此，矩阵 P 是一个正交矩阵。

示例 4：在此示例中，我们有一个 3 阶正交矩阵 A。这里我们需要确定该正交矩阵的逆。该矩阵的元素描述如下：

解答：首先，我们将按以下方式确定给定矩阵的转置：

如果满足以下条件，我们将得到该矩阵的逆：

A * A^T = I

现在：

同样，我们也可以证明 A^T * A = I。

因此，证明了 A 是正交的。

那么 A^-1 = A^T，

答案：我们已经证明矩阵 A 是一个 3*3 阶正交矩阵，且 A^-1 =

示例 5：在此示例中，我们需要证明每个正交矩阵是否都是对称的。我们还需要用一个例子来证明我们的答案。

解答：如果矩阵 A 满足以下条件，则称为对称矩阵：

A = A^T

为此，我们将假设一个具有以下元素的正交矩阵 A：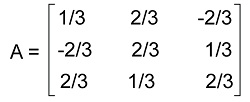

(我们可以通过证明 AA^T = A^TA = I 来证明该矩阵是正交的)。

现在我们将对假设的矩阵 A 进行转置，得到以下结果：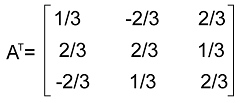

(我们可以证明 AA^T = A^TA = I)。

所以我们可以说，给定矩阵及其转置矩阵不相似，即：

A ≠ A^T

答案：并非所有正交矩阵都是对称的。

示例 6：在此示例中，我们有一个正交矩阵 A，并且需要确定 (AA^T)^-1。矩阵 A 的元素描述如下：

解答：从问题中，我们知道给定矩阵 A 是一个正交矩阵，即：

AA^T = I。

现在我们将上述等式两边同时加上逆运算，如下所示：

(AA^T)^-1 = I^-1。

正如我们所学到的，单位矩阵的逆就是它本身。所以：

I^-1 = I。

现在我们将这个代入上面的等式，得到以下结果：

(AA^T)^-1 = I

答案：(AA^T)^-1 = I，这是一个单位矩阵。

示例 7：在此示例中，我们有一个矩阵 A，需要确定它是否为正交矩阵。矩阵 A 的元素描述如下：

解答：在这里，我们将通过检查矩阵 A 的行列式来检查给定矩阵是否为正交矩阵。所以我们将看到给定矩阵的行列式是否等于 1。如果等于 1，则它是一个正交矩阵。

|A| = 4 * 9 - (-9) * 7

|A| = 36 + 63

|A| = 99 ≠ 1。

因此，矩阵 A 不是正交矩阵。