排列与组合

排列

将 n 个对象的集合按给定顺序排列称为对象的排列。将这些对象中任意 r ≤ n 个对象按给定顺序排列称为 r-排列或 n 个对象一次取 r 个对象的排列。

表示为 P (n, r)
                          P (n, r) =

定理： 证明 n 个事物全部取出的排列数为 n!。

证明： 我们知道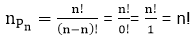

示例：4 x n_p3=n+1_P3

解： 4 x

               
                4 (n-2) = (n+1)
                 4n - 8 = n+1
                      3n = 9
                        n = 3.

带限制的排列

n 个不同对象一次取 r 个对象的排列数，其中 p 个特定对象不出现为

n 个不同对象一次取 r 个对象的排列数，其中 p 个特定对象存在为

示例： 如果每个数字都以“30”开头且没有数字重复，那么使用数字 0、1、2、3、4、5、6、7、8 可以组成多少个 6 位数字？

解： 所有数字都以“30”开头。因此，我们必须从剩余的 7 个数字中选择 4 个数字。

            ∴ 以“30”开头的数字总数为
7_P4 = =840。

带有重复对象的排列

定理： 证明当允许每个对象重复任意次数时，一次取出 n 个不同对象的不同排列数为 n^r。

证明： 假设我们有 n 个对象要填充 r 个位置，并且允许重复对象。

因此，填充第一个位置的方式的数量 = n
                 填充第二个位置的方式的数量 = n
                 .............................
                 .............................
                 填充第 r 个位置的方式的数量 = n
因此，用 n 个元素填充 r 个位置的总方式数为
                  = n. n. n..............r 次 =n^r。

循环排列

围绕一个圆进行的排列称为循环排列。

示例： 有多少种方法可以将字母 a、b、c、d、e、f、g、h、i、j 排列成一个圆？

解决方案 (10 - 1) = 9! = 362880

定理： 证明 n 个不同对象的循环排列数为 (n-1)!

证明： 让我们假设 K 是所需的排列数。

对于 K 的每个此类循环排列，都有 n 个相应的线性排列。如前所述，我们从循环排列中 n 个对象的每个对象开始。 因此，对于 K 个循环排列，我们有 K...n 个线性排列。

组合 (Combination)

组合是从一组给定对象中选择一些或所有对象，其中对象的顺序无关紧要。 n 个对象一次取 r 个对象的组合数表示为 n_Cr 或 C (n, r)。

证明： 一次取 r 个对象的 n 个不同事物的排列数由下式给出

由于对象的排列顺序无关紧要，因此，对于 r 个事物的每个组合，都有 r! 排列，即，

示例： 一位农民从拥有 6 头牛、5 头猪和 8 只母鸡的人那里购买了 3 头牛、2 头猪和 4 只母鸡。 找到农民拥有的选择数 m。

农民可以选择 C (6, 3) 种方式的牛，C (5, 2) 种方式的猪，C (8, 4) 种方式的母鸡。 因此，选择数 m 遵循