离散数学中的哈密顿图

如果一个连通图存在一个闭合的行走的轨迹，该轨迹遍历图中的所有顶点恰好一次，但起点或根顶点除外，那么这个图就称为哈密顿图。哈密顿行走不能重复任何边。哈密顿图的另一个定义是：如果一个连通图包含一个哈密顿回路，则该图称为哈密顿图。图中的顶点是相互连接的点集，这些线称为边。哈密顿图的例子如下所示。

• 在上面的图中，存在一个闭合的行走轨迹 ABCDEFA。
• 除了起点外，它遍历了图中所有顶点恰好一次。
• 在行走过程中，没有重复边。
• 基于以上所有原因，我们可以说这个图是哈密顿图。

换句话说，我们可以说上面的图包含一个哈密顿回路。因此，这个图是哈密顿图。

哈密顿路径

在一个连通图中，如果存在一条遍历图中所有顶点恰好一次的行走轨迹，则称这条轨迹为哈密顿路径。在这种行走轨迹中，边不能重复。还有一个定义可以描述哈密顿路径：如果一个连通图包含一条包含图中所有顶点的路径，则称这种路径为哈密顿路径。

哈密顿路径的例子

哈密顿路径有很多例子，如下所示。

示例 1： 在下图中，我们有 5 个节点。现在我们需要确定该图是否包含哈密顿路径。

解决方案

在上面的图中，我们可以看到，当我们从 A 开始，然后可以去 B、C、D，然后是 E。因此，这条路径恰好一次遍历了所有顶点（A、B、C、D 和 E），并且没有重复的边。因此，我们可以说该图具有哈密顿路径，如下所示。

哈密顿路径 = ABCDE

示例 2： 在下图中，我们有 5 个节点。现在我们需要确定该图是否包含哈密顿路径。

解决方案

在上面的图中，我们可以看到，当我们从 E 开始，然后可以去 A、B、C，然后是 D。因此，这条路径恰好一次遍历了所有顶点（A、B、C、D 和 E），并且没有重复的边。因此，我们可以说该图具有哈密顿路径，如下所示。

哈密顿路径 = EABCD

示例 3： 在下图中，我们有 5 个节点。现在我们需要确定该图是否包含哈密顿路径。

解决方案

在上面的图中，我们可以看到，没有一条路径可以一次遍历所有顶点（A、B、C、D 和 E）。如果我们从 F 开始，那么我们会去 A、B、C。在 C 之后，我们可以去 D 或 F，但我们不能同时去这两个顶点。因此，我们可以说这个图不包含哈密顿路径。

哈密顿回路

在一个连通图中，如果存在一条遍历图中所有顶点恰好一次的行走轨迹，并且在完成行走后返回到起始顶点，那么这种行走轨迹就称为哈密顿回路。对于哈密顿回路，不能有重复的边。我们也可以称哈密顿回路为哈密顿环。

还有一些关于哈密顿回路的定义，如下所示。

• 如果存在一条哈密顿路径，该路径始于某个顶点并终于同一顶点，则称这种环为哈密顿回路。
• 在连通图中，如果存在一个包含图中所有顶点的环，则称这种环为哈密顿回路。
• 封闭的哈密顿路径也称为哈密顿回路。

哈密顿回路的例子

哈密顿回路有很多例子，如下所示。

示例 1： 在下图中，我们有 5 个节点。现在我们需要确定该图是否包含哈密顿回路。

解决方案：=

当存在一条从某个顶点开始并回到同一顶点的路径时，上面的图就包含哈密顿回路。所以当我们从 A 开始，然后可以去 B、C、E、D，然后回到 A。因此，这条路径恰好一次遍历了所有顶点（A、B、C、D 和 E），但起点除外，并且没有重复的边。因此，我们可以说该图具有哈密顿回路，如下所示。

哈密顿回路 = ABCDEA

示例 2： 在下图中，我们有 5 个节点。现在我们需要确定该图是否包含哈密顿回路。

解决方案

当存在一条从某个顶点开始并回到同一顶点的路径时，上面的图就包含哈密顿回路。所以我们会从 E 开始，然后我们可以去 A、B、C、D。要回到同一个顶点 E，我们必须再次去顶点 A。因此，这条路径包含了所有顶点（A、B、C、D 和 E），但顶点 A 在回到起始顶点时被重复了。因此，我们可以说该图不包含哈密顿回路。

示例 3： 在下图中，我们有 6 个节点。现在我们需要确定该图是否包含哈密顿回路。

解决方案

当存在一条从某个顶点开始并回到同一顶点的路径时，上面的图就包含哈密顿回路。所以我们会从 F 开始，然后我们可以去 A、B、C、E。这条路径没有覆盖所有顶点（A、B、C、D、E 和 F）。因此，我们可以说该图不包含哈密顿回路。

重要提示

• 如果我们移除哈密顿路径的一条边，它就会变成一个哈密顿回路。
• 如果一个图有哈密顿回路，那么它也一定有哈密顿路径。但反过来则不一定成立。
• 一个图可以包含多个哈密顿路径和哈密顿回路。

哈密顿图的例子

哈密顿图有很多例子，如下所示。

示例 1： 在下图中，我们有 6 个节点。现在我们需要确定该图是否为哈密顿图。

解决方案

该图不包含哈密顿路径，因为当我们从 A 开始时，我们可以去顶点 B、C、D 和 E，但在此路径中，未覆盖顶点 F。该图也不包含哈密顿回路，因为当我们从 A 开始时，我们可以去顶点 B、C、D、E，然后回到 A。这可以形成一个回路，但在此路径中也未覆盖顶点 F。因此，我们可以说该图不包含哈密顿路径和哈密顿回路。因此，该图不是哈密顿图。

示例 2： 在下图中，我们有 5 个节点。现在我们需要确定该图是否为哈密顿图。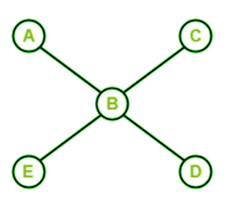

解决方案

该图不包含哈密顿路径，因为当我们从 A 和 B 开始时，我们可以去 C、D 和 E 三个地方中的一个。因此，这条路径没有覆盖所有顶点。该图也不包含哈密顿回路，因为任何路径都无法覆盖所有顶点并形成回路。因此，我们可以说该图不是哈密顿路径和哈密顿回路。因此，该图不是哈密顿图。

示例 3： 在下图中，我们有 7 个节点。现在我们需要确定该图是否为哈密顿图。

解决方案

该图包含哈密顿路径，因为当我们从 A 开始时，我们可以去顶点 B、C、D、E、F 和 G。该图也包含哈密顿回路，因为当我们从 A 开始时，我们可以去顶点 B、C、D、E、F、G，然后回到 A。因此，我们可以说该图包含哈密顿路径和哈密顿回路。哈密顿路径和哈密顿回路描述如下。

ABCDEFG 是上述图的哈密顿路径。

ABCDEFGA 是上述图的哈密顿回路。

因此，该图是哈密顿图。

示例 4： 在下图中，我们有 9 个节点。现在我们需要确定该图是否为哈密顿图。

解决方案

该图包含哈密顿路径，因为当我们从 A 开始时，我们可以去顶点 B、C、D、E、F、G、H 和 I。该图也包含哈密顿回路，因为当我们从 A 开始时，我们可以去顶点 B、C、D、E、F、G、H、I，然后回到 A。因此，我们可以说该图包含哈密顿路径和哈密顿回路。哈密顿路径和哈密顿回路描述如下。

ABCDEFGHI 是上述图的哈密顿路径。

ABCDEFGHIA 是上述图的哈密顿回路。

因此，该图是哈密顿图。

示例 5： 在下图中，我们有 5 个节点。现在我们需要确定该图是否为哈密顿图。

解决方案

该图不包含哈密顿路径，因为当我们从 A 开始时，我们可以去顶点 B、C 和 D，但在此路径中，未覆盖顶点 E。出于同样的原因，该图也不包含哈密顿回路。因此，我们可以说该图不是哈密顿路径和哈密顿回路。因此，该图不是哈密顿图。

示例 6： 在下图中，我们有 5 个节点。现在我们需要确定该图是否为哈密顿图。

解决方案

该图包含哈密顿路径，因为当我们从 A 开始时，我们可以去顶点 B、C、D 和 E。该图也包含哈密顿回路，因为当我们从 A 开始时，我们可以去顶点 B、C、D、E，然后回到 A。因此，我们可以说该图包含哈密顿路径和哈密顿回路。哈密顿路径和哈密顿回路描述如下。

ABCDE 是上述图的哈密顿路径。

ABCDEA 是上述图的哈密顿回路。

因此，该图是哈密顿图。