离散数学中的离散时间信号

如果信号只在离散的时间间隔内定义，则称为离散时间信号。我们可以用符号 x[n] 来表示离散时间信号，其中 n 表示时间域中的自变量。换句话说，我们可以使用数字信号来表示离散时间信号，如下所示：

这里 n 表示整数，x[n] 表示序列中的第 n 个样本。

通过对连续时间信号进行采样，我们通常可以得到离散时间信号。在这种情况下，序列的第 n 个样本和模拟信号 x_a(t) 在时间 t = nT 的值是相等的。

x[n] = xa(nT), -∞ < n < ∞

之后，**采样周期**将等于 T，采样频率将如下确定：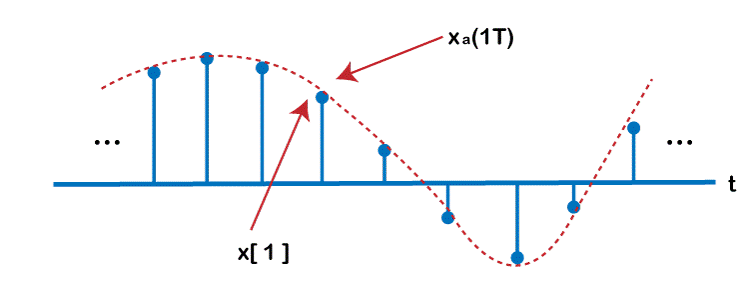

因此，尽管 x[n] 被严格称为序列中的第 n 个数字，但我们通常可以称它为第 n 个**样本**。当我们讨论整个序列时，它也可以被称为“序列 x[n]”。

在图形形式中，我们通常可以按以下方式描绘离散时间信号：

我们可以使用 MATLAB 函数 stem 来绘制离散时间信号。这里 x[n] 对于非整数 n 值是**未定义**的。

离散时间信号的表示

1. 图形表示
2. 函数表示
3. 表格表示
4. 序列表示

离散时间信号的图形表示

这里我们将假设一个离散时间信号 x(n) 具有一些值，如下所示：

x(0) = -1,

x(-1) = 0,

x(-2) = 3,

x(-3) = -2,

x(3) = 1,

x(2) = 3,

x(1) = 2

我们可以按以下方式图形化地表示离散时间信号：

离散时间信号的函数表示

在离散时间信号的函数表示中，信号的幅度将针对 n 的值进行书写。因此，我们可以通过函数表示像这样表示上面的离散时间信号 x(n)：

离散时间信号的表格表示

在离散时间信号的表格表示中，我们使用表格来表示采样时刻 n 以及离散时间信号在相应采样时刻的幅度。我们可以通过表格形式像这样表示上面的离散时间信号 x(n)：

离散时间信号的序列表示

在序列表示的形式中，我们可以按以下方式表示离散时间信号 x[n]：

其中

箭头符号 (↑) 用于指示对应于 n = 0 的项。如果序列表示不包含任何箭头，则该序列的第一项将对应于 n = 0。

离散时间序列的求和与乘积

通过将序列的相应元素相加，我们可以得到两个离散时间序列的和，如下所示：

通过将序列的相应元素相乘，我们可以得到两个离散时间序列的积，如下所示：

通过将序列的每个元素乘以一个常数，我们可以得到一个序列与常数 k 的积，如下所示：

{Cn} = k{an} → Cn = kan

我们可以通过多种方式来操作序列。我们可以通过逐点相加和逐点相乘来定义两个序列 x[n] 和 y[n] 的和与积。如果我们乘以 x[n] 的一个常数 a，这相当于将每个样本值乘以 a。

如果 y[n] 包含以下形式，则称 y[n] 是 x[n] 的**延迟**或**移位**版本：

Y[n] = x[n-n₀]

这里 n₀ 表示一个整数。

单位脉冲序列

单位脉冲序列可以定义如下：

单位脉冲序列的图形表示如下：

我们也可以将这种类型的序列称为**脉冲**或**离散时间脉冲**。狄拉克δ函数在离散时间信号和连续时间信号中的作用是相同的。因此，当我们定义离散时间信号时，不会造成任何复杂性，并且我们可以轻松地定义它们。

脉冲序列有一个重要的方面，即我们可以将任意序列表示为尺度化和延迟脉冲的总和。

例如：我们可以按以下方式表示序列：

x[n] = a_-4δ[n + 4] + a_-3δ[n + 3] + a_-2δ[n + 2] + a_-1δ[n + 1] + a₀δ[n] + a₁δ[n - 1] + a₂δ[n - 2] + a₃δ[n - 3] + a₄δ[n - 4]

一般来说，我们可以用以下方式来表示任何序列：

单位序列可以定义如下：

所示的单位序列的图形表示如下：

我们可以按以下方式将单位阶跃与脉冲联系起来：

还有另一种定义方式，如下所示：

反之，我们可以将单位脉冲序列表示为单位阶跃序列的第一个后向差分，如下所示：

指数序列

我们可以用**指数序列**来分析和表示离散时间系统。其一般形式如下：

x[n] = Aαn

如果存在两个实数 A 和 α，在这种情况下，序列将是实数。如果 A 为正且 0 < α < 1，在这种情况下，序列值将为正，并随着 n 的增加而减小，如下所示：

如果存在 -1 < α < 0 的情况，则序列的符号将交替出现，但幅度会减小。如果存在 |α| > 1 的情况，则 n 会增加，因此序列的幅度会增长。

**正弦序列**可以表示如下：

x[n] = A cos(w0n + φ) 对所有 n,

这里 A 和 φ 表示实常数。

正弦序列的图形表示如下：

我们可以按以下方式用复数 α = |α|e^jw0 和 A = |A|e^jφ 表示指数序列 Aαⁿ：

因此，实部和虚部用于表示指数加权的正弦波。

如果 |α| = 1，则序列将被称为复指数序列，如下所示：

x[n] = |A| ej(w0n + φ) = |A| cos (w0n + φ) + j |A| sin(w0n + φ)

因此，这个复指数正弦波具有 w₀ 频率，我们可以以每样本半径的形式来度量它。所以 φ 是信号的相位。

索引 n 始终表示一个整数。因此，在连续时间复指数和离散时间复指数的性质之间存在一些重要的差异，如下所示：

为此，我们将假设一个频率为 (w0 + 2π) 的复指数，如下所示：

x[n] = Aej(w0 + 2π)n = Aejw0n ej2π n = Aejw0n

因此，总而言之，我们可以说，具有频率 w₀ 的复指数序列和具有频率 (w₀+2π) 的复指数序列是完全相同的。更普遍地说，如果存在一个频率为 (w₀+2π) 的复指数序列，它与具有频率 w₀ 的序列是无法区分的，其中 r 表示一个整数。类似地，对于正弦序列，它将具有以下形式：

x[n] = A cos[(w0 + 2π r)n + φ] = A cos(w0n + φ)

在连续时间中，复指数序列和正弦序列总是周期性的。如果离散时间序列是周期性的，则它具有以下形式：

因此，离散时间正弦波只有在满足以下条件时才具有周期性：

A cos[(w0n + φ] = A cos(w0n + w0N + φ)

该序列需要满足以下条件：

如果我们想证明复指数序列 C e^jw0n 是周期性的，则需要满足相同的条件。

将上述两个因素结合起来，我们可以得出结论：只有 N 个可区分的频率，其对应的序列才具有周期 N。这种集合如下所示：

wk = 2π k/N, where k = 0, 1, 2, ...., N-1

此外，在离散时间序列的过程中，我们应该修改高频和低频的解释。如果存在一个离散时间正弦序列 x[n] = A cos[(w₀n + φ]，在这种情况下，随着 w₀ 从 0 增加到 π，它将振荡得更快；但在另一种情况下，随着它从 π 进一步增加到 2π，振荡会变慢。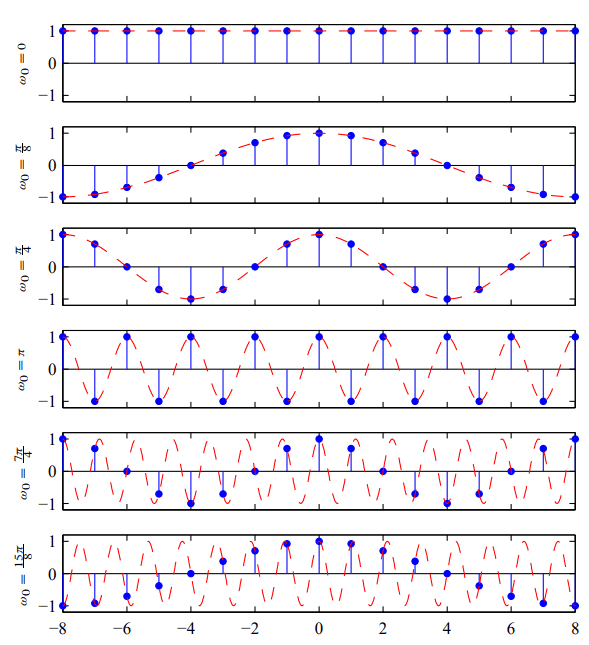

如果存在一个与 w₀ = 0 对应的序列，那么它将与 w₀ = 2π 的序列无法区分。总的来说，如果频率接近 w₀ = 2π k（其中 k 是整数），则这些频率被称为低频。在另一种情况下，如果频率接近 w₀ = (π + 2π k)，则这种频率被称为高频。

---

下一主题离散数学中的 M-array 树

← 上一篇 下一篇 →