柯西中值定理

柯西中值定理是对普通中值定理的推广。该定理也称为扩展中值定理或第二中值定理。普通中值定理描述的是，如果一个函数 f(x) 在闭区间 [a, b]（其中 a ≤ x ≤ b）上连续，在开区间 [a, b]（其中 a < x < b）上可导，那么在该区间上至少存在一点 x = c，满足

f(b) - f (a) = f' (c) (b-a)

它建立了两个函数导数与这些函数在有限区间上变化之间的关系。

让我们考虑函数 f(x) 和 g(x) 在区间 [a,b] 上连续，在 (a,b) 上可导，并且对于所有 x ε (a,b)，g'(x) ≠ 0。那么在该区间上存在一点 x = c，满足

柯西中值定理的证明

此处，柯西公式左侧的分母不为零：g(b)-g(a) ≠ 0。如果 g(b) = g(a)，根据罗尔定理，存在一点 d ∈ (a,b)，使得 g'(d) = 0。因此，这与假设 g'(x) ≠ 0 对于所有 x ∈ (a,b) 矛盾。

现在，我们应用辅助函数。

F (x) = f (x) + λg(x)

并选择 λ 以满足给定条件

F (a) = f (b)。我们得到，

f (a) + λg(a) = f (b) + λg(b)

= f(b)-f (a) = λ[g(a)- g(b)]

并且函数 F (x) 的形式为

函数 F (x) 在闭区间 (a ≤ x ≤ b) 上连续，在开区间 (a < x < b) 上可导，并且在区间的端点处取相同的值。因此，它满足罗尔定理的所有条件。那么，在区间 (a,b) 上存在一点 c，满足

F' (c) = 0。

由此可知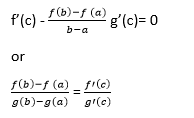

将 g (x) = x 代入给定公式，我们得到拉格朗日公式

柯西中值定理具有以下几何意义。考虑参数方程给出的曲线 ? X = f (t) 和 Y = g (t)，其中参数 t 位于区间 [a,b] 上。

当参数 t 变化时，曲线上点从 A (f (a). g(a) 移动到 B (f(b), g (b))。

根据柯西中值定理，曲线上存在一点 (f(c), g(c))，在该点处，曲线的切线平行于连接曲线的两个端点 A 和 B 的弦。

基于柯西中值定理的问题

问题 1

计算满足以下函数中值定理的 x 值

F(x) = x² + 2x + 2

说明

给定

f(x) = x² + 2x + 2

根据中值定理，

2c = -7

C = -7/2

问题2

计算满足以下函数中值定理的 x 值

F(x) = x² + 4x + 7

说明

给定

f(x) = x² + 4x + 7

根据中值定理，