如何找到色数 | 图的着色算法

要理解这个例子，我们需要了解上一篇文章，即 离散数学中的图的色数。

在色数一节中，我们学习了以下内容

• 图着色可以描述为为图的顶点分配颜色的过程。
• 在图着色中，两个相邻的顶点不能使用相同的颜色。
• 色数可以描述为正确着色任何图所需的最小颜色数。

图着色算法

• 如果我们想用最少的颜色数给图着色，为此没有高效的算法。
• 图着色也被称为 NP 完全算法。

但是，我们可以借助以下贪心算法找到图的色数。

贪婪算法

解决贪心算法有几个步骤，如下所述

步骤 1： 在第一步中，我们将第一个顶点着色为第一种颜色。

步骤 2： 现在，我们将逐一考虑所有剩余的顶点（V -1）并执行以下操作

• 只要当前选定的顶点的任何相邻顶点未使用相同的颜色，我们就用最小编号的颜色为当前选定的顶点着色。
• 如果其相邻顶点正在使用它，那么我们将选择下一个最小编号的颜色。
• 如果我们已经使用了所有之前的颜色，那么将使用一种新颜色来填充或分配给当前选定的顶点。

贪心算法的缺点

贪心算法有很多缺点，如下所述

• 在贪心算法中，不总是使用最少数量的颜色。
• 有时，颜色数量取决于处理顶点的顺序。

计算图的色数示例

有很多例子可以计算图的色数。其中一些如下所述

示例 1： 在此示例中，我们有一个图，并且需要确定该图的色数。

解决方案

当我们应用贪心算法时，我们将得到以下结果

从上表可以看出，

• 在上图中，我们需要最少 2 种颜色来给图着色。
• 因此，我们可以说上图的色数 = 2

所以，借助 2 种颜色，上图可以正确地着色如下

示例 2： 在此示例中，我们有一个图，并且需要确定该图的色数。

解决方案

当我们应用贪心算法时，我们将得到以下结果

从上表可以看出，

• 在上图中，我们需要最少 3 种颜色来给图着色。
• 因此，我们可以说上图的色数 = 3

所以，借助 3 种颜色，上图可以正确地着色如下

示例 3： 在此示例中，我们有一个图，并且需要确定该图的色数。

解决方案

当我们应用贪心算法时，我们将得到以下结果

从上表可以看出，

• 在上图中，我们需要最少 4 种颜色来给图着色。
• 因此，我们可以说上图的色数 = 4

所以，借助 4 种颜色，上图可以正确地着色如下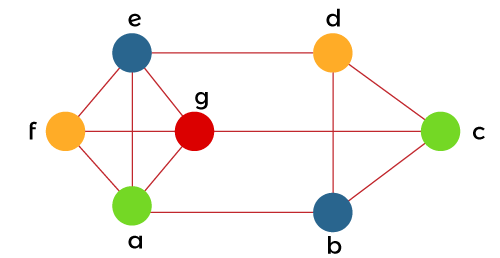

示例 4： 在此示例中，我们有一个图，并且需要确定该图的色数。

解决方案

当我们应用贪心算法时，我们将得到以下结果

从上表可以看出，

• 在上图中，我们需要最少 3 种颜色来给图着色。
• 因此，我们可以说上图的色数 = 3

所以，借助 3 种颜色，上图可以正确地着色如下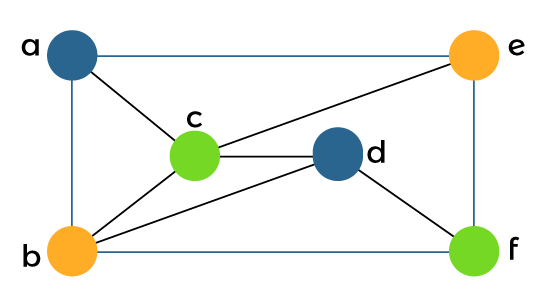

示例 5： 在此示例中，我们有一个图，并且需要确定该图的色数。

解决方案

当我们应用贪心算法时，我们将得到以下结果

• 在上图中，我们需要最少 3 种颜色来给图着色。
• 因此，我们可以说上图的色数 = 3

所以，借助 3 种颜色，上图可以正确地着色如下