Java Bellman-Ford 算法

2025 年 5 月 12 日 | 阅读 6 分钟

在动态规划中，有许多算法可以找到图中的最短路径。其中一些是Dijkstra 算法、BFS、DFS、Floyd、所有对最短路径问题和双向算法。最常用的算法是Dijkstra 算法。该算法的局限性在于，如果图具有负边权重，则无法应用。另一个区别是 Dijkstra 算法仅查看顶点的直接邻居，而 Bellman-Ford 在每次迭代中都遍历所有边。

为了克服这个问题，可以使用Bellman-Ford 算法。它可以处理负边权重。在本节中，我们将通过示例理解 Bellman-Ford 算法，并在 Java 程序中实现 Bellman ford 算法。

Bellman-Ford 算法

它是一种单源最短路径（最小权重）算法，与 Dijkstra 算法非常相似。如果我们想找到最短路径，就可以在图上应用它。请注意，它可以处理负边权重。该算法的局限性在于图中不应存在负环（边权之和为负值的环）。考虑以下带环图。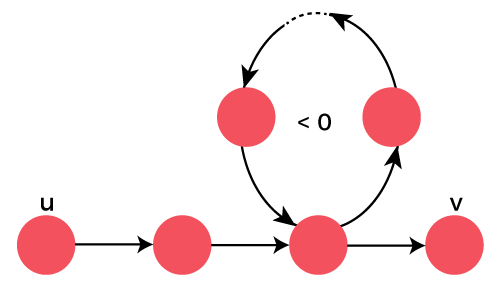

该算法的运行时复杂度为O(v*e)，空间复杂度为O(v)。如果图具有负边权重，则应使用该算法。因此，Bellman-Ford 算法可应用于以下情况：

负边权重
正边权重 > 1
无向环

当所有弧都是负数时，该算法比 Dijkstra 算法慢。

Bellman-Ford 算法的工作原理

Bellman-Ford 算法的工作原理与 Dijkstra 算法相同。唯一的区别是它不使用优先队列。它会重复遍历所有边，并像 Dijkstra 算法一样更新起点上的距离。

如果图G=(V, E)包含负权重环，则某些最短路径可能不存在。Bellman-Ford 算法找到从源s ϵ V到所有v ϵ V的所有最短路径长度，或确定存在负权重环。

给定一个有权重的有向图 G(V, E) 和源 (s) 以及权重函数w: E -> R，当且仅当图中不存在从源可达的负权重环时，该算法返回布尔值TRUE。该算法会产生最短路径及其权重。如果存在这样的环，则算法会指示无解。

算法

INITIALIZE-SINGLE-SOURCE (G, s)
for i <- 1 to |V[G]|-1
do for each edge (U, V) ϵ E[G]
do RELEAX (U, V, W)
for each edge (U, V) ϵ E[G]
do if d[V] > d[U] + w (U, V)
then return FALSE
return TRUE

Bellman Ford 伪代码

BellamanFord (G, V, E, S)
Step 1:
for each vertex v ϵ G do
dist[v] = ∞
dist[source] = 0

Step 2:
Relax (u, v, w)
for i = 1 to |v|-1
           for each edge (u, v) ϵ G do
           (dist[v] > dist[u]+w(u, v))
           (dist[v] <- dist[u]+w(u, v))
Step 3:
for each edge (u, v) ϵ G
if (dist[u]+w(u, v)< dist[v])
return "Graph contains negative weight cycle"
return distance

复杂度

时间复杂度	最佳情况	O(E)
	平均情况	O(VE)
	最坏情况	O(VE)
空间复杂度		O(V)

让我们通过一个例子来理解这个算法。

Bellman-Ford 示例

考虑以下有向图 (G)。

边的顺序：(B, E), (D, B), (B, D), (A, B), (A, C), (D, C), (B, C), (E, D)

在上图中 (G)，A 是所有其他顶点的起始顶点。

为了找到最短路径，首先，我们将源顶点 (A) 初始化为 0，将其他顶点初始化为无穷大 (∞)。之后，我们将从源节点遍历到每个顶点。在遍历过程中更新节点的值。我们创建了以下表格来更新距离。

从源顶点 A，我们可以到达顶点 B 和 C。

更新距离后，我们得到以下图。

从顶点 B，我们可以到达顶点 C、D 和 E。计算从 B 到其他顶点的距离，我们得到

更新距离后，我们得到以下图。

从顶点 C 无法移动到任何顶点，所以我们将访问下一个顶点，即 D。

从顶点 D，我们可以到达顶点 B 和 C。计算从顶点 D 到其他顶点的距离。

移动 D -> B，我们注意到顶点 B 已经有了最小距离，所以这次我们不会更新距离。

移动 D-> C，我们注意到顶点 C 已经有了最小距离，所以这次我们不会更新距离。

更新距离后，我们得到以下图。

从顶点 E，我们只能移动到顶点 D。计算从顶点 E 到 D 的距离。

更新距离后，我们得到以下图。

我们注意到值单调递减。

Java 中的 Bellman-Ford 实现

BellmanFordExample1.java

import java.util.ArrayList;
import java.util.List;
class Graph 
{
//vertices of the graph
private int V;  
//edges in the graph
private List<Edge> edges; 
//creating a constructor of the Graph class and generating getters and setters
public Graph(int v) 
{
V = v;
edges = new ArrayList<Edge>();
}
public int getV() 
{
return V;
}
public void setV(int v) 
{
V = v;
}
public List<Edge> getEdges() 
{
return edges;
}
public void setEdges(List<Edge> edges) 
{
this.edges = edges;
}
public void addEdge(int u, int v, int w) 
{
Edge e = new Edge(u, v, w);
edges.add(e);
}
}
class Edge 
{
//it is the source vertex    
private int u; 
//it is the destination vertex
private int v; 
//it denotes the weight on edge
private int w; 
//generating getters and setters
public int getU() 
{
return u;
}
public void setU(int u) 
{
this.u = u;
}
public int getV() 
{
return v;
}
public void setV(int v) 
{
this.v = v;
}
public int getW() 
{
return w;
}
public void setW(int w) 
{
this.w = w;
}
//creating constructor of the Edge class
public Edge(int u, int v, int w) 
{
this.u = u;
this.v = v;
this.w = w;
}
}
public class BellmanFordImplementation
{
public static void main(String args[]) 
{
Graph g = createGraph();
int distance[] = new int[g.getV()];
boolean hasNegativeCycle = getShortestPaths(g, 1, distance);
if(!hasNegativeCycle) 
{
System.out.println("Vertex \t: Distance");    
for(int i = 1; i < distance.length; i++)
System.out.println("\t"+i + " " + "\t\t"+(distance[i] == Integer.MAX_VALUE ? "-" : distance[i]));
} 
else 
{
System.out.println("Negative cycle exists in the graph, no solution found!!!");
}
}
private static Graph createGraph() 
{
int v = 7;
//creating a graph having 7 vertices
Graph g = new Graph(v);
//adding edges to the graph
g.addEdge(1, 2, 4);
g.addEdge(1, 4, 9);
g.addEdge(2, 3, -1);
g.addEdge(3, 6, 3);
g.addEdge(4, 3, 2);
g.addEdge(4, 5, -5);
g.addEdge(5, 6, 0);     
//returns graph
return g;
}
//Bellman-Ford logic
public static boolean getShortestPaths(Graph g, int source, int[] distance) 
{
int V = g.getV();
//initializing distances from source to other vertices
for(int i = 1; i < V; i++) 
{
distance[i] = Integer.MAX_VALUE;
}
//source vertex initialize to 0
distance[source] = 0;
//relaxing edges
for(int i = 1; i < V; i++) 
{
//iterate over edges    
for(Edge e: g.getEdges()) 
{
int u = e.getU(), v = e.getV(), w = e.getW();
if(distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + w) 
{
//calculates distance    
distance[v] = distance[u] + w;
}
}
}
//checks if there exist negative cycles in graph G
for(Edge e: g.getEdges()) 
{
int u = e.getU(), v = e.getV(), w = e.getW();
if(distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + w) 
{
return true;
}
}
return false;
}
}

输出

结论

找到具有非负边权重的图的最短路径是一个NP 难问题。要解决此类问题，不存在多项式时间算法。考虑一种情况，其中每条边都具有负边权重，我们可以应用 Bellman-Ford 算法。

可能存在从源可达的负权重环。在这种情况下，算法将终止。同样，如果我们想找到从源 (s) 到顶点 (v) 的最长简单路径，并且图中存在负环，则我们不能应用 Bellman-Ford 算法。

下一个主题zigzag-grid-traversal-with-skip-in-java

← 上一个下一个 →

Java Bellman-Ford 算法

Bellman-Ford 算法

Bellman-Ford 算法的工作原理

算法

Bellman Ford 伪代码

复杂度

Bellman-Ford 示例

Java 中的 Bellman-Ford 实现

结论

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

Java Conversion

Java Misc

Java Bellman-Ford 算法

Bellman-Ford 算法

Bellman-Ford 算法的工作原理

算法

Bellman Ford 伪代码

复杂度

Bellman-Ford 示例

Java 中的 Bellman-Ford 实现

结论

相关帖子

如何在 Java 中计算两个日期之间的时间差

Java 中的 Frame 类

AWS SDK for Java with Apache Maven

Java 练习程序

native Keyword in Java

Java 中的 Finalizer 链

Java 中 next() 和 nextLine() 方法的区别

Oracle Java

Java callback function

DecimalStyle getDecimalSeparator() method in Java with Examples

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器