Knapsack Problem Java

2025年5月7日 | 阅读7分钟

最显著的组合优化问题之一是背包问题 Java。背包问题有两种类别。

0-1 背包问题
分数背包问题

让我们来讨论一下它们。

0 - 1 背包问题

给定 n 个不同物品的价值和重量。需要将这些物品放入容量为 C 的背包中，使得背包的价值最大。同时，背包中所有物品的总重量不得超过容量 C。由于这是 0-1 背包问题；因此，不允许分割物品，即永远不能打碎任何给定的物品，要么不选它，要么选它（0-1 属性）。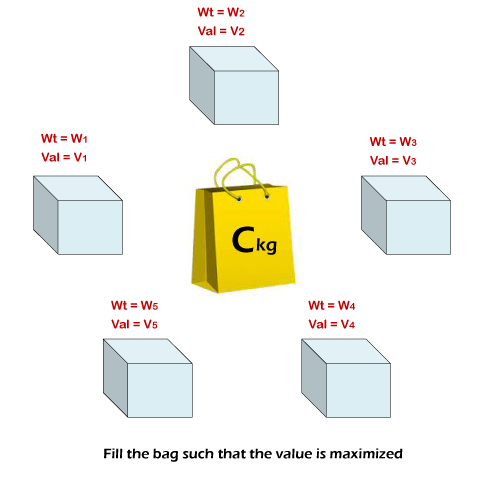

背包问题可以通过穷举搜索或动态规划来解决。

使用穷举搜索

穷举搜索意味着应用暴力方法。在此方法中，尝试所有物品的组合，并为每种组合计算价值。生成最大价值的组合就是答案。

以下程序使用递归实现暴力方法。

文件名： KnapsackExample.java

// A recursive implementation
// of the 0 - 1 Knapsack problem 
public class KnapsackExample
{
// A utility method, which returns
// the maximum of the two numbers a1 and a2
public int max(int a1, int a2)
{
return (a1 > a2) ? a1 : a2;
}
// A method that returns the maximum value that
// may be put in the given knapsack of
// capacity c by applying brute force with the help of recursion
public int maxknapSackVal(int C, int wt[], int v[], int l)
{
// handling Base Case
if (l == 0 || C == 0)
{
    // if no item is present or 
    // the capacity of the knapsack is 0, 
    // then there is no need to go further. 
    return 0;
}
// The capacity C of the knapsack is less 
// than the lth item. Therefore, it is 
// not possible to include this item 
// in creating the solution
if (wt[l - 1] > C)
{
return maxknapSackVal(C, wt, v, l - 1);
}
else
{
// recursively solving the answer
// Case 1: include the lth item
int val1 = maxknapSackVal(C - wt[l - 1], wt, v, l - 1);
// Case 2: exclude the lth item
int val2 = maxknapSackVal(C, wt, v, l - 1);
// return the maximum of both 
return max(v[l - 1] + val1, val2);
}
}
// main method
public static void main(String argvs[])
{
// input arrays
int values[] = new int[] { 100, 60, 120 };
int weight[] = new int[] { 20, 10, 30 };
// capacity of the knapsack
int C = 50;
// calculating the length
int length = values.length;
// instantiating the class KnapsackExample
KnapsackExample knapObj = new KnapsackExample();
int maxVal = knapObj.maxknapSackVal(C, weight, values, length);
System.out.println("The maximum value is: " + maxVal);
}
}

输出

The maximum value is: 220

解释：输入数组的映射方式是，对于物品 i，重量为 weight[i]，其价值为 values[i]。在每次递归调用中，都会做出一个决定，该物品是否应包含在解决方案中。如果不包含该物品，我们将继续进行，而不考虑其价值。如果包含该物品，则背包的容量会减少该物品的重量，我们继续进行，并包含其价值。其他物品也以类似的方式处理。通过添加所包含物品的价值产生的最大价值就是我们的答案。

请注意，该方法不是很方便，因为它需要很长时间才能给出结果。该方法的时空复杂度为 O(2 ^ n)，其中 n 是存在的元素数。

使用动态规划

之所以需要动态规划，是因为上述方法花费了大量时间来生成结果。因此，从长远来看，上述方法会失败。因此，我们需要寻找另一种方法，即动态规划。

文件名： KnapsackExample1.java

// A solution for the 0 - 1 Knapsack problem
// using dynamic programming
public class KnapsackExample1
{
// A utility method, which returns
// the maximum of two integers a1 and a2
public int maximum(int a1, int a2)
{
	return (a1 > a2) ? a1 : a2;
}
// Returns the maximum value that can
// be put in a knapsack of capacity C
public int maxValueKnapsack(int C, int w[], int val[], int l)
{
int j, wt;
int dp[][] = new int[l + 1][C + 1];
// Filling the table dp[][] in the bottom-up manner
for (j = 0; j <= l; j++)
{
for (wt = 0; wt <= C; wt++)
{
if (j == 0 || wt == 0)
{
    // base case
	dp[j][wt] = 0;
}
else if (w[j - 1] <= wt)
{
    // similar the previous approach making two choices 
    // either exluding or including the items
    dp[j][wt] = maximum(val[j - 1] + dp[j - 1][wt - w[j - 1]], dp[j - 1][wt]);
}
else
{
    // current capacity of the knapsack does not allow 
    // this item. The current value is equal to the previous value
    dp[j][wt] = dp[j - 1][wt];
}
}
}
return dp[j - 1][C];
}
//  main method
public static void main(String argvs[])
{
// input arrays
int values[] = new int[] { 100, 60, 120 };
int weight[] = new int[] { 20, 10, 30 };
// capacity of the knapsack
int C = 50;
// length of the input arrays
int l = values.length;
// instantiating the class KnapsackExample
KnapsackExample knapObj = new KnapsackExample();
// invoking the method maxValueKnapsack()
int maxVal = knapObj.maxValueKnapsack(C, weight, values, l);
// displaying the final result
System.out.println("The maximum value is: " + maxVal);
}
}

输出

The maximum value is: 220

解释：与第一种方法类似，这次我们也在包含和排除列表中的每个物品。然而，这次我们有 O(n^2) 的更好时空复杂度。这是因为，与上述方法不同，我们利用较小物品列表的解决方案来构建完整物品列表的解决方案（动态规划的属性）。因此，迭代次数较少。请注意，在两种方法中，我们完全排除了或包含了物品，从而遵循了 0-1 属性。

分数背包问题

分数背包问题与 0-1 背包问题类似。唯一的区别是可以部分选择一个物品。因此，给予了打破任何物品然后将其放入背包的自由，以便最大化背包中所有物品（无论是否打破）的总价值。

文件名： KnapsackExample1.java

// Java program to solve fractional Knapsack Problem
import java.util.Comparator;
import java.util.Arrays;
// the greedy approach
public class FractionalKnapSackExample
{
// method to get maximum value
private static double getMaxValue(int[] w, int[] v, int c)
{
// length of the array
int size = w.length;
// array of storing all the items
ItemValues[] iValue = new ItemValues[size];
for (int j = 0; j < size; j++) 
{
// storing the items
iValue[j] = new ItemValues(w[j], v[j], j);
}
// sorting the items on the basis of cost
Arrays.sort(iValue, new Comparator<ItemValues>() 
{
@Override
public int compare(ItemValues i1, ItemValues i2)
{
return i2.cost.compareTo(i1.cost);
}
});
// contains the maximum value that is possible 
// for the given capacity of the knapsack
double totalVal = 0d;
for (int j = 0; j < size; j++) 
{
// obtaining the current weight 
// and value of the ith item
int currWt = (int)iValue[j].w;
int currVal = (int)iValue[j].value;
if (c - currWt >= 0) 
{
// the current capacity of the knapsack allows the 
// item to be taken as a whole
c = c - currWt;
totalVal = totalVal + currVal;
}
else 
{
// when an item can not be picked as a whole
// we break the item and take a portion of it 
// such that we get the maximum value in the knapsack
double fraction	= ((double)c / (double)currWt);
totalVal = totalVal + (currVal * fraction);
c = (int)(c - (currWt * fraction));
// the knapsack is full 
// no need to proceed further
break;
}
}
return totalVal;
}
// Itemvalues class
static class ItemValues 
{
Double cost;
double w, value, index;
// item value function
public ItemValues(int w, int value, int index)
{
this.w = w;
this.value = value;
this.index = index;
// on the basis of cost 
// we sort the item
cost = new Double((double)value / (double)w);
}
}
// main method
public static void main(String argvs[])
{
// input arrays
int[] weight = { 40, 10, 20, 30 };
int[] values = { 40, 60, 100, 120 };
// capacity of the knapsack
int C = 50;
// invoking the getMaxValue() method        
double maxVal = getMaxValue(weight, values, C);
// printing the result
System.out.println("Maximum value that can be obtained is = " + maxVal);
}
}

输出

Maximum value that can be obtained is = 240.0

解释：贪心算法用于解决分数背包问题。在此方法中，我们首先考虑那些在消耗较少重量的同时能产生最大价值的物品。换句话说，那些价值/重量比最大的物品。因此，我们通过价值/重量比来对列表进行非递减排序。因此，价值/重量比最高的物品位于第一个索引，价值/重量比第二高的物品占据第二个索引，依此类推。

下一主题使用费马小定理在 Java 中计算 nCr 和 nPr

Knapsack Problem Java

0 - 1 背包问题

使用穷举搜索

使用动态规划

分数背包问题

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

Java Conversion

Java Misc

Knapsack Problem Java

0 - 1 背包问题

使用穷举搜索

使用动态规划

分数背包问题

相关帖子

Final Vs. Immutability in Java

Java 中检查两个给定矩阵是否互为镜像

Java 9 中 orTimeout() 和 completeOnTimeOut() 方法的区别

Java Editors

Java ArrayList 长度

List vs ArrayList

Java 控制台错误

Java ObjectInputStream Class

Java 中的荷兰国旗问题

Java 中的选择语句

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器