Mirror of n-ary Tree in Java

N 叉树的镜像是一种转换，其中每个节点的左右子树都被交换。这个概念类似于二叉树的镜像，但在这里，每个节点可以有多个子节点。要获得 N 叉树的镜像，我们需要递归地反转树中每个节点的子节点顺序。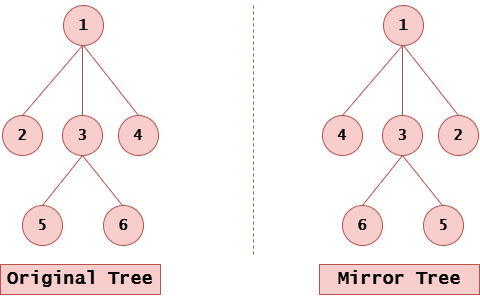

问题陈述

给定两个 N 叉树，我们需要检查它们是否互为镜像。如果它们是镜像，则打印是，否则打印否。

我们还给定e，表示两棵树的边数。两个数组A[]和B[]。每个数组都有 2*e 个空格分隔的值 u, v，表示两棵树中从 u 到 v 的一条边。

过程包括：

• 递归遍历树。
• 交换每个节点的子节点。
• 镜像树的所有子树。

这种变换对于各种树操作都很有用，包括某些搜索算法、模式匹配和可视化。镜像树保留了结构，但子节点顺序相反。

在继续本节之前，我们将首先找到如何找到 N 叉树的镜像树。

查找镜像树

在这种方法中，我们基本上通过后序遍历的方式反转 N 叉树。该算法类似于如何为二叉树创建镜像树。

在上面的函数convertToMirror(TreeNode root) 中，我们首先将所有以子节点为根的子树转换为它们的镜像（通过递归调用），然后反转子节点本身。

算法

步骤 1：通过创建节点并连接父子关系来构建 N 叉树。

步骤 2：递归遍历树以处理每个节点及其子树。

步骤 3：反转每个节点的子节点以创建镜像。

步骤 4：执行层序遍历以逐层打印树。

步骤 5：打印镜像前后的树结构。

输出

 
Original tree traversal:
 Level-0: 1 
 Level-1: 2 3 4 
 Level-2: 5 6 7 8 9 

Mirror tree traversal:
 Level-0: 1 
 Level-1: 4 3 2 
 Level-2: 9 8 7 6 5    

时间复杂度：O(N)，其中 N 是节点数。

辅助空间复杂度：O(1)，由于递归和用于层序遍历的队列。

检查两个 N 叉树是否为镜像

有两种方法可以解决此问题。

使用哈希

这种方法的基本思想是使用堆栈的无序映射来查看给定的 N 叉树是否互为镜像。

假设第一个 N 叉树是 t1，第二个 N 叉树是 t2。对于 t1 中的所有节点，将其相邻节点推入堆栈。现在，对于 t2 中的每个节点，如果其连接的节点与堆栈的顶部匹配，则从堆栈中弹出这些元素。

如果不匹配，如果堆栈的顶部与节点不匹配，则两棵树永远不会形成镜像。

然后对每个对应的节点重复此操作。

1. 遍历堆栈的映射。
   对于第一棵树的每个节点，将所有连接的节点推入堆栈的映射中。
2. 对于第二棵树的每个节点，再次遍历映射。

例如

现在让我们考虑第二棵树中的一个节点，例如 X。

对于节点 X，在映射中查看使用了哪个堆栈。

a = 第二棵树中节点 X 的堆栈顶部；

b = 第二棵树中 X 的连接节点。

if (a!= b)

return false;

从堆栈中弹出节点 X。

让我们在 Java 程序中实现上述方法。

输出

 
The trees are mirror: true   

解释

节点类：定义一个类来表示 N 叉树中的节点，每个节点存储数据和子节点列表。

1. areMirror 函数：通过以下方式检查两个 N 叉树是否为镜像：
   
   • 验证两棵树是否都为空（它们是镜像）。
   • 比较根值并确保它们相同。
   • 确保两棵树具有相同数量的子节点。
   • 递归地比较一棵树的每个子节点与另一棵树中对应的镜像子节点。
2. 主方法：创建两个示例 N 叉树，并使用 areMirror 函数检查它们是否为镜像。它打印结果，指示树是否为镜像。

本质上，该代码通过比较两个 N 叉树在对应位置的结构和值来验证它们是否互为镜像。