Figurate Number in Java

形数是数字序列的经典来源。在本节中，我们将学习什么是形数，并创建Java 程序来检查给定的数字是否为形数。形数程序经常出现在 Java 编码面试和学术中。

形数或几何数具有丰富的历史和许多应用。一般来说，形数是可以由具有等距点的规则离散几何图案表示的数字。如果点的排列形成一个规则多边形，则该数字分别称为多边形数。下表描述了形数及其序列。

形数也可以构成其他几何形状，例如中心多边形、L 形、三维（和多维）实体等。

形数

当圆上 n 个一般位置的点由直线连接时，形成的三角形（所有顶点都位于圆内）的数量。

形数，也称为几何数。它是可以用等距点的规则几何排列来表示的数字。如果排列形成规则多边形，则该数字称为多边形数。下表描述了形数及其序列。

让我们看一下形数的图形表示。下图说明了这一点。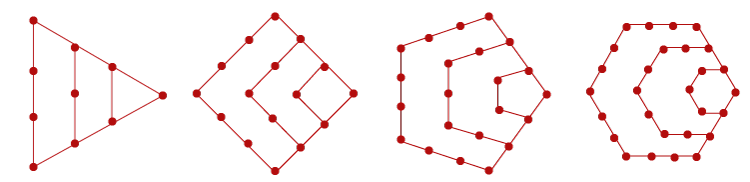

上面所示的多边形数分别称为三角形数、平方数、五边形数和六边形数。

它基于一个 6 维规则单形。它是 OEIS 序列A000579。它也称为二项式系数C(n, 6)。

根据Hyun Kwang Kim的说法，似乎每个非负整数都可以表示为g = 13个此类数字的总和。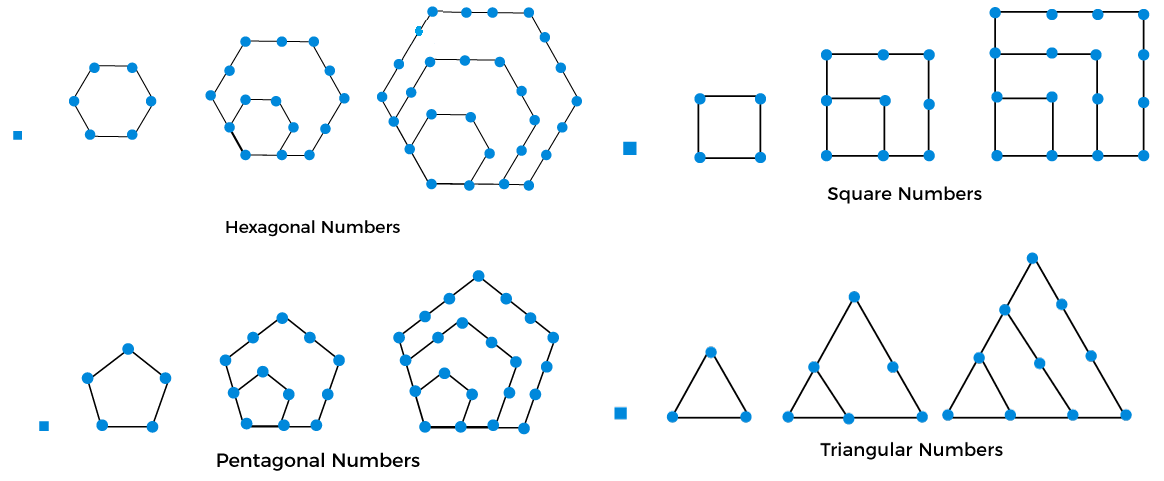

性质

• a(n) 是 (a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7)^n 展开式中的项数。该序列中唯一的素数是 7。
• 6 维三角形数，二项式变换 [1, 0, 0, 0, ...] 的第六个部分和。
• a(n) = fallfac(n, 6)/6! 也是秩为 6 且维度 n >= 1 的反对称张量的独立分量数。这里，fallfac 是下降阶乘。
• 作为无穷范数 n 的表示整格点的轨道的函数，当轨道基数等于 645120 时，Aut(Z^7) 的轨道数。
• 对于整数集 {1,2,...,n}，a(n) 是每个包含 5 个元素的子集的前 2 个最小元素之和，即 3*C(n+1,6)（对于 n>=5），因此 a(n) = 3*C(n+1,6) = 3*A000579(n+1)。
• a(n) = A000292(n-5)*A000292(n-2)/20

计算形数的公式

• 一般公式： x^6/(1-x)^7
• 指数公式： exp(x)*x^6/720
• 猜想： a(n+3) = Sum{0 <= k, l, m <= n; k + l + m <= n} k*l*m

其他一些公式是

• a(n) = (n^6 - 15*n^5 + 85*n^4 - 225*n^3 + 274*n^2 - 120*n)/720。
• a(n) = 3*C(n+1, 6)

上述公式引出了一个关于一般 N 边形数的猜想公式

注意：上述公式仅适用于 N=2、3 和 4。

形数示例

例如，考虑一个整数集Z = {1, 2, 3, 4, 5, 6}。让我们应用第五个属性来找到形数。

从给定的集合 Z 中，创建包含五个元素的子集。我们得到

{1, 2, 3, 4, 5}, {1, 2, 3, 4, 6}, {1, 2, 3, 5, 6}, {1, 2, 4, 5, 6}, {1, 3, 4, 5, 6}, {2, 3, 4, 5, 6}

从上面的子集中，确定最小的两个数字并将它们相加。即

a(6) = (1+2) + (1+2) + (1+2) + (1+2) + (1+3) + (2+3) = 21

同样，我们可以使用公式a(n) = 3*C(6+1,6)。让我们将 n=6 的值代入公式，我们得到

a(6) = 21 = 3*C(6+1,6)

让我们使用另一个公式来检查数字 84 是否为形数。

a(9) = (1, 3, 3, 1)。 (1, 6, 15, 20) = (1 + 18 + 45 + 20) = 84

因此，第 9 个形数是84。

前几个形数是

0, 0, 0, 0, 0, 0, 1, 7, 28, 84, 210, 462, 924, 1716, 3003, 5005, 8008, 12376, 18564, 27132, 38760, 54264, 74613, 100947, 134596, 177100, 230230, 296010, 376740, 475020, 593775, 736281, 906192, 1107568, 1344904, 1623160, 1947792, 2324784, 2760681, 3262623

使用差分法

我们可以使用差分法计算形数。例如，考虑以下九边形数。

但是上述方法并不总是有效。

形数类型

4 维形数 (A002417)

可以使用以下公式计算

它是 OEIS 序列A002417。

前几个4 维形数是

1, 8, 30, 80, 175, 336, 588, 960, 1485, 2200, 3146, 4368, 5915, 7840, 10200, 13056, 16473, 20520, 25270, 30800, 37191, 44528, 52900, 62400, 73125, 85176, 98658, 113680, 130355, 148800, 169136, 191488, 215985, 242760, 271950, 303696, 338143, 375440, 415740.

性质

• a(n) 是 n+2 种颜色对 2 X 2 六边形阵列进行着色的颜色数的 1/6。

• a(n) 是不能写成 t*(n+1) + u*(n+2)（其中 t, u 为非负整数）的所有数字的总和。
• a(n) 是由 n 行（或底为 2n-1）正方形组成的阶梯金字塔中包含的矩形（包括正方形）的总数。
• a(n) 等于 -1 乘以 (n + 2) X (n + 2) 矩阵的主对角线为 2，其他地方为 1 的特征多项式的 x^3 的系数。
• a(n) 是卷积数组的第 n 个反对角线和。
• 同样，也是 (n+2)-三角形图中的 3-循环数。

计算 4 维形数的公式

• 一般公式： x*(1+3*x)/(1-x)^5
• a(n) = C(n+2, 2)*n^2/3
• a(n) = C(n+3, n)*C(n+1, 1)
• a(n) = (binomial(n+3, n-1) - binomial(n+2,n-2))*(binomial(n+1,n-1) - binomial(n,n-2))
• a(n) = 5*a(n-1) -10*a(n-2) +10*a(n-3) -5*a(n-4) +a(n-5)，n>5
• a(n) = A080852(4, n-1)
• a(n) = A000332(n+3) + 3*A000332(n+2)

4 维形数 (A002418)

还有另一个计算4 维形数的公式是

它是 OEIS 序列A002418。

序列A002418的前几个形数是

0, 1, 9, 35, 95, 210, 406, 714, 1170, 1815, 2695, 3861, 5369, 7280, 9660, 12580, 16116, 20349, 25365, 31255, 38115, 46046, 55154, 65550, 77350, 90675, 105651, 122409, 141085, 161820, 184760, 210056, 237864, 268345, 301665, 337995.

性质

• 序列A002418是 A002413 的部分和。
• 卷积数组 A213550 的主对角线，对于 n>0。
• A000027 与 A000566 的卷积。

计算 A002418 序列形数的公式

• 一般公式： x*(1+4*x)/(1-x)^5
• 指数公式： x*(24 + 84*x + 44*x^2 + 5*x^3)*exp(x)/4!

其他公式有

• a(n) = n*C((n+3),4)) - (n-1)*C((n+2),4)) 或 a(n) = A128064* A000332。
  例如，a(5) = 5*C(8,4) - 4*C(7,4) = 5*70 - 4*35 =210。
• a(0)=0, a(1)=1, a(2)=9, a(3)=35, a(4)=95 则 a(n) = 5*a(n-1) - 10*a(n-2) + 10*a(n-3) - 5*a(n-4) + a(n-5)
• a(n) = A080852(5, n-1)

4 维形数 (A002419)

还有一个计算4 维形数（序列A002419）的公式。我们可以使用以下公式计算

序列A002419的前几个形数是

1, 10, 40, 110, 245, 476, 840, 1380, 2145, 3190, 4576, 6370, 8645, 11480, 14960, 19176, 24225, 30210, 37240, 45430, 54901, 65780, 78200, 92300, 108225, 126126, 146160, 168490, 193285, 220720, 250976, 284240, 320705, 360570, 404040, 451326

性质

• a(n) 是卷积数组 A213761 的第 n 个反对角线和。
• a(n) = A016777(0) 到 A016777(n-1) 的 k 元组相加的所有方式之和。

假设我们必须计算 n=4。项是1,4,7,10，得到(1)+(4)+(7)+(10)=22； (1+4)+(4+7)+(7+10)=33； (1+4+7)+(4+7+10)=33； (1+4+7+10)=22；将 22+33+33+22 相加，我们得到110，这是一个形数。

计算 A002419 序列形数的公式

• a(n) = (3*n-1)*binomial(n+2, 3)/2
• 一般公式： x*(1+5*x)/(1-x)^5
• 指数公式： x*(12 + 48*x + 26*x^2 + 3*x^3)*exp(x)/12。
• a(n) = (3*n^4 + 8*n^3 + 3*n^2 - 2*n)/12
• a(n) = A080852(6, n-1)

规则形数 (A090466)

阶数大于 2 的 k-边形数的排序。如果包含秩 2 或 2-边形数，则每个数字都会出现。它也称为多边形数。它是 OEIS 序列A090466。

小于或等于 10^k 的项数，其中 k = 1, 2, 3, ...：3, 57, 622, 6357, 63889, 639946, 6402325, 64032121, 640349979, 6403587409, 64036148166, 640362343980，等等。

对于所有素数 p >= 5 的平方 p^2，至少存在一个 a(n) 使得p^2 = a(n) + 1。因此，秩为 3 的子集 P_s(3) 就足够了。

证明

对于p >= 5，p^2 == 1 (mod {3,4,6,8,12,24}) 并且 P_s(3) + 1 = 3*s - 2 == 1 (mod 3)。因此，集合 {p^2} 是 {P_s(3) + 1} 的子集。

对于所有素数p > 5，至少存在一个多边形数 P_s(k) + 1 = p，其中 k = 3 或 4，具体取决于 p mod 6。

数字 m，使得 r = (2*m/d - 2)/(d - 1) 是某个 d 的整数，其中 2 < d < m 是 2*m 的除数。如果 r 是整数，则 m 是第 d 个 (r+2)-边形数。

序列 A090466 的前几个数字是

6, 9, 10, 12, 15, 16, 18, 21, 22, 24, 25, 27, 28, 30, 33, 34, 35, 36, 39, 40, 42, 45, 46, 48, 49, 51, 52, 54, 55, 57, 58, 60, 63, 64, 65, 66, 69, 70, 72, 75, 76, 78, 81, 82, 84, 85, 87, 88, 90, 91, 92, 93, 94, 95, 96, 99, 100, 102, 105, 106, 108, 111, 112, 114, 115, 117, 118.

形数 Java 程序

下面的 Java 程序检查给定的数字是否为平方数。

FigurateNumberExample1.java

输出

Enter a number: 100
100.0 is a square number.

让我们创建另一个 Java 程序来处理称为九边形数的形数。

NonagonalNumberExample.java

输出

Enter the term you want to find: 4
The 4 rd/th nonagonal number is: 46