用于模式搜索的有限自动机算法

使用 有限自动机 进行模式搜索是一种 字符串匹配技术，它使用有限状态机在文本中定位模式的出现。它会预处理模式以创建转换表，从而能够使用恒定的状态转换时间来高效扫描文本。

这种方法保证了确定性和快速搜索，使其成为文本处理和计算语言学等应用的理想选择。

什么是有限自动机？

有限自动机是识别输入序列中模式的抽象机器，为理解计算机科学中的正则语言奠定了基础。自动机由几个状态和规则组成，允许它根据输入符号从一个状态转换到另一个状态。

如果机器在处理完输入后处于接受状态，则接受；否则，则拒绝。

有限自动机的关键特征

1. 输入： 传递给机器进行处理的一组字符或符号。
2. 输出： 处理完输入模式后，机器将接受或拒绝它。
3. 自动机状态： 这是机器的配置和条件。
4. 状态关系： 它显示了状态之间的转换。
5. 输出关系： 根据最终状态，做出输出决策。

有限自动机的形式化定义

有限自动机是一种可以定义为元组的机器

{Q, Σ, q, F, δ}

其中

Q： 一个有限的状态集合。

Σ： 一组输入符号。

q： 初始状态。

F： 最终状态的集合。

δ： 转换函数。

什么是模式搜索？

模式搜索，也称为模式匹配，是 计算机科学 中的一个基本主题，具有文本处理和生物信息学等多种应用。基于有限自动机的模式查找算法是解决此问题的有效方法。

用于模式搜索的有限自动机算法

输入 字符串 为 text[0….. k - 1]，模式字符串为 ptr[0…. l - 1]。我们需要开发一个函数来查找给定字符串中的模式。此 函数 将接受两个参数：char ptr[] 和 char text[]。然后该函数将返回模式字符串 ptr[] 在输入字符串 text[] 中出现的次数。我们可以假设输入字符串比模式字符串长 (k > l)。

示例

示例 1

示例 1

输入： text = “TEST SAMPLES SENT FOR TEST.”

ptr = “TEST”

输出： 在 0 处识别到模式

在 22 处识别到模式

解释

示例 2

输入： text = “PQRSPPSPTRRPPSPPSPTRQS”

ptr = “PPSP”

输出： 在 4 处识别到模式

在 11 处识别到模式

在 14 处识别到模式

解释

示例 3

输入： text = “STOPTOTTSPTO”

ptr = “PTO”

输出： 在 3 处识别到模式

在 9 处识别到模式

解释

有限自动机用于模式搜索算法的通用算法

步骤 1： 创建转换函数 (TF) 表

步骤 1.1： 转换函数 (TF) 表将根据输入符号和字母显示 DFA 状态之间的转换。

步骤 1.2： 我们可以通过遍历所有可能的州和符号来生成它，并根据当前状态和输入符号选择下一个状态。

步骤 1.3： get Next State 方法使用当前状态和输入符号来确定下一个状态。

步骤 2： DFA 遍历文本

步骤 2.1： 创建 TF 表后，我们应该在文本上遍历 DFA 以查找和匹配输入文本中模式的出现。

步骤 2.2： 我们将从初始状态（状态 0）开始，DFA 将根据文本中的字符转换到后续阶段。

步骤 2.3： 当 DFA 到达最终状态（代表模式结束）时，如果找到匹配项，则保存该出现的位置索引。

步骤 3： 打印结果

步骤 3.1： 如果在遍历过程中找到匹配项，我们应该打印出现的位置索引。

步骤 3.2： 如果未找到匹配项，我们将输出“在输入文本中未找到模式。”

有限自动机用于模式搜索算法的实现

模式匹配自动机非常高效，因为它们仅评估每个文本一次，每个文本字符花费相同的时间。因此，我们可以说字符串匹配所需的时间是 O(K)，其中 K 是文本字符串的长度。但是，预处理时间（构建有限自动机所需的时间）可能很长。

现在让我们来看一下模式 STSTSVS 的有限自动机。

上面的图表提供了模式 STSTSVS 的图形和表格表示。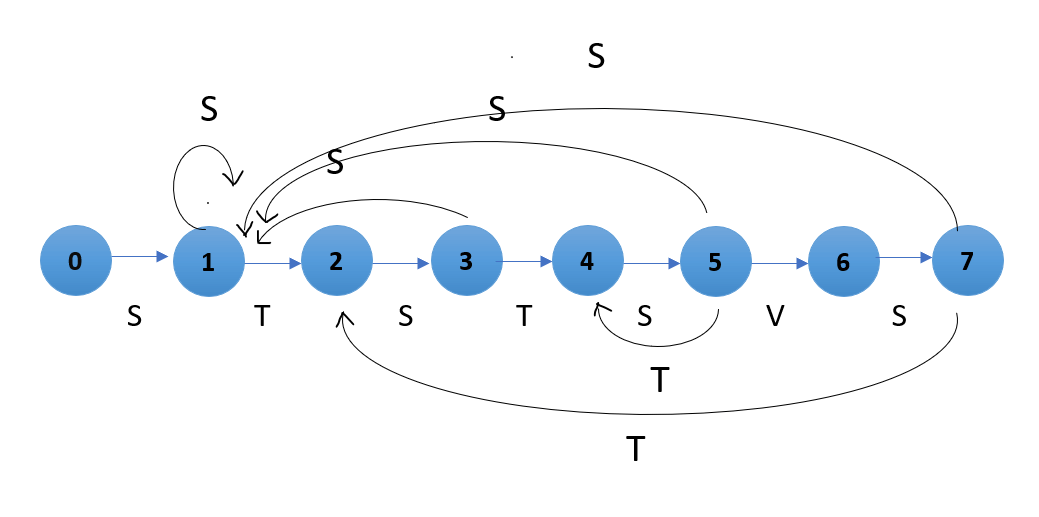

表格表示

E 表示转换函数（FA 结束）

有限自动机中的状态数将是 k+1，其中 k 是模式的长度。构建有限自动机的基本目标是确定每个可能字符从当前状态到未来状态的转换。

给定一个字符 b 和一个状态 c，我们可以通过评估字符串“ptr[0..c-1]b”来推导出下一个状态，该字符串是模式字符 ptr[0]、ptr[1] 和 ptr[c-1] 与字符 b 的简单组合。目标是确定提供的模式中最长的、作为“ptr[0..c-1]b”后缀的前缀的长度。长度值决定了下一个状态。

例如，考虑如何在上面的图中从当前状态 5 和字符 'T' 确定下一个状态。我们必须考虑字符串“ptr[0..4]S”，即“STSTST”。模式中最长的、作为“STSTST”后缀的前缀的长度是 4（“STST”）。因此，下一个状态（状态 5 之后）是字符 'T' 的 4。

上图中当前状态 5 和字符 'T'。首先，我们必须考虑字符串“ptr[0..4]T”，即“STSTST”。模式中最长的、作为“STSTST”后缀的前缀的长度是 4（“STST”）。因此，下一个状态（状态 5 之后）

在接下来的程序中，我们将创建一个函数来生成有限自动机。该函数的时间复杂度为 O(k3 * l)，其中 k 是模式字符串的长度，l 是字母表大小（给定模式和文本中所有可能的字母总数）。

该实现旨在获得所有以最长可能序列开头的缀，该序列可以是“ptr[0 … c - 1]b”的后缀。可以使用几种实现来以 O(k*l) 的时间构建有限自动机。

输出

 
The Pattern identified at the index 0
The Pattern identified at the index 8
The Pattern identified at the index 14
 
The Pattern identified at the index 6
The Pattern identified at the index 24